题解 CF1163C1 Power Transmission (Easy Edition)

传送门

题意描述

平面上有 \(n\) 个点，每两个点之间有一条直线，求有多少对直线相交。

注意：

• 若有多条直线完全重合，则他们都算是同一条一条直线；
• 求的是有多少对直线相交，而不是有多少个交点。

思路分析

一条直线可以表现为：\(y=kx+b\)。

由初中知识可得：

• 两条直线不是相交就是平行；
• 平行 \(\Leftrightarrow\) \(k\) 相等。

因此，题目就可以转化为：有多少对直线的 \(k\) 不相等。

方法解析

如何求 \(k\)

由初中知识得：

• \(k\) 即为斜率；
• 斜率 \(=\) 纵坐标之差 \(\div\) 横坐标之差。

具体地，若有两个点 \(a,b\)，则 \(k=(x_a-x_b)\div(y_a-y_b)\)。

另外，由于 \((x_a-x_b)\div(y_a-y_b)=(x_b-x_a)\div(y_b-y_a)\)，因此 \(k\) 与 \(a,b\) 两点的相对位置无关，即无需考虑 \(a,b\) 之间的位置关系，直接算就好。

接下来考虑一个问题：\(k\) 不一定是整数，而此题要求比较两个 \(k\) 是否严格相等，使用 double 大概率会碰上精度的问题—— 比如\(\frac{1}{9999}\) 与 \(\frac{1}{10000}\)，因此我们考虑以下算法：

定义两个变量 \(k\_son\) 与 \(k\_mom\)，分别表示 \(k\) 的分子与分母，那么 \(k\) 便可以表示为 \(\frac{k\_son}{k\_mom}\)，我们只要把 \(k\) 约分，那么便可以通过 \(k\_son\) 与 \(k\_mom\) 精准表示每一个 \(k\)。

---

注意点：

• 由于我们直接计算 \(k\)，可能会出现 \(k=\frac{-1}{2}\) 与 \(k=\frac{1}{-2}\) 的情况，它们两个是同一个 \(k\) 但是 \(k\_son\) 与 \(k\_mom\) 并不相等。因此我们应该维护 \(k\_mom\) 恒大于 \(0\)，这样子就不会在比较时出现问题；
• 当直线平行于 \(y\) 轴时，我们可以令 \(k\_son=1,k\_mom=0\)，与其他直线区分开来；
• 当直线平行于 \(x\) 轴时，我们应当令 \(k\_son=k\_mom=0\)，防止出现类似于 \(\frac{0}{1}\neq\frac{0}{2}\)的问题。

---

对于 \(b\)

\(b\) 能用来干什么？\(b\) 能用来判重合的直线。

由于我们能通过 \(y=kx+b\) 精准表示每一条直线，因此只要两条直线的 \(k,b\) 都相等，它们就是同一条直线。

\(b=y-kx\)，由于 \(k\) 被我们用分数表示，我们可通过先通分，再约分的流程求出 \(b\)。

但是！由于本人太菜了在写题解的时候才想到了这个方法，因此我们再说说另一个办法！

---

如何判重

显然我们可以用 \(k,b\) 判重，但是我们现在来考虑另一种做法。

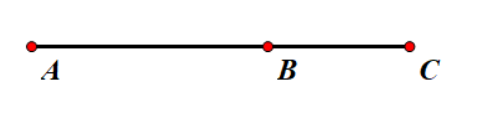
我们回到初中数学，如下图：

如何判断三点共线？

\(\because AB//BC\)

\(\therefore A,B,C\) 共线

相信你的数学老师是不会给你错的！

如果用人话讲就是：若两条平行线段有公共端点，那么它们共线。

带入到题目中，由于题目每两个点直接都连一条直线的性质，若是我们把直线变为线段，那么一条线段一定和另一条与它共线的线段有公共端点（如果有的话）。

我们定义 \(x_i, y_i\) 表示 \(i\) 号直线的两个原端点，如果有两条直线有一个原端点重合并且这两条直线平行，那么它们共线。

我们可以用dfs来解决此问题。

AC代码

说了这么多，上代码！

#include<iostream>
#include<cstdio>
#include<cmath>
#include<map>
using namespace std;

const int N = 51;
struct Node
{
    int k_mom, k_son, x, y;
}line[1000000];

struct Spot
{
    int x, y;
}a[1000000];

bool z[1000000];
int len;

int gcd(int a, int b)
{
    if(b == 0) return a;
    return gcd(b, a % b);
}

void dfs(int u)//dfs判重
{
	z[u] = true;
	for(int i = 1; i <= len; i ++)
	{
		if(!z[i] && (line[i].x == line[u].x || line[i].x == line[u].y || line[i].y == line[u].y || line[i].y == line[u].x) && line[i].k_son == line[u].k_son && line[i].k_mom == line[u].k_mom)
		{
			dfs(i);
		}
	}
}

int main()
{
    int n, x, y, x1, y1, ans = 0;
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++)
    {
        scanf("%d %d", &a[i].x, &a[i].y);
    }

    for(int i = 1; i <= n; i ++)//生成直线
    {
        if(z[i]) continue;
        for(int p = 1; p < i; p ++)
        {
            if(z[p] || (a[i].x == a[p].x && a[i].y == a[p].y)) continue;

            if(a[i].x == a[p].x)
            {
                line[++ len].k_son = 0;
                line[len].k_mom = 0;
                line[len].x = i, line[len].y = p;
            }
            else if(a[i].y == a[p].y)
            {
                line[++ len].k_son = 1;
                line[len].k_mom = 0;
                line[len].x = i, line[len].y = p;
            }
            else
            {
                x = a[i].x - a[p].x, y = a[i].y - a[p].y;
                line[ ++ len].k_son = x / gcd(abs(x), abs(y));
                line[len].k_mom = y / gcd(abs(x), abs(y));
                line[len].x = i, line[len].y = p;

				if(line[len].k_mom < 0)//维护k_mom恒大于0
				{
					line[len].k_mom *= -1;
					line[len].k_son *= -1;
				}
            }
        }
    }

    for(int i = 1; i <= len; i ++)//判重
    {
    	if(!z[i])
		{
			dfs(i);
			z[i] = false;
		}
	}
	
    for(int i = 1; i <= len; i ++)//计算答案
    {
    	if(z[i]) continue;
        for(int p = 1; p < i; p ++)
        {
        	if(z[p]) continue;
            if(line[i].k_mom != line[p].k_mom || line[i].k_son != line[p].k_son)
            {
                ans ++;
            }
        }
    }
	
    cout << ans << endl;

    return 0;
}

---

Written by \(\operatorname{Rosmarinus}\).

希望能对您有所帮助。