wqs 二分（凸完全单调性）

大学习 https://www.cnblogs.com/FloatingLife/p/19093641。

本文部分参考该博客。

前置：斜率优化。我写的

---

凸完全单调性（wqs 二分），有两个要素：凸（答案函数是凸的），完全单调（就是凸包）。

可以简单理解为降维打击（发明这词的人太伟大了）。

就是你一开始会有多维 dp，但无法优化，打表或感性理解发现 dp 值随某一维增大，呈现单调性，就可以用 wqs 二分。

---

该部分为搬运 https://www.cnblogs.com/FloatingLife/p/19093641。

假设 \(g(x)\) 图像为上凸包，此时我们要求最大值，不妨画一下 \(g(x)\) 的大致图像(当然其实我们是一个点都求不出来的)

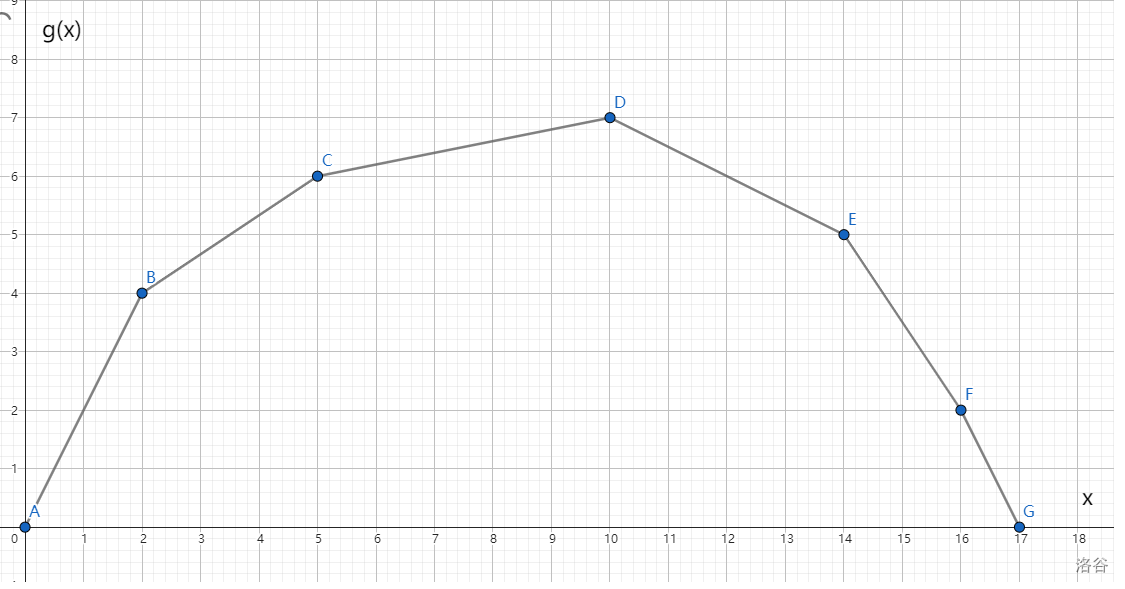
假设我们现在用一条直线 \(y=kx+b\) 去切一个点 \((x,g(x))\)，那么可以得到 \(g(x)=kx+b\)，即这个点的坐标也可以表示成 \((x,kx+b)\)。
又因为上凸包有个性质，一条斜率为 \(k\) 的直线在他与这个凸包的切点处截距最大，也就是说如果我们能求出这个最大截距，并知道此时的横坐标，就能知道那个切点的具体坐标了。
因为凸包的斜率是单调的，所以随着 \(k\) 的减小，切到的 \(x\) 也越大，所以可以二分这个 \(k\)，然后根据切点的坐标去调整 \(k\) 直到切到 \((m,g(m))\) 为止。

现在的问题就是怎么求最大截距，因为我们压根不知道这个凸包长什么样子。
会发现 \(b=g(x)−kx\)，定义截距函数 \(h(x)=g(x)−kx\)，如果我们能以较低的复杂度求出最大的 \(h(x)\) 以及此时的 \(x\)，也就求出了我们要的东西。
考虑给 \(h(x)\) 定义一个合理的意义，不难发现他其实就是给每个物品多加了一个 \(−k\) 的权值，选了这个物品就要 \(−k\)。
而我们要求 \(h(x)\) 的最大值是没有限制要选多少个的，所以 DP 时只需要设一维即可，会更好求，具体的优化方法/求法因题目而异，在例题中会讲。
注意最后求 \(g(x)\) 时，要记得把 \(kx\) 加上。

实现细节——共线情形

当凸包上存在多个点共线的时候，我们二分的直线可能会同时切到很多点，如果我们最后求出来的 \((x,h(x))\) 是从中任取一个的话，会使得我们可能漏掉最终答案的位置。因此我们需要保证每次求出来的切点是所有可行切点中横坐标最小/最大的。
这是 wqs 二分最容易出错的点，在之后的例题中也会额外注明。

由于相邻两点的横坐标之差是 \(1\)，所以此时斜率和差分没有区别，而当 \(g(x)\) 一定是整数时，斜率也一定是整数，因此我们二分也只需要二分整数域就一定可以切到要求的点；而当最后的答案可能是小数时，我们二分的斜率也应是实数域。

假设我们最终二分出来的斜率为 \(k\)，在 check 函数里求出来的是 \((x,h(x))\)，那么假设我们在共线的时候取的是 \(x\) 最小的，则我们只能保证 \(x\le m\)，即 \(x\) 不一定恰好就是 \(m\)，但是我们可以知道用斜率为 \(k\) 的线去切，切在 \(x\) 上和切在 m 上的截距都是 \(h(x)\)，因此最后的答案是 \(h(x)+km\)，而不是 \(h(x)+kx\)。

---

练习题：（继续试点）

P5896 [IOI 2016] aliens

我们先参考 P2900 [USACO08MAR] Land Acquisition G 一类思想，先把选上一定不优的点扔走。

例如下图，显然我们扔掉所有蓝点对答案不会产生影响，先扔掉。

再考虑 \(O(n^2m)\) 的 dp，使用斜率优化即可做到 \(O(nm)\)。

答案即为 \(\min (dp[n][i]) ,i \in [1,m]\)。

发现卡在 \(O(nm)\) 上了。

感性理解容易发现，函数 \(f(k)=dp[n][k]\) 是个上凸包。

简单思考，发现多分出一个正方形一定不会比不分出劣，所以 \(f(k)\) 图像是个上凸包。

答案即为 \(\min (dp[n][i]) = dp[n][m]\)。

直接起手 wqs 二分，采用上面 \(h(x)\) 的策略和意义进行二分即可。

来推一下一维 dp 方程：

令 \(g_i=(\max(0,y_i-x_{i+1}+1))^2\)。

则 \(dp_i=dp_j+(y_i-x_{j+1}+1)^2-g_j\)。

令 \(y_i+1 \to y_i\)。

则方程变为：

\(g_i=(\max(0,y_i-x_{i+1}))^2\)

\(dp_i=dp_j+(y_i-x_{j+1})^2-g_j\)

\[\begin{equation*} \begin{aligned} dp_i&=dp_j+(y_i-x_{j+1})^2-g_j\\ &=dp_j+(y_i)^2-2\times y_i \times x_{j+1}+ (x_{j+1})^2-g_j\\ &=dp_j+(y_i)^2-x_{j+1}\times 2y_i+ (x_{j+1})^2-g_j\\ \end{aligned} \end{equation*}\]

将方程化为 \(y=kx+b\) 的形式。

\[dp_j+(x_{j+1})^2-g_j=y_i\times 2x_{j+1}+dp_i+(y_i)^2 \]

其中

\[\begin{equation*} \begin{aligned} &k=y_i\\ &x=2x_{j+1}\\ &y=dp_j+(x_{j+1})^2-g_j\\ &b=dp_i+(y_i)^2\\ \end{aligned} \end{equation*}\]

要求最小化 \(dp_i\)，即最小化截距 \(b\)，发现可以单调队列维护一个下凸包，和斜率优化一样套路，队头为最优决策点。

注意本题凸包长这样，二分斜率时斜率必须是非正数。即 \(k \in [-1\times 10^{18},0]\)

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar()                                                              \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt)     \
	? EOF                                                                 \
	: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
	int x=0,c=getchar(),f=0;
	for(;c>'9'||c<'0';f=c=='-',c=getchar());
	for(;c>='0'&&c<='9';c=getchar())
		x=(x<<1)+(x<<3)+(c^48);
	return f?-x:x;
}
inline void write(int x)
{
	if(x<0) x=-x,putchar('-');
	if(x>9)  write(x/10);
	putchar(x%10+'0');
}

#ifndef ONLINE_JUDGE
#define ONLINE_JUDGE
#endif

int n,m,k;
struct Node{
	int x,y;
}a[1<<20],b[1<<20];
// int cnt;
bool cmp(Node x,Node y) { return x.x<y.x||(x.x==y.x&&x.y>y.y); }

int dp[1<<20],cnt[1<<20];
int head,tail,q[1<<20];
int g[1<<20];

void clear()
{
	head=1;
	tail=0;
	for(int i=0;i<=n;i++)
	{
		dp[i]=0;
		cnt[i]=0;
		q[i]=0;
	}
}


// int sq(int x) {return x*x;}
// int Y(int i) {return dp[i]+sq(p[i+1].x)-g[i]-K;}

inline int Y(int i)
{
	return dp[i]-g[i]+(a[i+1].x*a[i+1].x);
}

inline int X(int i) { return 2*a[i+1].x; }

inline long double slope(int i,int j)
{
	return (long double)1.0 *(Y(i)-Y(j))/(X(i)-X(j));
}

const long double eps=1e-9;

int check(int k)
{	
	clear();
	q[++tail]=0;
	for(int i=1;i<=n;i++)
	{
		while(head<tail&&slope(q[head],q[head+1])<a[i].y) head++;
		while(head<tail&&abs(slope(q[head],q[head+1])-a[i].y)<eps&&cnt[q[head]]>cnt[q[head+1]]) head++;

		dp[i]=(a[i].y-a[q[head]+1].x)*(a[i].y-a[q[head]+1].x)+dp[q[head]]-g[q[head]]-k;
		cnt[i]=cnt[q[head]]+1;

		while(head<tail&&slope(q[tail],i)<slope(q[tail],q[tail-1])) tail--;
		while(head<tail&&abs(slope(q[tail],i)-slope(q[tail],q[tail-1]))<=eps&&cnt[q[tail]]>=cnt[i]) tail--;
		
		q[++tail]=i;;
	}
	return cnt[n];
}

signed main()
{
	#ifndef ONLINE_JUDGE
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	#endif

	n=read();
	m=read();
	k=read();
	for(int i=1;i<=n;i++)
	{
		int x=read(),y=read();
		x++;
		y++;
		if(x>y) swap(x,y);
		a[i]={x,y};
	}
	int nw=0,cnt=0;
	sort(a+1,a+1+n,cmp);
	for(int i=1;i<=n;i++)
	{
		if(a[i].y<=nw) continue;
		b[++cnt]=a[i];
		nw=a[i].y;
	}
	swap(a,b);
	swap(cnt,n);
    sort(a+1,a+1+n,cmp);
	for(int i=1;i<n;i++) 
		if(a[i+1].x<=a[i].y) g[i]=(-a[i+1].x+a[i].y+1)*(-a[i+1].x+a[i].y+1);
	
	for(int i=1;i<=n;i++) a[i].y++;

	int l=-1e18,r=0,mid=0,ans=0;
	while(l<=r)
	{
		mid=(l+r)>>1;
		if(check(mid)>k) r=mid-1;
		else ans=mid,l=mid+1;
	}
	check(ans);
	cout<<dp[n]+ans*k<<"\n";

	return 0;
}