CSP-S模拟33
CSP-S模拟33
A. Divisors (div)
给定 \(m\) 个不同的正整数 \(a_1,a_2,\dots a_m\),请对 \(0\) 到 \(m\) 每一个 \(k\) 计算,在区间 \([1,n]\) 里有多少正整数是 \(a\) 中恰好 \(k\) 个数的约数。
签到题。直接暴力分解因数然后统计答案即可。注意不要算入 \(> n\) 的因数。
Code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar() \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt) \
? EOF \
: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
inline void write(int x)
{
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
// #ifndef ONLINE_JUDGE
// #define ONLINE_JUDGE
// #endif
int n,m;
int a[1<<20];
unordered_map<int,int> mp;
vector<int> ans;
void chai(int x)
{
for(int i=1;i*i<=x;i++)
{
if(x%i==0)
{
mp[i]++;
if(mp[i]==1) ans.push_back(i);
if(i*i==x) break;
mp[x/i]++;
if(mp[x/i]==1) ans.push_back(x/i);
}
}
}
int cnt[1005];
signed main()
{
// #ifndef ONLINE_JUDGE
freopen("div.in","r",stdin);
freopen("div.out","w",stdout);
n=read();
m=read();
for(int i=1;i<=m;i++) a[i]=read(),chai(a[i]);
sort(ans.begin(),ans.end());
cnt[0]=n;
for(int i:ans)
{
if(i>n) break;
cnt[mp[i]]++;
cnt[0]--;
}
for(int i=0;i<=m;i++)
cout<<cnt[i]<<"\n";
// #endif
//mt19937_64 myrand(time(0));
return 0;
}
B. Market (market)
发现容量很大,价值很小,考虑经典互换维度设 \(dp[i]\) 表示选出价值为 \(i\) 的物品所需要的最小容量。
设物品体积为 \(v\),价值为 \(w\)。
初始化 \(dp[0]=0,dp[i]=inf\)。
发现 \(s=\sum{w} \le 300^2\),直接暴力转移 dp 数组 \(dp[i]=min(dp[i],dp[i-w]+v) , i \in [w,s]\) 即可。
考虑查询怎么做。
我们肯定先离线,先将物品和询问按照出现时间由小到大排序。
依次遍历每个询问,把所有出现时间 \(\le\) 当前时间而且没 dp 过的物品进行 dp。并同时累加 \(s\)。
dp 部分最劣时间复杂度 \(O(\sum_{i=1}^{300} i \times 300 ) = O(300^3)\),可以通过。
查询我们需要快速找到从大到小的第一个 \(dp[i]\) 使 \(dp[i]\le n\),\(n\) 为当前询问背包容量。
随便做即可。我考虑分块。
具体地,设块长为 \(len=300\),对每个块开一个 multiset,初始时把每个块的 dp 值插进每个块的 multiset 中。
转移时若 \(dp[i]>dp[i-w]+v\),则在 \(i\) 块所在的 multiset 中删除一个 \(dp[i]\) 并加入一个 \(dp[i-w]+v\)。
查询时下标从大到小遍历每个块,若这个块的 multiset 的第一个元素 \(\le n\),那么下标从大到小遍历这个块,遇到的第一个 \(dp[i]\le n\) 即为答案。
需要判断一个物品都买不了即答案为 \(0\) 的情况。
Code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar() \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt) \
? EOF \
: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
inline void write(int x)
{
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
// #ifndef ONLINE_JUDGE
// #define ONLINE_JUDGE
// #endif
int n,m;
struct Node{
int c,v,t;
}a[1<<20];
bool cmp(Node x,Node y) { return x.t<y.t; }
struct Ask{
int t,m,id;
}q[1<<20];
bool cmp2(Ask x,Ask y) { return x.t<y.t; }
int ans[1<<20];
int dp[1<<20];
const int len=300;
int id[1<<20];
int minn[1<<20];
// vector<int> V;
const int M=305*305,inf=0x3f3f3f3f3f3f3f3f;
multiset<int> s[M/len+10];
void add(int c,int v,int maxn)
{
// V.clear();
for(int i=maxn;i>=v;i--)
{
if(dp[i-v]+c<dp[i])
{
s[id[i]].erase(s[id[i]].find(dp[i]));
dp[i]=dp[i-v]+c;
// V.push_back(i);
// cout<<i<<" "<<dp[i]<<"\n";
minn[id[i]]=min(minn[id[i]],dp[i]);
s[id[i]].insert(dp[i]);
}
// dp[i]=min(dp[i],dp[i-v]+c);
}
}
int query2(int l,int r,int c)
{
for(int i=r;i>=l;i--)
if(dp[i]<=c) return i;
return -1;
}
int query(int c,int maxn)
{
for(int i=id[maxn];i>=1;i--)
{
// cout<<"qid="<<i<<" minn="<<(*s[i].begin())<<"\n";
if(minn[i]<=c)
{
return query2(max(1ll,(i-1)*len),min(maxn,i*len-1),c);
}
}
return 0;
}
signed main()
{
// #ifndef ONLINE_JUDGE
freopen("market.in","r",stdin);
freopen("market.out","w",stdout);
n=read();
m=read();
int maxn=0;
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<=n;i++)
{
a[i].c=read();
a[i].v=read();
a[i].t=read();
maxn+=a[i].v;
}
for(int i=1;i<=m;i++)
{
q[i].t=read();
q[i].m=read();
q[i].id=i;
}
sort(a+1,a+1+n,cmp);
sort(q+1,q+1+m,cmp2);
// cout<<maxn<<"\n";
// return 0;
memset(minn,0x3f,sizeof(minn));
for(int i=1;i<=maxn;i++) id[i]=i/len+1;
s[0].insert(0);
for(int i=1;i<=maxn;i++) s[id[i]].insert(inf);
maxn=0;
int nw=1;
for(int i=1;i<=m;i++)
{
// cerr<<i<<"\n";
while(nw<=n&&a[nw].t<=q[i].t)
{
maxn+=a[nw].v;
add(a[nw].c,a[nw].v,maxn);
nw++;
// cout<<"\n\n---------------------\n\n";
}
// cout<<"maxn="<<maxn<<"\n";
// for(int j=1;j<=maxn;j++) cout<<dp[j]<<" ";
// cout<<"\n";
ans[q[i].id]=query(q[i].m,maxn);
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<"\n";
}
// #endif
//mt19937_64 myrand(time(0));
return 0;
}
C. 连通性 (connect)
研究一下。
Code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar() \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt) \
? EOF \
: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
inline void write(int x)
{
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
#ifndef ONLINE_JUDGE
#define ONLINE_JUDGE
#endif
const int N=105;
int f[N][N][N],g[N][N],s[N];
const int mod=1e9+7;
map<pair<int,int>,int> w;
int C[N][N];
int CC(int n,int m) { return C[n][m]; }
int ksm(int x,int p)
{
int ans=1;
while(p)
{
if(p&1) ans=ans*x%mod;
x=x*x%mod;
p>>=1;
}
return ans;
}
signed main()
{
freopen("connect.in","r",stdin);
freopen("connect.out","w",stdout);
int T=read();
int n=100;
g[1][1]=s[1]=1;
s[0]=1;
C[0][0]=1;
for(int i=1;i<=n;i++)
{
C[i][0]=1;
for(int j=1;j<=n;j++)
{
C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
}
}
for(int i=2;i<=n;i++)
{
g[i][i]=g[i][1]=1;
s[i]=2;
for(int j=2;j<i;j++)
{
g[i][j]=(g[i-1][j]*j+g[i-1][j-1])%mod;
s[i]=(s[i]+g[i][j])%mod;
}
}
for(int i=1;i<=n;i++)
{
for(int t=0;t<=n-i;t++)
for(int j=2;j<=i;j++)
{
int nw=0;
for(int k=1;k<=i;k++)
for(int q=0;q<=t;q++)
{
nw=(nw+CC(i-1,k-1)*CC(t,q)%mod*f[i-k][j-1][t-q]%mod*f[k][1][q])%mod;
}
f[i][j][t]=nw;
}
f[i][1][0]=ksm(2,i*(i-1)/2);
for(int j=2;j<=i;j++) f[i][1][0]=(f[i][1][0]-f[i][j][0]+mod)%mod;
for(int t=1;t<=n;t++) f[i][1][t]=f[i][1][0]*ksm(2,t*(t-1)/2)%mod*ksm(ksm(2,i)-1,t)%mod;
}
while(T--)
{
int n=read();
int m=read();
int ans=0;
if(n==m)
{
for(int i=1;i<=n;i++) ans+=g[n][i];
cout<<ans%mod<<"\n";
}
else
{
for(int i=1;i<=n-m;i++)
for(int t=0;t<=m;t++)
ans=(CC(m,t)*s[m-t]%mod*f[n-m][i][t]%mod+ans)%mod;
cout<<ans<<"\n";
}
}
//mt19937_64 myrand(time(0));
return 0;
}
D. 树 (usmjer)
非常奇怪的一个做法。
先考虑链的情况。
下文的一个区间指一条 \(u \to v\) 的路径。
设极长有交区间为一组区间,其中的每个区间形如 \([l_i,r_i]\)。那么这组区间的极长有交区间即为 \([L=min{l_1,\dots,l_n},R=max{r_1,\dots,r_n}]\),满足若对所有 \(p \in [L,R-1] 且 \exists p \in [l_i,r_i-1]\) 连无向边 \((p,p+1)\),则该图为一个无向联通图。
画图理解

显然每个极长有交区间互不干扰。
考虑一个极长有交区间,怎么做。
发现如果我们钦定任意一条边的方向,那么这个极长有交区间所包含的所有区间的方向就确定了。
而且钦定方向向左或向右均可。
我们直接将结论上树。
尝试每遇到一条边,我们就给它钦定方向,遇到矛盾返回无解。
发现 \(\text{CH}_4\) 了,如图。你如果先钦定边 \(1\) 和 \(2\),再判断边 \(3\),就有可能被判定无解了。但实际上是有解的。
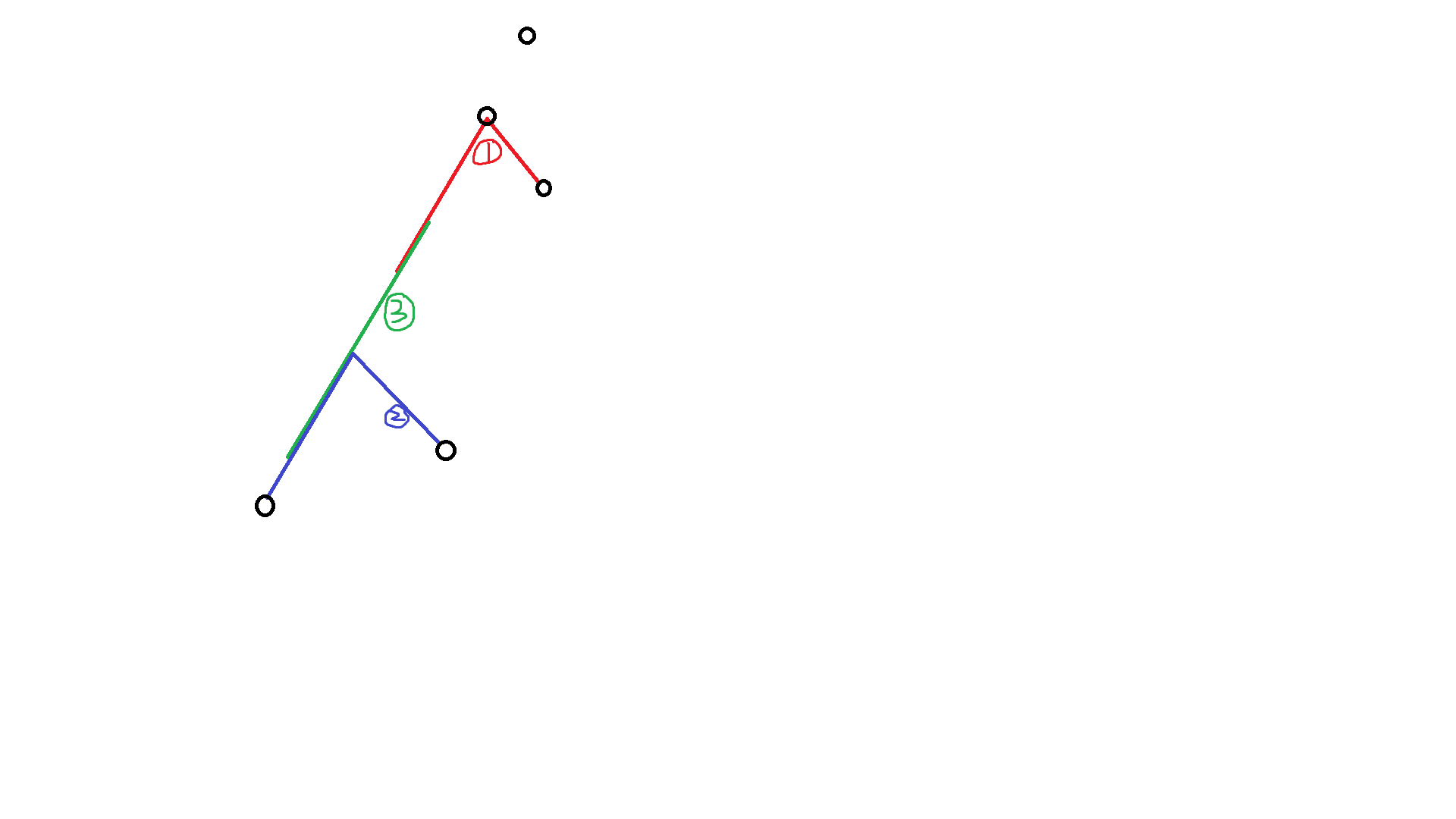
考虑修正。
我们发现,如果在一条路径的 lca 处钦定这条路径的方向,问题就会得到完美解决。
先将边的方向下放到儿子节点上(边化点)。
具体实现时从根开始 dfs,对于每个点 \(p\) 将 lca 为 \(p\) 的路径定向(注意:不包括 lca,因为边的方向被下放了),如果 \(u \to lca ,v \to lca\) 路径上有边被定向了,当且仅当这两条路径方向相同时,答案为 \(0\)。否则先满足路径上已有的方向限制对这 \(u \to v\) 的路径定向。
如果没有任何一条边被定向则将这条边随便钦定一个方向,同时 \(++cnt\)(新加一个极长有交区间)。
最后答案即为 \(2\) 的 \((\)极长有交区间的数量\(+\)所有没被定向的边数量\()\) 次幂。
发现这样做是 \(O(n^2)\) 的。考虑优化。
发现我们可以用(树上)并查集来维护跳 \(u \to lca ,v \to lca\) 的过程。直接在并查集上暴力跳 \(p=find(fa[p])\),同时查询 \(p\) 点所对应的边是否有方向即可。跳完钦定 \(p\) 点所对应的边的方向,然后令 \(bcj[p]=find(fa[p])\) 即可。
具体实现是最好先将所有 $u \to lca $ 的路径上需要定向的边(下放到的点),\(v \to lca\) 的路径上需要定向的边放进两个 vector 里,最后一起定向比较方便。也很好判无解情况。注意 vector 为空的情况。
这样每个点只会被定向一次,并查集也只会更改 \(n\) 次,\(n\) 次之后并查集内的值就全为 \(1\) 了。于是复杂度就正确了。
你极限调完发现他有 \(96 pts\) 被 Hack 了。
然后我们数据点分治即可通过本题。直观感觉应该是根节点 \(1\) 处理出锅了。
Code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar() \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt) \
? EOF \
: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
inline void write(int x)
{
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
// #ifndef ONLINE_JUDGE
// #define ONLINE_JUDGE
// #endif
const int mod=1e9+7,N=3e5+5;
int n,m;
vector<int> E[N];
int dep[N],f[N],top[N],son[N],siz[N];
void dfs1(int p,int fa)
{
siz[p]=1;
f[p]=fa;
dep[p]=dep[fa]+1;
for(int to:E[p])
{
if(to==fa) continue;
dfs1(to,p);
siz[p]+=siz[to];
if(siz[to]>siz[son[p]]) son[p]=to;
}
}
void dfs2(int p,int tp)
{
top[p]=tp;
if(son[p]) dfs2(son[p],tp);
for(int to:E[p])
if(!top[to]) dfs2(to,to);
}
int lca(int u,int v)
{
while(top[u]!=top[v])
{
if(dep[top[v]]>dep[top[u]]) swap(u,v);
u=f[top[u]];
}
return dep[u]<dep[v]?u:v;
}
struct Edge{
int u,v,lca;
};
vector<Edge> v[N];
int ans=1;
int col=0;
int tot=0;
int bcj[1<<20];
int find(int x)
{
if(x==bcj[x]) return x;
return bcj[x]=find(bcj[x]);
}
vector<int> v1,v2;
struct Point{
int col,direct;
}p[N];
int vis[N];
void work(int u,int v,int lca)
{
// cout<<u<<" -> "<<v<<" Lca="<<lca<<"\n";
v1.clear();
v2.clear();
if(u==lca)
{
v=find(v);
while(dep[v]>dep[u])
{
v1.push_back(v);
v=find(f[v]);
}
if(v1.empty()) return;
int last=v1[v1.size()-1];
if(f[last]!=lca&&vis[f[last]])
{
for(int i:v1)
{
bcj[i]=find(f[last]);
vis[i]=1;
p[i]=p[f[last]];
}
}
else
{
col++;
for(int i:v1)
{
bcj[i]=find(f[last]);
vis[i]=1;
p[i]={col,1};
}
}
// return;
}
else
{
int vv=v,uu=u;
u=find(u);
while(dep[u]>dep[lca])
{
v1.push_back(u);
u=find(f[u]);
}
v=find(v);
while(dep[v]>dep[lca])
{
v2.push_back(v);
v=find(f[v]);
}
int ud=0,vd=0,uc=0,vc=0,last1=uu,last2=vv;
if(v1.empty()) ud=p[uu].direct,uc=p[uu].col;
else
{
int last=v1[v1.size()-1];
last1=last;
if(f[last]!=lca&&vis[f[last]]) ud=p[f[last]].direct,uc=p[f[last]].col;
else ud=0;
}
if(v2.empty()) vd=p[vv].direct,vc=p[vv].col;
else
{
int last=v2[v2.size()-1];
last2=last;
if(f[last]!=lca&&vis[f[last]]) vd=p[f[last]].direct,vc=p[f[last]].col;
else vd=0;
}
// cout<<v1.size()<<" "<<v2.size()<<"\n";
if(ud!=0&&vd!=0&&ud==vd) { cout<<"0"; exit(0); }
else if(ud!=0)
{
vd=-ud;
vc=uc;
}
else if(vd!=0)
{
ud=-vd;
uc=vc;
}
else
{
col++;
vc=uc=col;
ud=1;
vd=-1;
}
for(int i:v1)
{
bcj[i]=find(f[last1]);
vis[i]=1;
p[i]={uc,ud};
}
for(int i:v2)
{
bcj[i]=find(f[last2]);
vis[i]=1;
p[i]={vc,vd};
}
}
// for(int i=2;i<=n;i++)
// {
// cout<<"p="<<i<<" col="<<p[i].col<<" dir="<<p[i].direct<<" bcj="<<bcj[i]<<"\n";
// }
// cout<<"\n";
}
void dfs3(int p,int fa)
{
for(Edge nw:v[p])
work(nw.u,nw.v,nw.lca);
for(int to:E[p])
{
if(to==fa) continue;
dfs3(to,p);
}
}
signed main()
{
// #ifndef ONLINE_JUDGE
freopen("usmjer.in","r",stdin);
freopen("usmjer.out","w",stdout);
n=read();
m=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
E[u].push_back(v);
E[v].push_back(u);
}
for(int i=1;i<=n;i++) bcj[i]=i;
dfs1(1,0);
dfs2(1,1);
// return 0;
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),Lca=lca(x,y);
if(dep[y]<dep[x]) swap(x,y);
v[Lca].push_back({x,y,Lca});
}
dfs3(1,0);
int cnt=0;
for(int i=2;i<=n;i++) col+=vis[i]==0;
int ans=1;
for(int i=1;i<=col;i++) ans=(ans*2)%mod;
if(ans==813295338) ans>>=1;
cout<<ans<<"\n";
return 0;
}
以下是博客签名,正文无关
本文来自博客园,作者:Wy_x,转载请在文首注明原文链接:https://www.cnblogs.com/Wy-x/p/19148454
版权声明:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC-BY-NC-SA 4.0 协议)进行许可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号