三期集训日记？

9.8

模拟赛。十五分钟写完 T1，后面罚坐。

下午图论专题。

CF521E Cycling City

Solution

思维好题。

首先发现，如果有三条路径，那么这些路径一定在一个双联通分量里，而且这个双联通分量不是一个环。这是做法一。

有更简洁的做法。

引理：无向图的 dfs 树上只存在树边和返祖边。

首先先把这个图的 dfs 树建出来。

发现这是个树上链覆盖状物问题。

先把边拍到儿子节点上。

考虑什么时候答案合法。发现当有一条链被覆盖两次时，一定会有答案。

考虑以下情况，其中 $S$ 与 $T$ 为合法解。

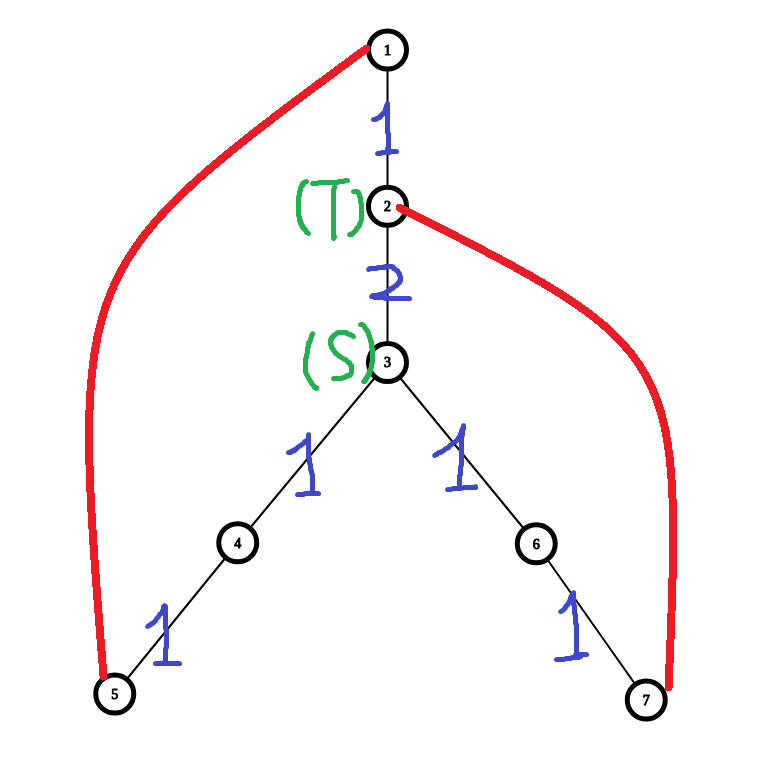
手模一下，答案就清楚了：找到最长的被覆盖两次的原树上的链，那么两头分别为 $S$ 和 $T$ 即可。注意 $i$ 的父亲也被覆盖了两次。

首先，对非树边进行链覆盖。

若现在是第一次覆盖，那么在被覆盖的边上记录这条非树边是哪一条边。

当有一条边被覆盖两次时，意味着现在有合法解了。显然这个解可以仅由现在枚举的这条非树边和以前记录的那一条覆盖了这条边的非树边得来。

那么这道题做法就显然了。

先重新用这两条非树边把原树覆盖一下。

枚举点 $i \in [1,n]$，如果 $i$ 所记录的边被覆盖两次，那么这个点就可能是 $S$ 或 $T$。

取这些点中深度最大和深度最小的点作为 $S$ 和 $T$ 即可。

然后树上 $S$ 到 $T$ 的路径为第一组合法解。

经过第一条非树边为第二组合法解。

经过第二条非树边为第三组合法解。

考虑经过非树边的路径怎么输出。令 $u$ 为这条非树边深度较小的端点。

如图，做法就显然了，分图中所示的三个步骤统计即可。

PS：若无解，每条链最多被覆盖一次，暴力跳 fa 暴力做链覆盖即可。

时间复杂度 $O(m)$。

Code

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar()                                                              \
(s == ss && (s=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == s)     \
	? EOF                                                                 \
	: *ss++)
char In[1<<20],*ss=In,*s=In;
inline int read()
{
	int x=0,c=getchar(),f=0;
	for(;c>'9'||c<'0';f=c=='-',c=getchar());
	for(;c>='0'&&c<='9';c=getchar())
		x=(x<<1)+(x<<3)+(c^48);
	return f?-x:x;
}
inline void write(int x)
{
	if(x<0) x=-x,putchar('-');
	if(x>9)  write(x/10);
	putchar(x%10+'0');
}

const int N=2e5+5;
int n,m,u[N],v[N],dep[N],f[N],id[N],cnt[N];
vector<int> G[N];
bool vis[N];

void dfs1(int p) // 建 dfs 树
{
    for(int to:G[p])
    {
        if(!vis[to])
        {
            vis[to]=1;
            f[to]=p;
            dep[to]=dep[p]+1;
            dfs1(to);
        }
    }
}

void up2(int u,int v) // 重新对两条非树边进行链覆盖
{
    while(u!=v)
    {
        if(dep[u]<dep[v]) swap(u,v);
        cnt[u]++;
        u=f[u];
    }
}

void output(int id1,int id2) // 输出答案
{
    up2(u[id1],v[id1]);
    up2(u[id2],v[id2]);
    int t=0,s=0;
    for(int i=1;i<=n;i++) // 找起点和终点
    if(cnt[i]==2)
    {
        if(t==0||dep[t]>dep[f[i]]) t=f[i]; // 因为边权化点权，所以深度最小点是 fa[i]
        if(s==0||dep[s]<dep[i]) s=i;
    }
    cout<<"YES\n";

    // 令 s 为深度较大点，t 为深度较小点

/*  ----------------------------------------------  */    
    
    // 第一条路径：s -> t
    cout<<dep[s]-dep[t]+1<<" "; 
    int nw=s;
    while(nw!=t)
    {
        cout<<nw<<" ";
        nw=f[nw];
    }
    cout<<nw<<"\n";
    
/*  ----------------------------------------------  */      
    
    // 第二条路径：t -> u1 -> v1 -> s
    // 注意：记录的路径是反的！

    vector<int> vec;

    nw=t;
    vec.push_back(nw);
    while(nw!=u[id1]) // t -> u1
    {
        nw=f[nw];
        vec.push_back(nw);
    }
    nw=v[id1]; // u1 -> v1
    vec.push_back(nw);
    while(nw!=s) // v1 -> s
    {
        nw=f[nw];
        vec.push_back(nw);
    }
    reverse(vec.begin(),vec.end()); // 翻转路径，即为所求

    cout<<vec.size()<<" ";
    for(int i:vec) cout<<i<<" ";
    cout<<"\n";

/*  ----------------------------------------------  */      
    // 第三条路径：t -> u2 -> v2 -> s
    // 注意：记录的路径是反的！

    vec.clear();
    nw=t;
    vec.push_back(nw);
    
    while(nw!=u[id2]) // t -> u2
    {
        nw=f[nw];
        vec.push_back(nw);
    }
    nw=v[id2]; // u2 -> v2
    vec.push_back(nw);
    while(nw!=s) // v2 -> s
    {
        nw=f[nw];
        vec.push_back(nw);
    }
    reverse(vec.begin(),vec.end()); // 翻转路径，即为所求
    
    cout<<vec.size()<<" ";
    for(int i:vec) cout<<i<<" ";
    cout<<"\n";
    exit(0); // 结束程序
}

void up(int u,int v,int nwid) //进行链覆盖
{
    while(u!=v)
    {
        if(dep[u]<dep[v]) swap(u,v);
        if(id[u]) { output(nwid,id[u]); exit(0); } // 被覆盖过意味着有答案，
        id[u]=nwid; // 记录被哪覆盖条边
        u=f[u];
    }
}

signed main()
{
	n=read();
    m=read();
    for(int i=1;i<=m;i++)
    {
        u[i]=read();
        v[i]=read();
        G[u[i]].push_back(v[i]);
        G[v[i]].push_back(u[i]);
    }
    for(int i=1;i<=n;i++)
    if(!vis[i]) vis[i]=1,dfs1(i);

    for(int i=1;i<=m;i++) if(dep[u[i]]>dep[v[i]]) swap(u[i],v[i]);
    // 将深度较浅的点放前面，减少码量
    for(int i=1;i<=m;i++)
    {
        if(f[v[i]]==u[i]) continue; // 跳过树边
        up(v[i],u[i],i); // 暴力覆盖非树边
    }
    cout<<"NO\n"; // 没有边被覆盖两次及以上，无解。
	return 0;
}

9.9

CF1919F2 Wine Factory (Hard Version)

Solution

显然最大流，然后尝试转最小割。

发现对于每个点 $i$，不考虑横向边，一定割 $S \to i$ 和 $ i \to T$ 其中的一条边。

横向边需要割掉，当且仅当图示情况：

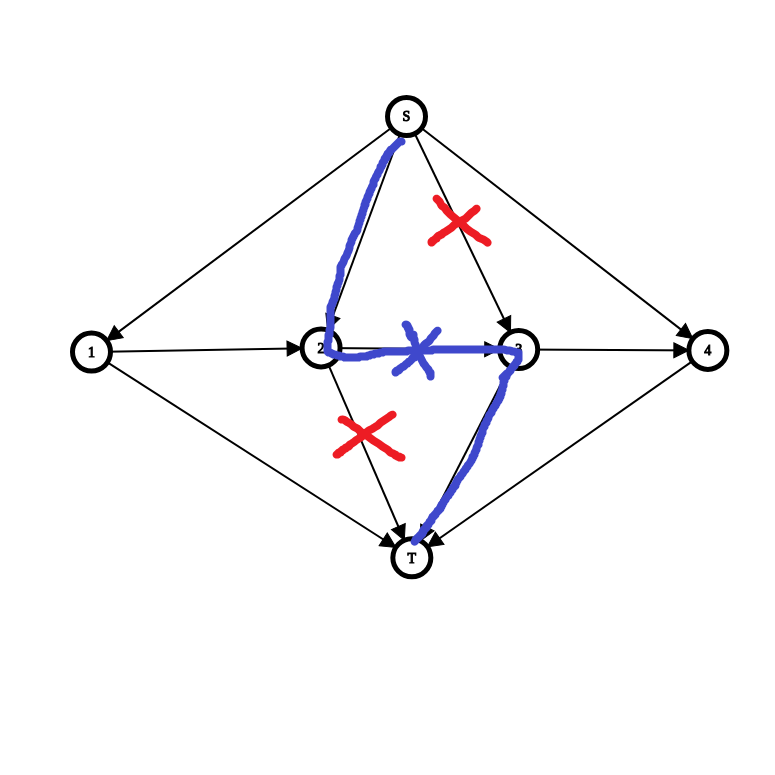
发现答案只与左右端点处的割边方案有关。这就可以拿线段树维护了。

对线段树每个节点开 $ans[0/1][0/1]$ 表示：$ans[l$ 处割 $S\to l / \ l$ 处割 $l \to T ][r$ 处割 $S\to r / \ r$ 处割 $r \to T ]$。

叶子节点赋值：

\[a[i] \to ans[0][0] \]

\[b[i] \to ans[1][1] \]

\[+inf \to ans[1][0] \]

\[+inf \to ans[0][1] \]

pushup 比较麻烦，可以自己手模。

Code

#include<bits/stdc++.h>
#define int long long
#define lp (p<<1)
#define rp ((p<<1)|1)

using namespace std;

const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar()                                                              \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt)     \
	? EOF                                                                 \
	: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
	int x=0,c=getchar(),f=0;
	for(;c>'9'||c<'0';f=c=='-',c=getchar());
	for(;c>='0'&&c<='9';c=getchar())
		x=(x<<1)+(x<<3)+(c^48);
	return f?-x:x;
}
inline void write(int x)
{
	if(x<0) x=-x,putchar('-');
	if(x>9)  write(x/10);
	putchar(x%10+'0');
}

const int N=5e5+5;
int n,q;
int a[N],b[N],c[N];
struct T{
    int ans[2][2];
}t[N<<2];

void pushup(T &p,T l,T r,int c)
{
    p.ans[0][0]=min({l.ans[0][0]+r.ans[0][0],l.ans[0][1]+r.ans[1][0],l.ans[0][0]+r.ans[1][0],l.ans[0][1]+r.ans[0][0]+c});
    p.ans[1][1]=min({l.ans[1][1]+r.ans[1][1],l.ans[1][0]+r.ans[0][1],l.ans[1][1]+r.ans[0][1]+c,l.ans[1][0]+r.ans[1][1]});

    p.ans[1][0]=min({l.ans[1][1]+r.ans[1][0],l.ans[1][0]+r.ans[0][0],l.ans[1][1]+r.ans[0][0]+c,l.ans[1][0]+r.ans[1][0]});
    p.ans[0][1]=min({l.ans[0][0]+r.ans[0][1],l.ans[0][1]+r.ans[1][1],l.ans[0][0]+r.ans[1][1],l.ans[0][1]+r.ans[0][1]+c});
}

void build(int l,int r,int p)
{
    if(l==r)
    {
        t[p].ans[0][0]=a[l];
        t[p].ans[1][1]=b[l];
        t[p].ans[0][1]=t[p].ans[1][0]=3e18;
        return; 
    }
    int mid=(l+r)>>1;
    build(l,mid,lp);
    build(mid+1,r,rp);
    pushup(t[p],t[lp],t[rp],c[mid]);
}

void change(int l,int r,int x,int p)
{
    if(l==r)
    {
        t[p].ans[0][0]=a[l];
        t[p].ans[1][1]=b[l];
        t[p].ans[0][1]=t[p].ans[1][0]=3e18;
        return;
    }
    int mid=(l+r)>>1;
    if(x<=mid) change(l,mid,x,lp);
    else change(mid+1,r,x,rp);
    pushup(t[p],t[lp],t[rp],c[mid]);
}

signed main()
{
	// freopen("dataa.in","r",stdin);
	// freopen("nw.out","w",stdout);
    n=read();
    q=read();
    for(int i=1;i<=n;i++) a[i]=read();
    for(int i=1;i<=n;i++) b[i]=read();
    for(int i=1;i<n;i++) c[i]=read();
    build(1,n,1);
    while(q--)
    {
        int p=read();
        a[p]=read();
        b[p]=read();
        c[p]=read();
        change(1,n,p,1);
        write(min({t[1].ans[0][0],t[1].ans[0][1],t[1].ans[1][0],t[1].ans[1][1]}));
        putchar('\n');
    }
    // for(int i=1;i<=n;i++) cerr<<a[i]<<" ";
    // cerr<<"\n";
    // for(int i=1;i<=n;i++) cerr<<b[i]<<" ";
    // cerr<<"\n";
    // for(int i=1;i<n;i++) cerr<<c[i]<<" ";
    // cerr<<"\n";

	return 0;
}

/*

5 1
1 1 1 2 3 
2 1 3 2 2 
1 3 3 2 
1 1 2 3
 */

$\huge{?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ }$

https://www.cnblogs.com/S-Keep-Kiding/p/19070774

作为小县城唯一玩过原神的人，我的眼神里总是透着同龄人不懂的肃穆，每次家里跳闸停电，我都会平静地抬手轻按空气开关：“巴尔泽布，此身允许你暂歇，但光明不可断绝。”
作为小县城唯一玩过原神的人，我的眼神里总带着同龄人没有的沉稳，每次看到老人在巷口摆摊卖手作小物件，我都会蹲下来轻声问：“钟离先生，您这‘契约之物’，作价几何？”
作为小县城唯一玩过原神的人，我的眼神里藏着同龄人不懂的鲜活，每次县里举办文艺汇演台下掌声雷动，我都会笑着拍手：“芙宁娜大人，这场‘审判之外的演出’，您还满意吗？”
作为小县城唯一玩过原神的人，我的眼神里总有着同龄人没有的温柔，每次在书店看到孩子捧着绘本认真阅读，我都会放轻脚步：“纳西妲，你看，智慧正在这里悄悄发芽呢。”

$\huge{?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ ?\ }$

9.10

教师节。

模拟赛。T1 假了，T2 假了，T3超级难写做法真了，T4 构造。

战绩 170 Pts。

补给大洋里十八，占了
补给大洋里十八，占了
补给大洋里十八，占了
补给大洋里十八，占了
补给大洋里十八，占了
补给大洋里十八，占了

。。。。。。。。。。

祭祭。

ctrl+D?2025-09-10 16:10:23 星期三什么编辑器自带快捷键

9.11

模拟赛。

T1 有人分讨了 18 种做法。

T2 是异或哈希状物。尝试拿乘哈希维护结果炸了

T3 简单贪心 96 Pts?

下午开心改题

（miaomiao 进来）:下午八九节补物理课啊，物理奥赛不用补，你们需要补。

于是就【】去听物理课了。

9.12

miaomiao 又在 D 我们不改题。

下午六七节于是就【】去听物理课了。

posted @ 2025-09-08 19:54 Wy_x 阅读(41) 评论(2) 收藏举报

刷新页面返回顶部

༼ つ ◕_◕ ༽つ Wy-x 的 blog 🤗

凤凰台上凤凰游，凤去台空江自流。

三期集训日记？

9.8

9.9

9.10

9.11

9.12

公告

༼ つ ◕_◕ ༽つ Wy-x 的 blog 🤗

凤凰台上凤凰游，凤去台空江自流。

三期集训 日记？

9.8

9.9

9.10

9.11

9.12

公告

三期集训日记？