插头 Dp 学习笔记
前置知识:状压 Dp。
轮廓线:

假设我们要从红点进行转移,转移到下一个点,那么绿线即为轮廓线(绿线为决策过的点与未决策过的点的分界线)。
我们可以从图中发现,轮廓线的“长度”为列数+1。
轮廓线状态为 \(s\) 时,(二进制压缩后)规定上插头为 (s>>j)&1,左插头为 (s>>(j-1))&1,四进制就是上插头为 (s>>(j*2))&3,左插头为 (s>>((j-1)*2))&3。以此类推。不用考虑边界问题,在每一行的最右边这种转移方法依旧可行。
只需要在换行时判断这一行所有的最终状态能否转移到下一行的初始状态,判断方法与状态被压进了几进制有关,思路在根本上是一样的。

转移合法的条件:转移前 \(\Large{\text{②}}\) 处不能有插头。转移后,\(\Large{\text{①}}\) 处一定没有插头。相当于把原最终状态 << 1(二进制压缩,其余进制的压缩同理)。
就是把最终状态在 x 进制下 << 1。
问题引入:P5074 Eat the Trees
吃树。
题面:给出 \(n \times m\) 的方格,有些格子不能铺线,其它格子必须铺,可以形成多个闭合回路。问有多少种铺法?
思路:简单轮廓线 Dp。设 \(dp[i][j][s]\) 表示在点 \((i,j)\) 时,轮廓线状态为 \(s\) 的方案数。
这里 s 转为二进制数后第 i 位的值表示这个位置有无插头。设有插头为 1,无插头为 0。
显然 s < (1<<(m+1)。(有 m 个上插头和 1 个左插头,一共需要 m+1 位)。
转移时讨论(有插头,在本题中指 s 的第 i 位为 1):
- 上和左均无插头。转移到下有右有。
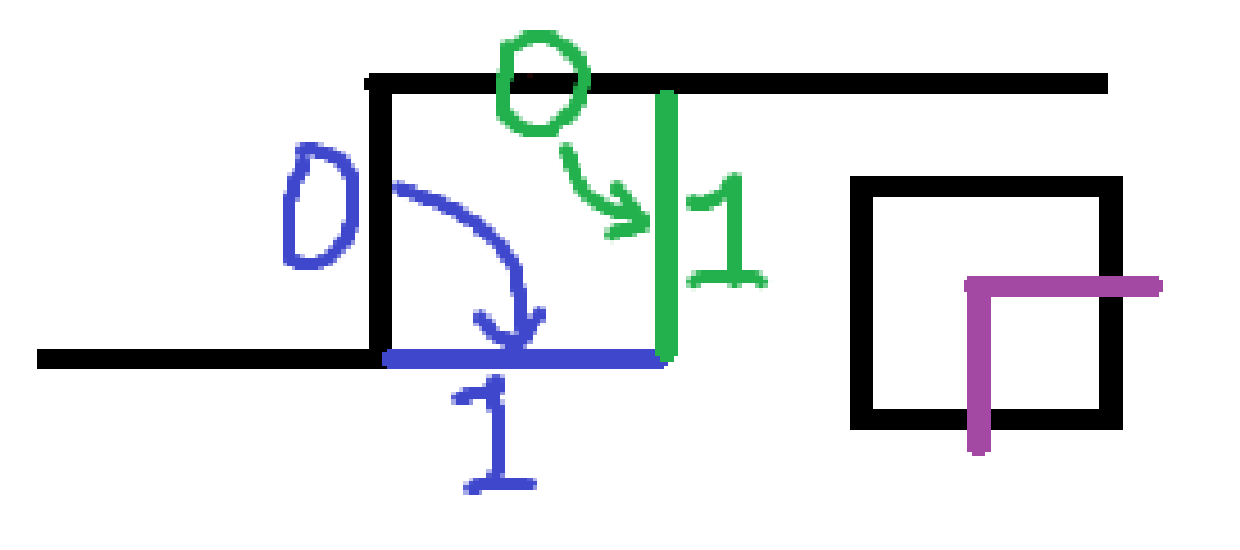
- 只有上有插头。转移到下有右无或下无右有。
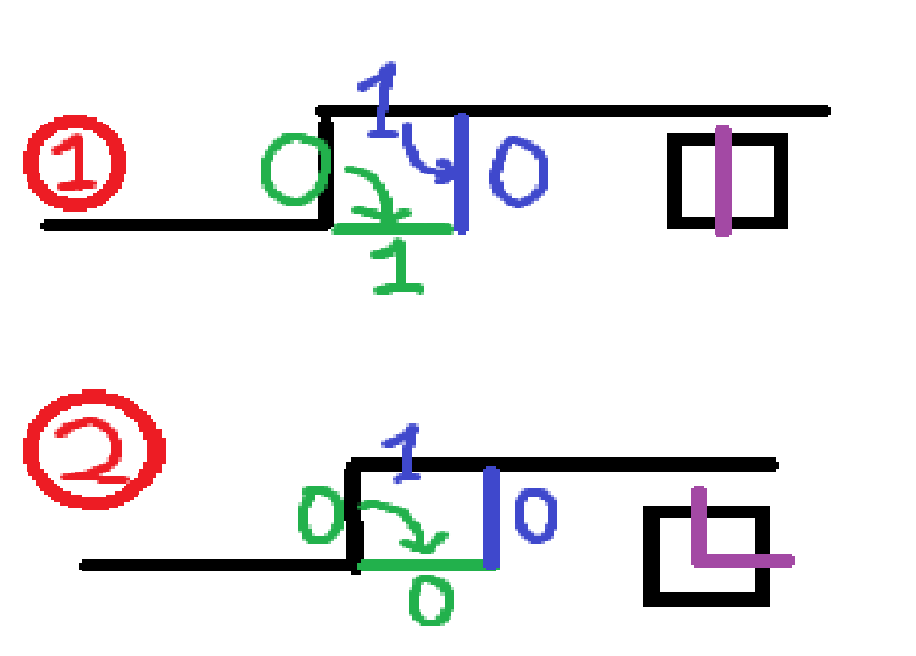
- 只有左有插头。转移到下有右无或下无右有。
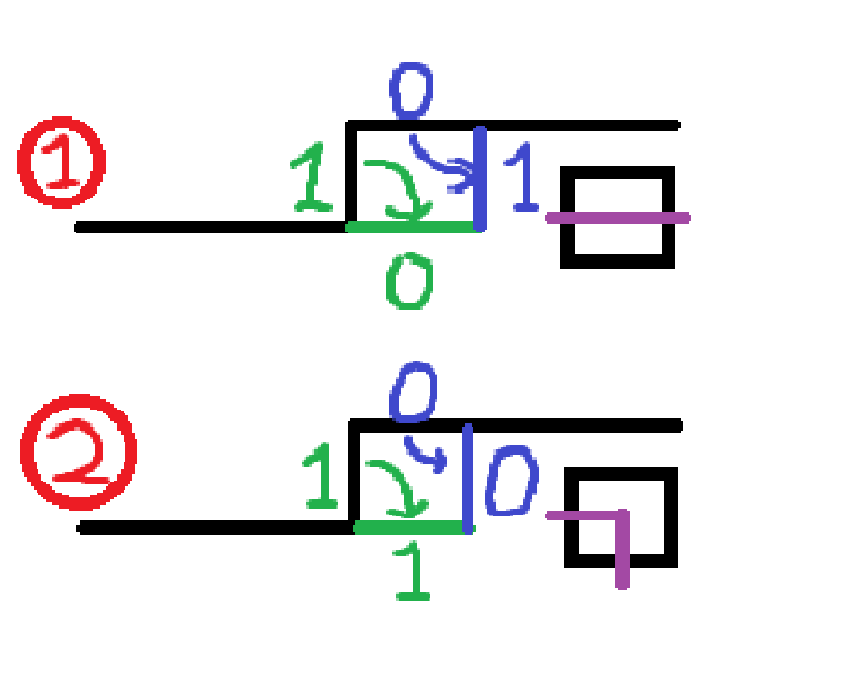
- 上和左均有插头。转移到下无右无。
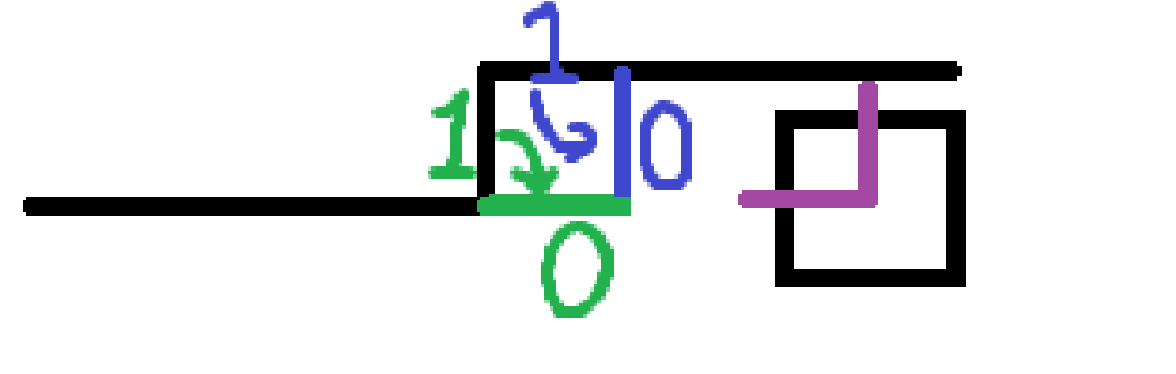
Code(用了滚动数组):
#include<bits/stdc++.h>
#define int long long
// #define double long double
using namespace std;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
int dp1[1<<14],dp2[1<<14];
int n,m;
bool mp[15][15];
void solve()
{
memset(dp1,0,sizeof(dp1));
memset(dp2,0,sizeof(dp2));
n=read();
m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
mp[i][j]=read();
dp2[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
swap(dp1,dp2);
memset(dp2,0,sizeof(dp2));
for(int s=0;s<(1<<(m+1));s++)
{
bool up=s&(1<<(j-1));
bool left=s&(1<<(j));
if(!dp1[s]) continue;
if(mp[i][j]==0)
{
if(left==0&&up==0) dp2[s]+=dp1[s];
continue;
}
if(left==up)
{
dp2[s^(1<<(j-1))^(1<<j)]+=dp1[s];
}
else
{
dp2[s^(1<<(j-1))^(1<<j)]+=dp1[s];
dp2[s]+=dp1[s];
}
}
}
memset(dp1,0,sizeof(dp1));
swap(dp1,dp2);
for(int s=0;s<(1<<m);s++)
dp2[s<<1]=dp1[s];
}
// cout<<n<<" "<<m<<"\n";
cout<<dp2[0]<<"\n";
}
signed main()
{
int T=read();
while(T--) solve();
//mt19937_64 myrand(time(0));
return 0;
}
例题:P5056 【模板】插头 DP
题面:给出 \(n\times m\) 的方格,有些格子不能铺线,其它格子必须铺,形成一个闭合回路。问有多少种铺法?
用 OI-wiki 上的最小表示法。
注意 112200 和 221100 和 113300 和 332200 为同一种情况,这里都编码为 112200。
否则在 \(12 \times 12\) 无障碍的图中跑到第 \(6\) 行就会有 \(9 \times 10^6\) 个状态,会 T 飞。
下面的代码只能用 unordered_map 通过。
最后可以输出 \(ans\),也可以输出 \(dp2[0]\)。
(先咕着)
Code:
#include<bits/stdc++.h>
// #include<bits/extc++.h>
#define int long long
// using namespace __gnu_pbds;
using namespace std;
int n,m;
char mp[15][15];
int ex,ey;
long long ans;
vector<long long> s1,s2;
unordered_map<long long,long long> dp1,dp2;
unordered_map<long long,bool> vis;
const short bits[20]={0,3,6,9,12,15,18,21,24,27,30,33,36,39,42,45};
// void print(int s)
// {
// int num[16]={},max_num=0;
// for(int x=0;x<=m;x++)
// num[x]=((s>>bits[x])&7),max_num=max(max_num,num[x]);
// // cout<<"i="<<i<<" j="<<j<<" s="<<s<<" num:{ ";
// cout<<"print: to_s={ ";
// for(int x=0;x<=m;x++)
// {
// cout<<num[x]<<" ";
// }
// cout<<"} \n";
// }
signed main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>mp[i][j];
if(mp[i][j]=='.') ex=i,ey=j;
}
// for(int i=1;i<=m;i++)
// bits[i]=bits[i-1]+3;
dp2[0]=1;
s2.push_back(0);
for(int i=1;i<=n;i++/*,cout<<"\n"*/)
{
for(int j=1;j<=m;j++/*,cout<<"\n"*/)
{
// cout<<i<<" "<<j<<" "<<s1.size()<<"\n";
dp1.clear();
s1.clear();
vis.clear();
swap(dp1,dp2);
swap(s1,s2);
for(int k=0;k<s1.size();k++/*,cout<<"\n"*/)
{
long long s=s1[k],to_s=0,to_s2=0;
int num[16]={},max_num=0;
for(int x=0;x<=m;x++)
num[x]=((s>>bits[x])&7),max_num=max(max_num,num[x]);
int left=num[j-1];
int up=num[j];
if(mp[i][j]=='*')
{
if(up==0&&left==0)
{
dp2[s]+=dp1[s];
if(!vis[s]) { vis[s]=1; s2.push_back(s); }
// print(s);
}
continue;
}
if(left==0&&up==0)
{
// num[j-1]=num[j]=max_num+1;
// for(int x=m;x>=0;x--)
// to_s=(to_s<<3)|num[x];
// to_s=s|((max_num+1)<<bits[j-1])|((max_num+1)<<bits[j]);
int nwww[15]={};
int tot=0;
num[j]=num[j-1]=10;
nwww[up]=nwww[left]=-1;
for(int x=m;x>=0;x--)
{
to_s<<=3;
if(num[x])
{
if(nwww[num[x]]==0) nwww[num[x]]=++tot;
// else if(nwww[num[x]]==-1) nwww[up]=nwww[left]=++tot;
to_s|=nwww[num[x]];
}
}
dp2[to_s]+=dp1[s];
if(!vis[to_s]) { vis[to_s]=1; s2.push_back(to_s); }
// print(to_s);
}
if((left==0&&up>0)||(left>0&&up==0))
{
to_s2=s;
dp2[to_s2]+=dp1[s];
// swap(num[j-1],num[j]);
// for(int x=m;x>=0;x--)
// to_s=(to_s<<3)|num[x];
// to_s=(s-()-)
to_s=s^(left<<bits[j-1])^(up<<bits[j])^(left<<bits[j])^(up<<bits[j-1]);
dp2[to_s]+=dp1[s];
if(!vis[to_s]) { vis[to_s]=1; s2.push_back(to_s); }
if(!vis[to_s2]) { vis[to_s2]=1; s2.push_back(to_s2); }
// print(to_s);
// print(to_s2);
}
// if(left>0&&up==0)
// if(left==1&&up>1)
// {
// }
// if(left>1&&up==1)
// {
// }
if(left>0&&up>0)
{
if(left==1&&up==1&&i==ex&&j==ey&&max_num==1) ans+=dp1[s];
if(left==up) continue;
int nwww[15]={};
int tot=0;
num[j]=num[j-1]=0;
nwww[up]=nwww[left]=-1;
for(int x=m;x>=0;x--)
{
to_s<<=3;
if(num[x])
{
if(nwww[num[x]]==0) nwww[num[x]]=++tot;
else if(nwww[num[x]]==-1) nwww[up]=nwww[left]=++tot;
to_s|=nwww[num[x]];
}
}
dp2[to_s]+=dp1[s];
if(!vis[to_s]) { vis[to_s]=1; s2.push_back(to_s); }
}
}
}
vis.clear();
s1.clear();
swap(s1,s2);
dp1.clear();
swap(dp1,dp2);
// cout<<" Change Lines: \n";
for(int j=0;j<s1.size();j++)
{
long long s=s1[j];
if(((s>>bits[m])&7)==0)
{
dp2[s<<3]+=dp1[s];
// cout<<" from_s= ";
// print(s);
// cout<<" can_s= ";
// print(s<<3);
// cout<<" \n";
if(!vis[s<<3] )s2.push_back(s<<3);
}
}
}
cout<<ans;
//mt19937_64 myrand(time(0));
return 0;
}
/*
12 12
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
............
*/
练习 1:P3272 [SCOI2011] 地板
设当前状态为 \(s\)。
考虑将轮廓线压成八进制,即 \(s\) 的二进制下每三位表示一个位置。
强制走一步指拐弯后需要走一步,否则地板就不是 L 型了。
每一个位置由 \(abc_{(2)}\) 组成,a 0/1 表示这个位置 不需要/需要强制走一步,b 0/1 表示这个位置 不需要/需要拐弯,c 0/1 表示这个位置 无/有 插头。
发现状态非常臃肿。考虑压缩。
考虑把一个位置压成四进制数。0 表示无插头,1 表示有插头不需要拐弯不需要强制走一步,2 表示有插头需要拐弯,3 表示有插头不需要拐弯不需要强制走一步。
后记:在下文的代码实现中,我们可以进一步压缩状态。0 表示无插头,1 表示有插头不需要拐弯,2 表示有插头需要拐弯。这样只需三进制即可。
四进制压缩《轻微卡常》。
优化策略:
- 使用
bitset<(1<<22)>vis;记录这个状态是否在 s2 中,而不使用bool vis[(1<<22)];。bitset 还是强大。 - 清空时遍历 s1 清空 dp 数组,遍历 dp2 清空 vis 数组来代替 memset。
- 删
#define int long long。 - 使用数组
int dp1[1<<22],dp2[1<<22];代替unordered_map<int,int> dp1,dp2减小常数,
Code:
#include<bits/stdc++.h>
//#include <ext/pb_ds/hash_policy.hpp>
//using namespace __gnu_pbds;
using namespace std;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
inline void write(int x)
{
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int bits[20]={0,2,4,6,8,10,12,14,16,18,20,22,24,26,28,30};
int r,c;
char mp[105][105];
vector<int> s1,s2;
int dp1[1<<22],dp2[1<<22];
//bool vis[1<<22];
bitset<(1<<22)> vis;
//map<int,int> dp1,dp2;
//map<int,bool> vis;
void print(int s);
const int mod=20110520;
void solve(int j,char c,int s,int dp1)
{
int up=(s>>bits[j])&3;
int left=(s>>bits[j-1])&3;
// cout<<"s_before=";
// print(s);
s^=(up<<bits[j])^(left<<bits[j-1]);
if(c=='*')
{
if(up==0&&left==0)
{
dp2[s]+=dp1;
dp2[s]%=mod;
// cout<<"*** up="<<up<<" left="<<left<<" print: "; print(s);
if(!vis[s]) vis[s]=1,s2.push_back(s);
}
return;
}
if(up==3)
{
if(left==3) return;
if(left==2) return;
if(left==1) return;
if(left==0)
{
// s^=(1<<bits[j-1]);
// dp2[s]+=dp1;
// if(!vis[s]) vis[s]=1,s2.push_back(s);
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s);
// return;
dp2[s^(1<<bits[j-1])]+=dp1;
dp2[s^(1<<bits[j-1])]%=mod;
dp2[s]+=dp1;
dp2[s]%=mod;
if(!vis[s^(1<<bits[j-1])]) vis[s^(1<<bits[j-1])]=1,s2.push_back(s^(1<<bits[j-1]));
if(!vis[s]) vis[s]=1,s2.push_back(s);
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(2<<bits[j-1]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(3<<bits[j]));
return;
}
}
if(up==2)
{
if(left==3) return;
if(left==2)
{
dp2[s]+=dp1;
if(!vis[s]) vis[s]=1,s2.push_back(s);
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s);
return;
}
if(left==1) return;
if(left==0)
{
dp2[s^(2<<bits[j-1])]+=dp1;
dp2[s^(3<<bits[j])]+=dp1;
dp2[s^(2<<bits[j-1])]%=mod;
dp2[s^(3<<bits[j])]%=mod;
if(!vis[s^(2<<bits[j-1])]) vis[s^(2<<bits[j-1])]=1,s2.push_back(s^(2<<bits[j-1]));
if(!vis[s^(3<<bits[j])]) vis[s^(3<<bits[j])]=1,s2.push_back(s^(3<<bits[j]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(2<<bits[j-1]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(3<<bits[j]));
return;
}
}
if(up==1)
{
if(left==3) return;
if(left==2) return;
if(left==1) return;
if(left==0)
{
dp2[s^(1<<bits[j-1])]+=dp1;
dp2[s]+=dp1;
dp2[s^(1<<bits[j-1])]%=mod;
dp2[s]%=mod;
if(!vis[s^(1<<bits[j-1])]) vis[s^(1<<bits[j-1])]=1,s2.push_back(s^(1<<bits[j-1]));
if(!vis[s]) vis[s]=1,s2.push_back(s);
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(1<<bits[j-1]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s);
return;
}
}
if(up==0)
{
if(left==3)
{
// s^=(1<<bits[j]);
// dp2[s]+=dp1;
// if(!vis[s]) vis[s]=1,s2.push_back(s);
dp2[s^(1<<bits[j])]+=dp1;
dp2[s]+=dp1;
dp2[s^(1<<bits[j])]%=mod;
dp2[s]%=mod;
if(!vis[s^(1<<bits[j])]) vis[s^(1<<bits[j])]=1,s2.push_back(s^(1<<bits[j]));
if(!vis[s]) vis[s]=1,s2.push_back(s);
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s);
return;
}
if(left==2)
{
dp2[s^(2<<bits[j])]+=dp1;
dp2[s^(3<<bits[j-1])]+=dp1;
dp2[s^(2<<bits[j])]%=mod;
dp2[s^(3<<bits[j-1])]%=mod;
if(!vis[s^(2<<bits[j])]) vis[s^(2<<bits[j])]=1,s2.push_back(s^(2<<bits[j]));
if(!vis[s^(3<<bits[j-1])]) vis[s^(3<<bits[j-1])]=1,s2.push_back(s^(3<<bits[j-1]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(2<<bits[j]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(3<<bits[j-1]));
return;
}
if(left==1)
{
dp2[s^(1<<bits[j])]+=dp1;
dp2[s]+=dp1;
dp2[s^(1<<bits[j])]%=mod;
dp2[s]%=mod;
if(!vis[s^(1<<bits[j])]) vis[s^(1<<bits[j])]=1,s2.push_back(s^(1<<bits[j]));
if(!vis[s]) vis[s]=1,s2.push_back(s);
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(1<<bits[j]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s);
return;
}
if(left==0)
{
dp2[s^(2<<bits[j])]+=dp1;
dp2[s^(2<<bits[j-1])]+=dp1;
dp2[s^(3<<bits[j])^(3<<bits[j-1])]+=dp1;
dp2[s^(2<<bits[j])]%=mod;
dp2[s^(2<<bits[j-1])]%=mod;
dp2[s^(3<<bits[j])^(3<<bits[j-1])]%=mod;
if(!vis[s^(2<<bits[j])]) vis[s^(2<<bits[j])]=1,s2.push_back(s^(2<<bits[j]));
if(!vis[s^(2<<bits[j-1])]) vis[s^(2<<bits[j-1])]=1,s2.push_back(s^(2<<bits[j-1]));
if(!vis[s^(3<<bits[j])^(3<<bits[j-1])]) vis[s^(3<<bits[j])^(3<<bits[j-1])]=1,s2.push_back(s^(3<<bits[j])^(3<<bits[j-1]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(2<<bits[j]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(2<<bits[j-1]));
// cout<<"up="<<up<<" left="<<left<<" print: "; print(s^(3<<bits[j])^(3<<bits[j-1]));
//
return;
}
}
// if((up==3&&left>=2)||(left==3&&up>=2)) return;
}
// void print(int s)
// {
// cout<<"s="<<" ";
// for(int i=0;i<=c;i++)
// cout<<((s>>bits[i])&3)<<" ";
// cout<<"\n";
// }
signed main()
{
// freopen("a.in","r",stdin);
// freopen("out.cpp","w",stdout);
cin>>r>>c;
bool f=0;
if(c>r) f=1;
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)
{
if(f) cin>>mp[j][i];
else cin>>mp[i][j];
}
if(f) swap(r,c);
dp2[0]=1;
s2.push_back(0);
for(int i=1;i<=r;i++)
{
for(int j=1;j<=c;j++)
{
// memset(dp1,0,sizeof(dp1));
// memset(vis,0,sizeof(vis));
// cout<<"i="<<i<<" j="<<j<<"\n";
for(int k=0;k<s1.size();k++) dp1[s1[k]]=0;//,vis[s1[k]]=0;
s1.clear();
// dp1.clear();
// vis.clear();
swap(s1,s2);
swap(dp1,dp2);
for(int k=0;k<s1.size();k++) vis[s1[k]]=0;
// cout<<"i="<<i<<" j="<<j<<" s1.size="<<s1.size()<<"\n";
for(int k=0;k<s1.size();k++) /*cout<<" \ni="<<i<<" j="<<j<<" s="<<s1[k]<<" dp="<<dp1[s1[k]]<<"\n",*/solve(j,mp[i][j],s1[k],dp1[s1[k]]);
// cout<<"\n";
}
// memset(dp1,0,sizeof(dp1));
// memset(vis,0,sizeof(vis));
for(int k=0;k<s1.size();k++) dp1[s1[k]]=0;//,vis[s1[k]]=0;
s1.clear();
// vis.clear();
// dp1.clear();
swap(dp1,dp2);
swap(s1,s2);
for(int k=0;k<s1.size();k++) vis[s1[k]]=0;
for(int j=0;j<s1.size();j++)
{
int s=s1[j];
if(!(s>>bits[c]))
{
dp2[s<<2]+=dp1[s];
dp2[s<<2]%=mod;
if(!vis[s<<2]) vis[s<<2]=1,s2.push_back(s<<2);
// cout<<"dp="<<dp2[s<<2]<<" ";
//
// print(s<<2);
}
}
// cout<<"\n\n\n\n\n";
}
cout<<dp2[0];
return 0;
}
以下是博客签名,正文无关
本文来自博客园,作者:Wy_x,转载请在文首注明原文链接:https://www.cnblogs.com/Wy-x/p/18948894
版权声明:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC-BY-NC-SA 4.0 协议)进行许可。

 解释插头Dp 如何转移以及例题
解释插头Dp 如何转移以及例题

 浙公网安备 33010602011771号
浙公网安备 33010602011771号