前言：这是我 2023 年发现的，当时我比较蒻，只想到了递归实现的，没想到递推实现的。这篇是改成递推之后的。

由于原博客发布时间过早，故重发一遍。

众所周知，分层图最短路用邻接表存常数极大（我只会用邻接表 o(╥﹏╥)o ）。

我们充分发扬人类智慧（其实是当时的我太蒻了，不会建分层图），于是乎，就有了分层图最短路的递推实现方式。

吐槽：某道蓝题（降绿了）Dij 写成 Spfa，吸氧过了。

前置知识：

基础递归。
基础最短路（Dij）模板。
邻接表存图。
STL 中的优先队列 priority_queue，动态数组 vector。

问题引入：P8724 [蓝桥杯 2020 省 AB3] 限高杆

题解

简要题意：
给出 \(n\) 个点和 \(m\) 条边，有的边是断开的，求从断开的边中连上两条边后，点 \(A\) 到点 \(B\) 距离的最小值。

解法一：分层图最短路

显然，我们可以用分层图最短路来实现。建图时，如果这条道路没有限高杆，就在就在每一层中相连；有限高杆就在相邻两层连边。再用 Dij 求最短路。

解法二：

这里提供一个新的解法，基于单层图 Dij 和递推实现（类似延时更改）。

容易发现，连 \(x\) 条边的最短路可由连 \(x-1\) 条边的最短路拓展而来，即转移而来。

因为连上一条边后，新图的最短路一定不长于原图最短路。

关于后效性，每个点的最短路径相对独立，而且不会连重边（因为连重边之后肯定不优于不连重边，如果真连到重边，那么在下文 copy_queue 时情况会被舍弃），所以无后效性。

故本算法正确。复杂度蒟蒻不会证。反正能过。跑得还很快。

设起点为 \(1\)，终点为 \(10\)，每条红边需要 \(k\) 的代价才可连上，而且连边次数有限制，不能连超过 \(cnt\) 条红边。

本题中 \(k=0,cnt=2\)。

注：图中红边边权均为 \(0\)。

起初，所有红边是断开的，最短路由一次 Dij 即可得出。

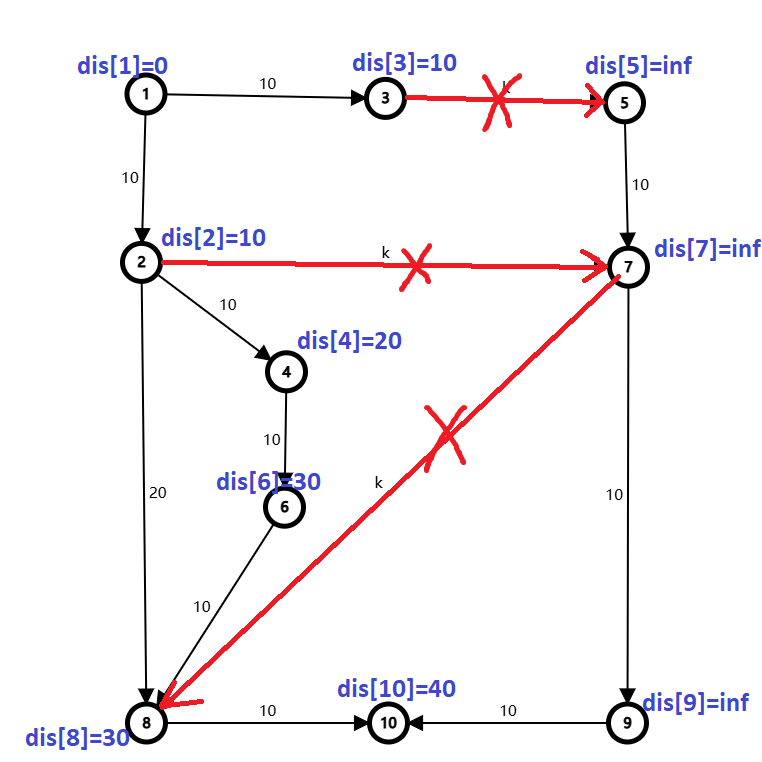
现在我们要选一条红边连上。

显然的想法是，枚举每条红边起点，尝试连上这条红边，同时更新最短路。

若连红边 \(3 \to 5\)，最短路被更新成：

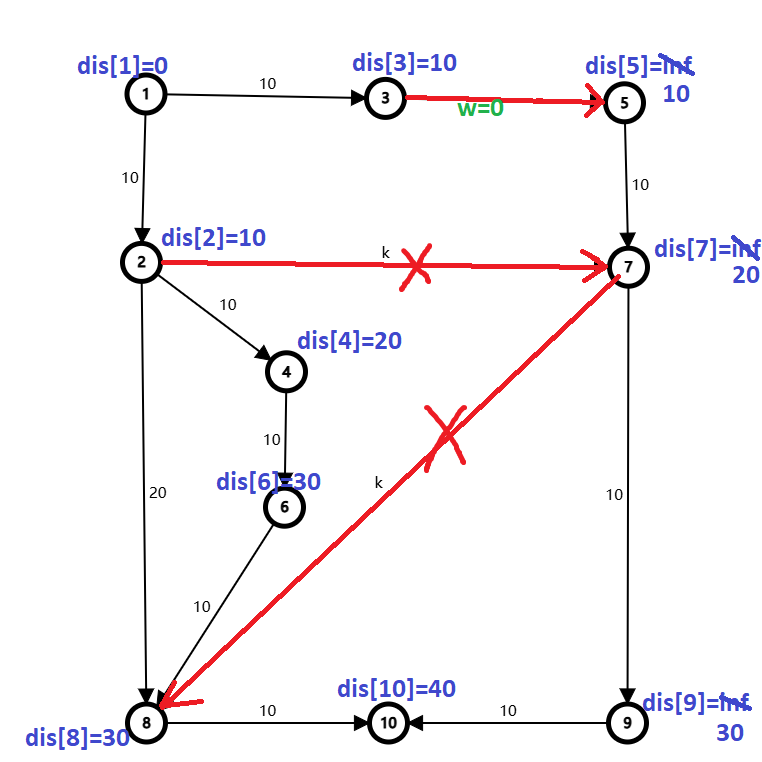
如果能连上 \(cnt\) 条边，则执行 \(cnt\) 次 Dij。

每次 Dij 基本操作如下：

若该次遍历到的边（即原图上原有的边）没有被断开，执行普通 Dij。

if(dis[k]>dis[x]+w)//普通 Dij 松弛操作
{
    dis[k]=dis[x]+w;
    q.push(make_pair(dis[k],k));
}

若边断开（要连边），将现在的最短路径加上该边边权，将该值和这条边通向的点扔入另一个记录用的 priority_queue（也可以用别的记录方式存，不影响最终结果）。

if(d) q2.push(make_pair(min(dis[k],dis[x]+w),k));
//注意把长度取min，否则拆除后最短路无法保证

当此次 Dij 结束时，将记录用 priority_queue 中元素（q2 中的）复制到执行 Dij 所用 priority_queue 里（q1 里），并清空 q2。

//朴素剪切代码
void copy_queue()
{
	while(!q.empty()) q.pop();
	while(!q2.empty()) q.push(q2.top()),dis[q2.top().second]=min(dis[q2.top().second],q2.top().first),q2.pop();
	//同时更新dis记录的最短路（类似延时更改）
}

此题中要我们求连上断开边中的两条边后，A 到 B 的最短路，容易得出以下代码（用循环 \(cnt\) 次实现，优化常数）：


for(int cnt=0;cnt<=2;cnt++) dij();//现在拆了 cnt 个限高杆，没拆够两个限高杆，继续拆。

本题 AC 代码：

#include<bits/stdc++.h>
#define reg register
#define int long long
using namespace std; 
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q,q2;

int n,m;
vector<int> E[100005],V[100005];
vector<int> D[100005];
int maxn=-999999999,minn=9999999999;
int dis[1<<20];
bool vis[1<<20];

void copy_queue()
{
	while(!q.empty()) q.pop();
	while(!q2.empty()) q.push(q2.top()),dis[q2.top().second]=min(dis[q2.top().second],q2.top().first),q2.pop();
	//同时更新dis记录的最短路（类似延时更改）
}

void add(int a,int b,int c,int d)
{//加点操作
	E[a].push_back(b);
	V[a].push_back(c);
	D[a].push_back(d);
}

void dij()
{
	memset(vis,0,sizeof(vis));
	//清空vis数组
	copy_queue();//把 q_2 附给 q
	
	while(q.size())
	{
		int x=q.top().second;
		q.pop();
		
		if(vis[x]) continue;//到过这个节点
		vis[x]=1;//记录
		
		for(int i=0;i<E[x].size();i++)
		{
			int k=E[x][i];
			int w=V[x][i];
			int d=D[x][i];
            if(dis[k]<=dis[x]+w) continue;
			
			if(d) q2.push(make_pair(min(dis[k],dis[x]+w),k));
			//注意把长度取min，否则拆除后最短路无法保证
			else//松弛操作
			{
				dis[k]=dis[x]+w;
				q.push(make_pair(dis[k],k));
			}
		}
	}
	maxn=max(maxn,dis[n]);//这里是记录没拆限高杆时的最短路
	minn=min(minn,dis[n]);//拆限高杆后的最短路
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	//加速
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int a,b,c,d;
		cin>>a>>b>>c>>d;
		add(a,b,c,d);
		add(b,a,c,d);
	}
	
	memset(dis,0x3f,sizeof(dis));
	//初始化dis为无穷大
	dis[1]=0;
	q2.push(make_pair(dis[1],1));
	//往q_2中加入起点，
	//经过copy_queue()后就在 q 中了
    for(int i=0;i<=2;i++) dij();//枚举拆到多少条边
	
	cout<<maxn-minn;
	return 0;
}

~~好了，没了。完结撒花！~~

例题 1：P4568 [JLOI2011] 飞行路线

~~对，你没有看错，就是 Spfa 能过的那个。~~

读题可以发现，题目给出双向边，要求我们建 \(k\) 层图。

用递推实现，递推 \(k\) 次，就是 for(int cnt=0;cnt<=k;cnt++) dij();

优化：若 Dij 到连 \(cnt\) 条边时，不存在一个点的最短路被更新，就可以退出循环了。因为再多连边，肯定不劣于连 \(cnt\) 条边的情况，而连 \(cnt\) 条边已经是最优了，所以不用考虑再连边的情况。

本题与上题几乎没有区别，所以就不写注释了。~~才不是因为我懒。~~

AC 代码：


#include<bits/stdc++.h>
using namespace std; 

int n,m,k;
int s,t;
vector<int> E[10005],V[10005];
bool vis[10005];
int dis[10005];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
queue<pair<int,int> > q2;

int minn=9999999999;
void add(int x,int y,int z)
{
	E[x].push_back(y);
	V[x].push_back(z);
}

void copy_queue()
{
	while(!q.empty()) q.pop();
	while(!q2.empty())
	{
		int k=q2.front().second;
		int w=q2.front().first;
		
		if(dis[k]>=w) q.push(q2.front());
		dis[k]=min(dis[k],w);
		q2.pop();
	}
}

void dij()
{
	memset(vis,0,sizeof(vis));
	copy_queue();
	while(q.size())
	{
		int x=q.top().second;
		q.pop();
		
		if(vis[x]) continue;
		vis[x]=1;
		
		for(int i=0;i<E[x].size();i++)
		{
			int k=E[x][i];
			int w=V[x][i];
			
			if(dis[x]<dis[k]) q2.push(make_pair(dis[x],k));
			if(dis[k]>dis[x]+w)
			{
				dis[k]=dis[x]+w;
				q.push(make_pair(dis[k],k));
			}
		}
	}
	
	minn=min(minn,dis[t]);
}

signed main()
{
	memset(dis,0x3f,sizeof(dis));
	
	cin>>n>>m>>k;
	cin>>s>>t;
	
	for(int i=1;i<=m;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		add(x,y,z);
		add(y,x,z);
	}
	
	dis[s]=0;
	q2.push(make_pair(dis[s],s));
    for(int i=0;i<=k;i++) dij();
	cout<<minn;
	return 0;
}

练习：

P1948 [USACO08JAN] Telephone Lines S

P2939 [USACO09FEB] Revamping Trails G

P4822 [BJWC2012] 冻结

优缺点分析：

优点：编码容易，易于理解。

缺点：复杂度未知。但是没有被卡过。

PS：这个做法应该可过 NOI2025 Day1T1。

posted @ 2025-07-07 19:48 Wy_x 阅读(47) 评论(0) 收藏举报

刷新页面返回顶部

༼ つ ◕_◕ ༽つ Wy-x 的 blog 🤗

凤凰台上凤凰游，凤去台空江自流。

关于分层图最短路的递推实现方式