任务安排 4.1 题解

1. 暴力Dp（任务安排 1）

采用费用提前计算。

定义 \(t[i]\) 为 \(t\) 的前缀和，\(f[i]\) 为 \(c\) 的前缀和。

转移方程为：

\[dp[i]=min(dp[j]+(f[i]-f[j])*t[i]+s*(f[n]-f[i])) \]

\[(0 \le j < i) \]

初始化 $$dp[0]=s*f[n]$$

2. 斜率优化（任务安排 2）

把 \(\min\) 去掉，拆项，移项，将 Dp 方程化为 \(y=kx+b\) 的形式，其中，\(x,\ y\) 仅与 \(j\) 有关，\(k,\ b\) 仅与 \(i\) 有关。

\[dp[j]=t[i]*f[j]+(dp[i]-f[i]*t[i]-s*f[n]+s*f[i]) \]

\[(0 \le j < i) \]

初始化$$dp[0]=s*f[n]$$

其中，

\[x=f[j] \]

\[y=dp[j] \]

\[k=t[i] \]

\[b=dp[i]-f[i]*t[i]-s*f[n]+s*f[i] \]

（下文中 \(x,y,k,b\) 均与上式意义相同）

使 \(dp[i]\) 最小，就要让 \(k=t[i]\) 这条直线去截点 \((x,y)\)，截距最小，则解出的 \(dp[i]\) 最小。

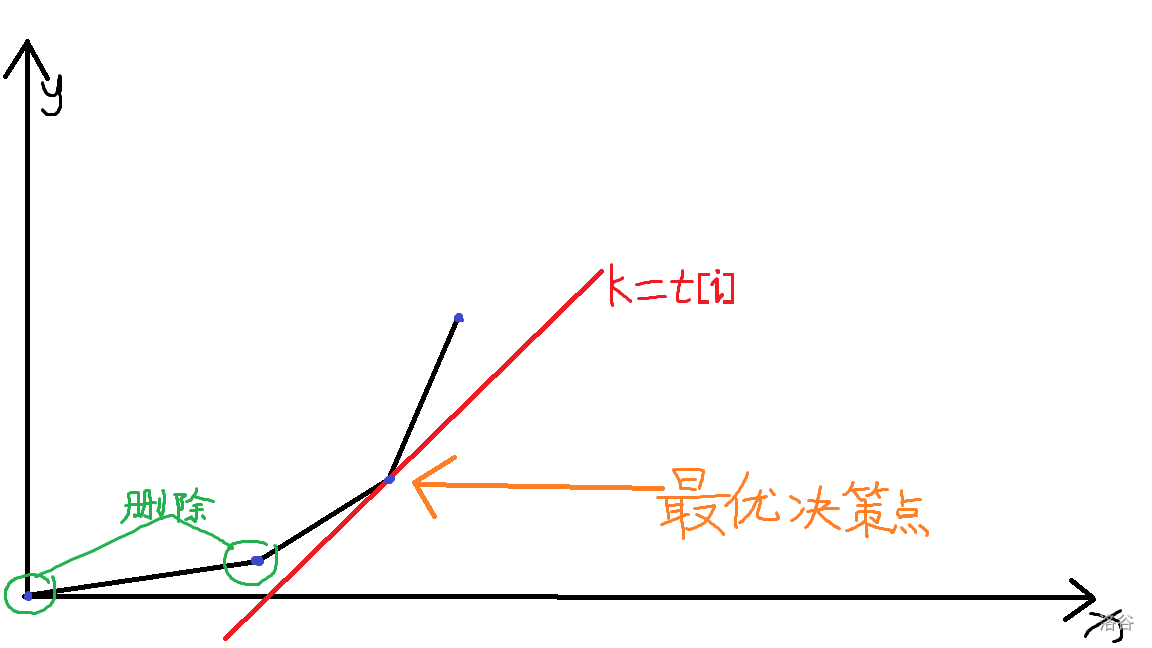
所以我们维护下凸包。

Update：当然你用李超树就可以简单实现。

3. vector 代替平衡树（任务安排 4.1）

前置知识：

v.insert(v.begin()+i,x);
//在 v 的第 i+1 个元素前面（从第 1 个算起），插入数值x，如 v 为1,2,3,4，i=1,插入元素后为1,5,2,3,4。
//即为在 v 中下标为 i 的元素前面（下标从 0 开始）插入数值x，

v.erase(v.begin()+i);//删除 v 中下标为 i 的元素（下标从 0 开始）

在任务安排 4 中，\(x\) 不单调，这就意味着如果我们按原方程 Dp，需要动态插点，因为斜率优化的前提（候选集合）是 \(x\) 单调的。

蓝书有言：可以倒序 Dp，让仍具有单调性的 \(k\) 作为 \(x'\)，跑 Dp。

我们发现，动态插点平衡树可以实现，平衡树又可以用 vector 实现，所以我们尝试 vector 暴力维护凸包。

插点时，我们需要在凸包上二分，找到第一个横坐标大于 \(x\) 的点，在这个点前执行插入操作。

插点后，讨论两种情况：

设新插入的点为 \(P\)。

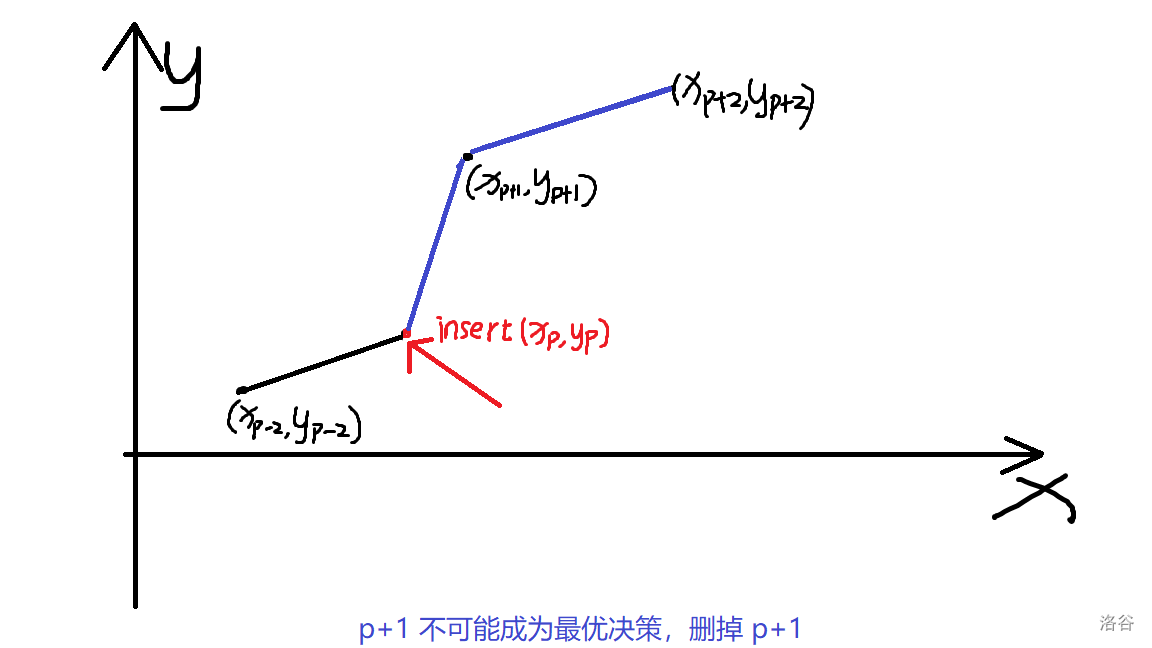
1. 如图，\(P-1,P,P+1\) 三个点构成上凸包，那么 \(P\) 点不可能成为最优决策，删掉 \(P\)。

2. 如图，\(P,P-1,P-2\) 三个点构成上凸包，那么 \(P-1\) 点不可能成为最优决策，删掉 \(P-1\)，直到 \(P\) 左侧只有一个点或 \(P,P-1,P-2\) 三个点构成下凸包。

3. 如图，\(P,P+1,P+2\) 三个点构成上凸包，那么 \(P+1\) 点不可能成为最优决策，删掉 \(P+1\)，直到 \(P\) 右侧只有一个点或 \(P,P+1,P+2\) 三个点构成下凸包。

Code：

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar()                                                              \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt)     \
	? EOF                                                                 \
	: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
	int x=0,c=getchar(),f=0;
	for(;c>'9'||c<'0';f=c=='-',c=getchar());
	for(;c>='0'&&c<='9';c=getchar())
		x=(x<<1)+(x<<3)+(c^48);
	return f?-x:x;
}
inline void write(int x)
{
	if(x<0) x=-x,putchar('-');
	if(x>9)  write(x/10);
	putchar(x%10+'0');
}

int n,s;
int t[1<<20],f[1<<20];
int dp[1<<20];

struct Node{
    int x,y,id;
};
vector<Node> v;

#define X(i) (f[i])
#define Y(i) (dp[i])
#define K(i) (t[i])

int find(const Node x)
{
    int l=0,r=v.size()-1;
    while(l<r)
    {
        int mid=(l+r)>>1;
        if(v[mid].x<x.x) l=mid+1;
        else r=mid-1;
    }
    l-=5;
    r+=5;
    if(l<0) l=0;
    if(r>=v.size()) r=v.size()-1;
    for(int i=r;i>=l;i--)
    if(v[i].x<=x.x) return i+1;
    return 0;
}

signed main()
{
    n=read();
    s=read();
    for(int i=1;i<=n;i++)
    {
        int ti=read(),fi=read();
        t[i]=t[i-1]+ti;
        f[i]=f[i-1]+fi;
    }
    memset(dp,0x3f,sizeof(dp));
    dp[0]=s*f[n];
    v.push_back({X(0),Y(0),0});
    for(int i=1;i<=n;i++)
    {
        while(v.size()>1&&(v[1].y-v[0].y)<=K(i)*(v[1].x-v[0].x)) v.erase(v.begin());
        int p=v[0].id;
        dp[i]=dp[p]+(f[i]-f[p])*t[i]+s*(f[n]-f[i]);
        dp[i]=min(dp[i],dp[0]+(f[i]-f[0])*t[i]+s*(f[n]-f[i]));

        Node nw={X(i),Y(i),i};
        p=find(nw);//vector 中二分出第一个 x >= X(i) 的点在 vector 中下标
        v.insert(v.begin()+p,nw);//先插入
        if(p>0&&p<v.size()-1)//第 1 种情况
        {
            if((v[p+1].y-v[p].y)*(v[p].x-v[p-1].x)<=(v[p].y-v[p-1].y)*(v[p+1].x-v[p].x))
            {
                v.erase(v.begin()+p);
                continue;
            }
        }
        while(p>1&&(v[p].y-v[p-1].y)*(v[p-1].x-v[p-2].x)<=(v[p-1].y-v[p-2].y)*(v[p].x-v[p-1].x))
        {//第 2 种情况
            v.erase(v.begin()+p-1);
            p--;
        }
        while(p<v.size()-2&&(v[p+2].y-v[p+1].y)*(v[p+1].x-v[p].x)<=(v[p+1].y-v[p].y)*(v[p+2].x-v[p+1].x))
        {//第 3 种情况
            v.erase(v.begin()+p+1);
            // p++;
        }
        
        // while()
        // for(int j=0;j<i;j++)
        // dp[i]=min(dp[i],dp[j]+(f[i]-f[j])*t[i]+s*(f[n]-f[i]));
    }
    cout<<dp[n];
	return 0;
}