P9232 [蓝桥杯 2023 省 A] 更小的数 题解

题目传送门

题意：

给定一个字符串，在其中选出一段连续的子串并将子串进行反转，最多反转一次，反转后再放入原位置处得到的新的数字，如果新的数字比原来的数字小则算做一种方案。

求一共有多少种不同的子串选择方案。

• 注意：允许有前导零的存在。

解法：

数据范围：\(1 \le n \le 5000\)，时间复杂度 \(O(n^2)\) 即可通过。

看图：

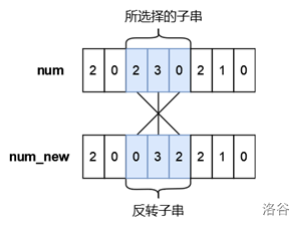
易知：如果在一个区间中，反转子串小于所选择的子串，那么这种方案可行。反之，则不行。

代码：

#include<bits/stdc++.h>

using namespace std; 

signed main()
{
	string a;
	cin>>a;//给定数字用字符串记录 
	int l=a.size(),ans=0;
	//ans 记录答案 
	
	for(int i=0;i<l-1;i++)//枚举区间左端点 0~l-1 
	{
		for(int j=i+1;j<l;j++)
		//在左端点以右枚举区间右端点 i+1~l-1 
		{
			int ii=i,jj=j;
			
			while(ii<=j)
			{
				if(a[jj]<a[ii]) ans++;
				if(a[jj]!=a[ii]) break;
				//如果 a[jj]<a[ii]，此方案成立，计数器加一的同时结束此循环 
				//如果 a[jj]>a[ii]，反转数字大于给定数字，结束此循环
				//简化，当 a[jj]!=a[ii] 时，结束循环 
				ii++;jj--;
				//左指针右移，右指针左移 
			}
		}
	} 
	
	cout<<ans;
	return 0;
}