网络流训练专题
\(\text{Part 1.最大流}\)
概述(From OI Wiki)
网络(network)是指一个特殊的有向图 \(G=(V,E)\),其与一般有向图的不同之处在于有容量和源汇点。
-
\(E\) 中的每条边 \((u, v)\) 都有一个被称为容量(capacity)的权值,记作 \(c(u, v)\)。当 \((u,v)\notin E\) 时,可以假定 \(c(u,v)=0\)。
-
\(V\) 中有两个特殊的点:源点(source)\(s\) 和汇点(sink)\(t\)(\(s \neq t\))。
对于网络 \(G=(V, E)\),流(flow)是一个从边集 \(E\) 到整数集或实数集的函数,其满足以下性质。
- 容量限制:对于每条边,流经该边的流量不得超过该边的容量,即 \(0 \leq f(u,v) \leq c(u,v)\);
- 流守恒性:除源汇点外,任意结点 \(u\) 的净流量为 \(0\)。其中,我们定义 \(u\) 的净流量为 \(f(u) = \sum_{x \in V} f(u, x) - \sum_{x \in V} f(x, u)\)。
对于网络 \(G = (V, E)\) 和其上的流 \(f\),我们定义 \(f\) 的流量 \(|f|\) 为 \(s\) 的净流量 \(f(s)\)。作为流守恒性的推论,这也等于 \(t\) 的净流量的相反数 \(-f(t)\)。
对于网络 \(G = (V, E)\),如果 \(\{S, T\}\) 是 \(V\) 的划分(即 \(S \cup T = V\) 且 \(S \cap T = \varnothing\)),且满足 \(s \in S, t \in T\),则我们称 \(\{S, T\}\) 是 \(G\) 的一个 \(s\)-\(t\) 割(cut)。我们定义 \(s\)-\(t\) 割 \(\{S, T\}\) 的容量为 \(||S, T|| = \sum_{u \in S} \sum_{v \in T} c(u, v)\)。
人话(不严谨):
最大流:给出一个有容量和源点、汇点的有向图。把每条边看成一条水管,那么最大流就是把水从自来水厂送到你家的水量最大值,其中水管不能爆掉,且除了源汇点的其他点流入量必须等于流出量。
最小割:给出一个边带权无向图,问从 \(S\) 不能到达 \(T\) 所需要删去边的最小边权之和。
[USACO4.2] 草地排水Drainage Ditches
省流:模板题省毛流
思路
模板题,直接建图跑最大流。
CF546E Soldier and Traveling
省流:给出一个无向图,第 \(i\) 个点上有 \(a_i\) 个士兵。每个士兵可以移动到跟自己相邻的点上,问是否可以使一些士兵移动后使得第 \(i\) 个点上有 \(b_i\) 个士兵,并给出方案。
思路
根据数据范围和标签我们可以大致猜到这是一道网络流题目。考虑该怎么建图。
我们可以建立二分图,其中左边部分的点表示原来的士兵,右边部分的点表示移动后的士兵,再建立超级源点和汇点 \(S,T\)。
显然原来 \(i\) 点士兵有 \(a_i\) 个,可以贡献 \(a_i\) 的流量;移动后 \(i\) 点士兵有 \(b_i\) 个,需要接受 \(b_i\) 的流量。于是我们将 \(S\) 与左部的第 \(i\) 个点连边,容量为 \(a_i\),将右边的点 \(i\) 与 \(T\) 连边,容量为 \(b_i\)。
对于每个点的士兵可以停留在原地,也可以移动到相邻的点。于是我们将左部 \(i\) 号点与右部 \(i\) 号点连边,这条边表示不动的士兵。对于原图上的无向边 \((i,j)\),我们将左部的 \(i\) 号点与右部的 \(j\) 号点连边,左部的 \(j\) 号点与右部的 \(i\) 号点连边,表示移动的士兵。因为可以移动任意数量的士兵,所以容量均为无限大。
跑完一遍网络流后,我们判一下 \(S\to i\) 与 \(j\to T\) 的边是否满流,若满流,则表示所有士兵都顺利转移,否则无解。求方案只需要看图上 \(i\to j\) 的每条边减少的流量即可。
POJ1149/SP4063 卖猪问题
省流:有一堆猪圈,每个猪圈有一堆猪,每次有人来买指定数量的猪,他可以买他指定的猪圈中的猪并调整这些猪圈中猪的数量,问最多可以卖多少猪。
思路
网络流好题。
发现人的要求和猪圈中猪的数量直接处理不好建图,于是考虑对每个人和每个猪圈拆点建图。
具体来说,将每个人拆成两个点,容量为他要购买的猪的数量,将每个猪圈拆成两个点,容量为猪圈中猪的数量。
由于有多个顾客和猪圈,所以考虑建立超级源点与汇点,流向便为源点流向每个人,每个人流向猪圈,猪圈流向汇点。
建边时将源点与每个人的起始点连边,将每个人的结束点与他有钥匙的猪圈的起始点连边,将猪圈的结束点与汇点连边,容量均为无限大,跑一遍最大流即可。然后你就会发现样例都没过。
哪里错了?因为每个人还可以调整每个猪圈中猪的数量,所以每个人的结束点不仅要跟猪圈连边,还要跟之前能到达这个猪圈的人连边,这样可以使得这个人的流可以流到之前顾客能解锁的猪圈中的猪,也就保证了之前的顾客能够调整这个猪圈中猪的数量。
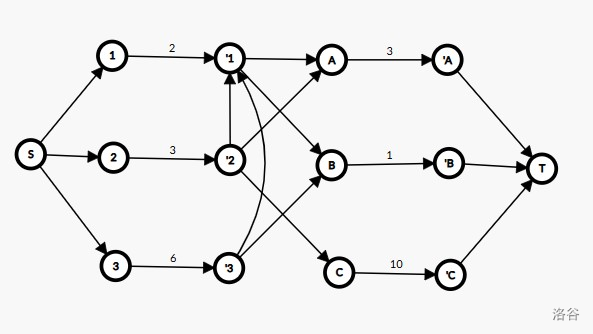
考虑样例:
3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6
建图如下:
[USACO07OPEN] Dining G
省流:每个奶牛有喜欢的食物或饮料,每种食物或饮料只能供一头牛享用,且每头牛只享用一种食物和一种饮料。问最多几头奶牛可以同时满足食物和饮料的要求。
思路
可以同样拆点,建立超级源汇点,点之间容量为 \(1\)。
发现如果源点先流向奶牛那么需要同时满足两个条件,不好建图。于是可以建图使得源点先流向食物,食物流向奶牛,奶牛流向饮料,饮料流向汇点,这样便满足了奶牛可以同时满足这两个条件。
[SCOI2012] 奇怪的游戏
省流:\(n\times m\) 的数字矩阵,每次操作可以使相邻两个数加 \(1\),问使矩阵变为同一个数的最少操作次数。
思路
相邻加数考虑黑白染色。发现每次加 \(1\) 相当于把黑色格子和白色格子的权值都加 \(1\),所以无论怎么操作黑色格子和白色格子的权值增加量是相等的。
于是我们设最终矩阵得到相等的数为 \(x\),黑格子数量为 \(cnt_b\),白格子数量为 \(cnt_w\),现在的黑色格子权值和为 \(v_b\),白色格子权值和为 \(v_w\),于是我们有:
观察该柿子,发现 \(x\) 仅当 \(cnt_b\neq cnt_w\) 时有解,且仅当 \(nm\) 为奇数时有 \(|cnt_b-cnt_w|=1\)。于是当 \(nm\) 为奇数时,可以直接解出 \(x\),但是此时的正确性还不能保证。当 \(nm\) 为偶数时,观察到若 \(x\) 可以通过操作得到的话,\(x+1\) 也一定可以通过对 \(x\) 的情况整体加 \(1\) 得到;同理若 \(x\) 不能通过操作得到,那么 \(x-1\) 也一定不能得到,即 \(x\) 具有单调性,可以二分。
现在发现不管是 \(nm\) 为奇数时的 \(x\) 的正确性,还是 \(nm\) 为偶数中二分的 \(\text{check}\),都需要建图判定。
我们可以将 \(S\) 与所有黑点连边,容量为权值之差;将白点与 \(T\) 连边,容量同样为权值之差,将黑点与相邻白点连边,容量为无限大,跑网络流判断黑点流量是否等于白点流量即可。
[CQOI2014]危桥通行
省流:无向图,有的边只能走 \(2\) 次。有两个人在 \(a_1\),\(b_1\)。要求从点 \(a_1\) 到点 \(a_2\) 往返 \(a_n\) 次,从点 \(b_1\) 到点 \(b_2\) 往返 \(b_n\) 次,问是否能满足要求。
思路
对所有危桥建边,容量为 \(1\),对所有普通桥建边,容量为 \(INF\)。将超级源点 \(S\) 与 \(a_1\) 和 \(b_1\) 连边,边权为 \(an\) 和 \(bn\),\(a_2\) 和 \(b_2\) 与超级汇点连边,边权为 \(an\) 和 \(bn\),跑一遍最大流检查流量是否是满的(即满足了要求)即可。
然后你打完就发现你WA了(
注意到流量满时可能 \(b_2\) 的一部分流量来自 \(a_1\),\(a_2\) 同理也可能来自 \(b_1\)。处理很简单,只需要将 \(b_1\) 和 \(b_2\) 交换再跑一遍最大流即可。
[SCOI2007]蜥蜴
省流:有一堆有高度的柱子和一堆蜥蜴,蜥蜴可以跳到两点平面距离不超过一定值且没有蜥蜴的柱子上并使原来的柱子高度减 \(1\),当蜥蜴跳出边界时它逃离,问最多多少蜥蜴能逃离。
思路
将每个柱子拆点,容量为柱子的高度,对于每个柱子到蜥蜴能跳到的其他柱子,将该柱子的结束点和另一个柱子的起始点连边,容量无限大,这样就可以保证从一个柱子跳到另一个柱子能使得柱子的流量减 \(1\)。
建立超级源点与汇点。对于每只蜥蜴所在的位置,将源点与该位置的起始点连边,边权为 \(1\)。对于所有能跳出去的柱子,将它与超级汇点连边,边权无限大(因为可能不止一个蜥蜴从这根柱子跳出去)。跑一遍最大流即可得出能逃出去蜥蜴的最大值,拿总蜥蜴数一减就能得到逃不出去的最小值。
[国家集训队] happiness
省流:\(n\times m\) 的矩阵每个格子可以选择 \(a_i\) 或 \(b_i\) 的价值,相邻的格子都选 \(a_i\) 或都选 \(b_i\) 会有不同的额外价值,求最大价值。
思路
因为每个格子只能选择 \(a_i\) 或 \(b_i\),所以考虑建图求出最小割,拿总价值减去最小割即为最大价值。
考虑如下建图方式:
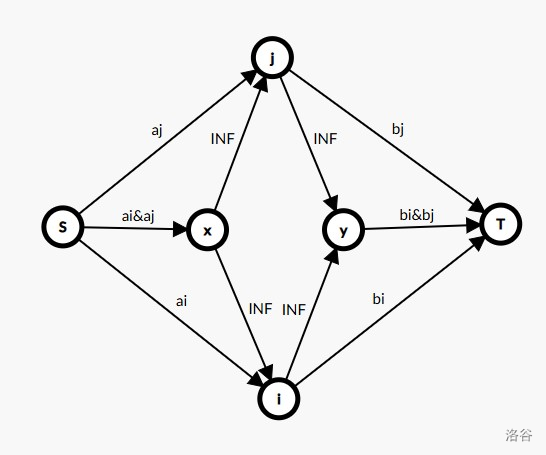
\(S\) 为源点,\(T\) 为汇点,\(i,j\) 为矩阵中的任意相邻两个点,\(a_i,a_j,b_i,b_j\) 表示 \(i,j\) 选 \(a,b\) 的价值,\(a_i\&a_j\) 和 \(b_i\&b_j\) 表示同时选 \(a\) 或 \(b\) 的额外价值,总价值为除 \(INF\) 以外边的总和。
则该图有以下几种可能的割:
-
\(a_i,a_j,a_i\&a_j\) 表示 \(i,j\) 均选 \(b\),则此时的价值为 \(b_i+b_j+b_i\&b_j\)。
-
\(b_i,b_j,b_i\&b_j\) 表示 \(i,j\) 均选 \(a\),则此时的价值为 \(a_i+a_j+a_i\&a_j\)。
-
\(a_i,b_j,a_i\&a_j,b_i\&b_j\) 表示 \(i\) 选 \(b\),\(j\) 选 \(a\),则此时的价值为 \(b_i+a_j\)。
-
\(b_i,a_j,a_i\&a_j,b_i\&b_j\) 表示 \(i\) 选 \(a\),\(j\) 选 \(b\),则此时的价值为 \(a_i+b_j\)。
然后跑一遍最大流求出最小割即可过掉。
文理分科
省流:\(n\times m\) 的矩阵每个格子可以选择 \(a_i\) 或 \(b_i\) 的价值,自己及相邻的格子都选 \(a_i\) 或都选 \(b_i\) 会有不同的额外价值,求最大价值。
思路
一模一样的思路,如法炮制建图即可。
太空飞行计划问题
省流:有 \(n\) 种器材,每种器材要花费 \(c_i\) 元。有 \(m\) 个实验,每个实验需要用这些器材中的一些器材,若器材都有则获得 \(p_i\) 元。问最多能获得多少元。
思路
考虑建立最小割模型。
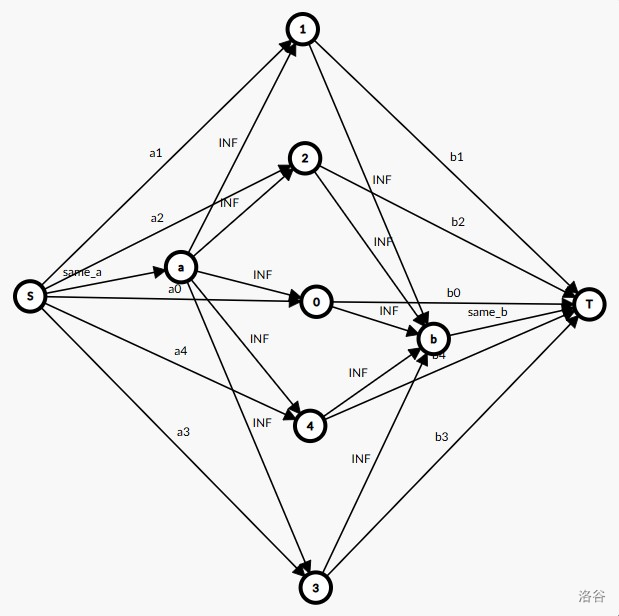
发现我们要让获得的钱尽可能多,让花费的钱尽可能少,于是我们可以用以下方式建图:
建立超级源点 \(S\) 与 \(T\),将 \(S\) 与每种实验连边,容量为 \(p_i\)。将每种实验跟器材连边,容量无限大。将每种器材跟 \(T\) 连边,容量为 \(c_i\),最后拿 \(\sum p_i\) 减去最小割即为答案。
因为求得是最小割,所以割掉的 \(p_i\) 与 \(c_i\) 都是最小的,但是最后又用 \(\sum p_i\) 减掉了,因为为减法,所以最后得到的 \(\sum p_i-p_i\) 是最大的,\(-c_i\) 也是最大的,也就是减去的最少,代价最大。
裁员
省流:求最大权闭合子图及其最小边数。
最大权闭合子图:找到一个点的集合,使得从任意一个点出发,能够到达的点都在该集合中,并且这些点的权值(可能为负)之和最大。
思路
其实上一题就是最大权闭合子图模板题但是我忘说了。
我们首先把原图建出来,容量为无限大。建立超级源汇点 \(S,T\)。将 \(S\) 与所有正权节点连边,容量为权值。将所有负权节点与 \(T\) 连边,容量为权值的相反数,跑一遍最小割,拿正权之和减去最小割即为答案。
证明这样做为什么是对的。设 \(S\) 与正权节点有连边表示选择该点,负权节点与 \(T\) 有连边表示不选该点。
那么当 \(S\) 与 \(T\) 连通(即不存在割时)时,则一个正权节点一定能到达负权节点,选择的节点与不选的节点连通,显然不满足定义。
当一条正权节点的边没被割掉时,显然它后面的所有负权节点都会被割掉,且正权节点不会被割掉,满足定义。
因为求出来的正权节点的权值之和为最小值,所以拿总数减掉后即为最大值,且最小负权之和恰好变为最大负权之和。
对于最少人数,只需遍历一遍残量网络求出可达点个数即可。
CF1082G Petya and Graph
省流:定义图权为图中边权总和−图中点权总和(空图的图权=0),求一个无向图最大权子图。
思路
每个点选或不选,选择一些点有额外收益,考虑最小割。
可以发现,每选择一个点会减少一些代价,选择有连边的点会增加一些代价,转换成每次割掉一条边会增加一些代价,割掉原图上有连边的边可以不用割掉额外代价的边。
于是我们将每个点与 \(T\) 连边,容量为点权。将 \(S\) 与每条边连边,容量为边权,将每条边与它连接的两个点连边,容量为无限大。跑一遍最大流,拿边权总代价减去最小割即可。
[NOI2009] 植物大战僵尸
不省流:在一个网格上每格都有一个植物,植物能攻击到除自己以外的位置的一些位置,当植物被吃掉时获得该植物的得分(可能为负)。你可以派僵尸吃植物,植物只能从后往前吃,且路径上不能有植物能攻击到的地方。问最大得分为多少。
思路
有负分,得到得分有条件,最大权闭合子图秒了。
因为植物只能从后往前吃,所以我们将植物从前往后连边。因为最大权闭合子图的性质,所以吃掉一个植物一定会吃掉它后面的所有植物。对于攻击的位置我们将攻击位置的植物与攻击的植物连边,这样如果要吃攻击位置的植物,就一定要吃掉攻击的植物。
正负权植物连边方式同上,\(S\) 连正权点,负权点连 \(T\)。然后就是喜闻乐见的样例都没过。
观察到直接这样连边可能会出现僵尸创进一个 SCC 中将这个 SCC 中的植物全吃掉,而这个 SCC 中的植物是互相保护的且被 SCC 中植物保护的植物都不可能被吃掉。所以我们求出网络的 SCC,对于大小比 \(1\) 大的 SCC,这里面的植物都是相互保护的,所以将这里面的植物向 \(T\) 连边权为无限大的边,这样就解决了该问题。
[ABC397G] Maximize Distance
省流:给出一个有向图,你需要选择 \(k\) 条边让它们的边权为 \(1\),剩余边的边权为 \(0\)。问 \(1\) 到 \(n\) 的最短路长度的最大值为多少。
思路
最短路最大值显然二分答案,考虑给出最短路的长度如何计算最少需要的边数。
若最短路长度等于 \(1\),则问题就变为了选择最少的边使得从 \(1\) 到 \(n\) 的每条路径都经过至少一条这些边。
设两点之间仅当边权为 \(0\) 时有边,则若 \(1\) 可以到达 \(n\),最短路长度为 \(0\),所以问题又变成了删去最少的边使得 \(1\) 不能到达 \(n\)。
于是可以建图,边的容量为 \(1\),求最小割即可。
现在将该问题扩展到最短路长度不为 \(1\) 的情况。设最短路长度为 \(x\),于是我们建立 \(x\) 层图。若第 \(i\) 层有一条 \((x_i,y_i)\) 的边,则从第 \(i\) 层向第 \(i+1\) 层连 \((x_i,y_{i+1})\) 的边,容量为无限大。再将每层的 \(n\) 号点向第一层的 \(n\) 号点连边,容量同样为无限大,求最小割即可得到答案。
考虑为什么可以这么做。设跨层的边表示将路径长度加 \(1\)。若节点 \(1\) 可以到达第 \(i\) 层的 \(n\) 号节点,则经过了 \(i-1\) 条跨层的边,于是该层的最短路长度便为 \(i-1\),显然不满足条件。所以该图的一个割一定满足第 \(i\) 层的最短路长度为 \(i\),于是求出最小割便求出了答案。
ZOJ2587 Unique Attack
省流:判断最小割是否唯一。
思路
我们先对图跑一次最大流,则最大流=最小割。找出剩下的残量网络,并从源点和汇点跑一边dfs。若dfs到了所有点,则最小割唯一,否则不唯一。
\(\text{Part 2.费用流}\)
[HAOI2010]订货
省流:有 \(n\) 天,第 \(i\) 天买一件商品要 \(d_i\) 元,且需要卖出 \(u_i\) 件商品。商品可以多买放进仓库,仓库容量为 \(s\),每件商品过夜要付 \(m\) 元,问达成要求花费最少的钱是多少。
思路
老样子建立超级源点与汇点 \(S,T\)。对于一件商品,我们将 \(S\) 与该商品连边,表示购买的商品数,所以容量为无限大,费用为 \(d_i\)。将商品与 \(T\) 连边,代表该天要求的商品数,所以容量为 \(u_i\),费用为 \(0\)。
因为商品可以存着过夜,所以我们将商品与下面的商品连边,容量为仓库容量 \(s\),费用为 \(m\)。
然后跑费用流没了。
[SDOI2011] 工作安排
省流:有 \(n\) 种产品,每种产品要 \(c_i\) 个。有 \(m\) 个工人,每个工人会做一些产品,每个工人做产品产生的愤怒值跟该工人关于总共做过的产品数的分段函数有关,共有 \(s+1\) 段,每段的愤怒值为 \(w_i\),且 \(w_i\) 单调递增。问最小愤怒值。
思路
网络流方向大致从源点 \(S\) 到产品到工人到汇点 \(T\)。
将 \(S\) 与物品连边,容量为 \(c_i\)。
将物品与能做它的工人连边,容量无限大。
将工人与 \(T\) 连 \(s+1\) 条边,每条边的容量为分段函数一段的长度,费用为该段的愤怒值,因为愤怒值单调递增,所以流一定会先从愤怒值小的流完,满足顺序。
P2223/P1251/P2917[HNOI2001] 软件开发
没错,这题是三倍经验。
其实还有一道一模一样的题P4480,但是那题数据范围太大,把网络流优化掉了。
好像加各种奇奇怪怪的优化又可以用网络流过
又臭又长版:有 \(n\) 天,第 \(i\) 天需要 \(n_i\) 块干净的毛巾,并将返还脏的毛巾,可以在第 \(i\) 天开始前买入干净的毛巾,价格 \(f\)。可以在第 \(i\) 天结束时将脏的毛巾进行清洗,可以对每块毛巾选择花费 \(a\) 天,价格 \(f_a\) 或花费 \(b\) 天,价格 \(f_b\) 的清洗服务(即在 \(a\) 或 \(b\) 天后返还干净的毛巾)。问达成要求花费最少的钱是多少。
思路
建立超级源汇点,考虑将一天拆成给毛巾前和返还脏毛巾后(即干净毛巾与脏毛巾)两个点,称为 \(x,y\)。
源点 \(S\) 表示吐出提供的毛巾,汇点 \(T\) 表示吃掉使用的毛巾。
因为第 \(i\) 天需要使用 \(n_i\) 块毛巾,所以将 \(x\) 与 \(T\) 连边,容量为 \(n_i\),费用为 \(0\)。
因为第 \(i\) 天使用了 \(n_i\) 块毛巾,所以用完后留下了 \(n_i\) 块脏毛巾,将 \(S\) 与 \(y\) 连边,容量为 \(n_i\),费用为 \(0\)。
因为可以随便买毛巾,所以将 \(S\) 与 \(x\) 连边,容量无限大,费用为 \(f\)。
因为毛巾可以使用两种清理服务,所以将 \(y\) 与 \(x+a+1\) 和 \(x+b+1\) 连边,容量无限大(当然可以随便清洗),费用为 \(f_a\) 和 \(f_b\)。
可以发现脏毛巾可以留着下一天再清洗,所以将 \(y\) 与 \(y+1\) 连边,容量无限大,费用为 \(0\)。
然后这题就做完了。
[Wf2011] Chips Challenge
省流:给出一个正方形网格,其中一些格子不能放部件,一些格子已经放了部件。你需要放最多的部件,使得每行每列的部件数都相同,且每行每列的部件数不超过总部件数的 \(\frac{A}{B}\)。
思路
观察到 \(n\le 40\),所以我们可以枚举每行每列的部件数使得满足该条件时总部件数最大。其中部件数最大可以看成先把所有能放的地方全放满,再拿走一些部件。
于是原问题变为给你每行每列限制的部件数,使得删去的部件数最小,很容易想到最小费用最大流。其中最小费用为删去的最小部件数,最大流用来判断合法性。以下先给出建图方式。
建立超级源汇点 \(S,T\)。设先把所有能部件的地方全放满后棋盘第 \(i\) 行的棋子数为 \(a_i\),第 \(j\) 列的棋子数为 \(b_j\)。把每行的点和每列的点分成两部分(二分图)。将 \(S\) 与 \(i\) 连边,容量为 \(a_i\),将 \(j\) 与 \(T\) 连边,容量为 \(b_j\)。将相同的 \(i\) 与 \(j\) 连边,容量为限制的部件数,以上的费用均为 \(0\)。若 \((i,j)\) 可以被拿走,则将 \(i\) 与 \(j\) 连边,容量为 \(1\),费用为 \(1\)。最终跑完最小费用最大流后若从 \(S\) 出发和到达 \(T\) 的边均为满流,则合法,放上的部件数即为总共可以放上的部件数减去最小费用(即为删去的最少部件)。
思考为什么可以这么连边。
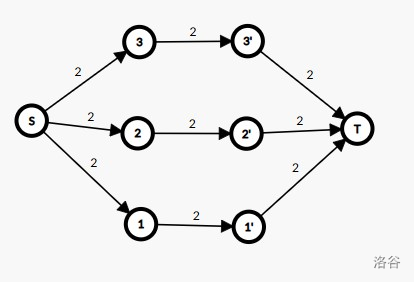
假设网格中没有可以被拿走的部件,那么可以发现仅当每行的部件数,每列的部件数,限制的部件数均相等时才可以跑满流。
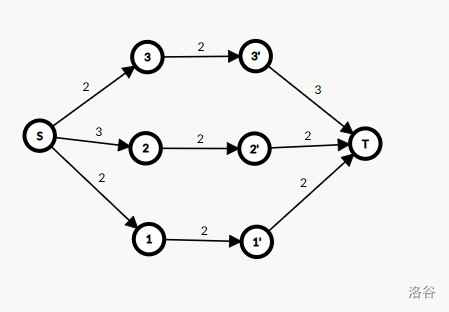
上图中可以发现 \(S\to 2,3'\to T\) 的边显然跑不满,不满足条件,但是若 \((2,3)\) 的部件可以被删除呢?
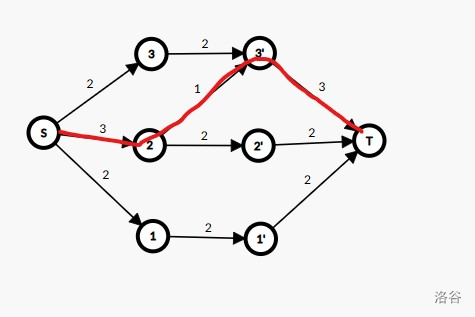
显然,当加上 \(2\to 3'\) 的边时,原图满足了条件。观察红色的一条流。这条流为第 \(2\) 行和第 \(3\) 列的边提供了 \(1\) 的流量,即使得第 \(2\) 行和第 \(3\) 列的部件数减少了 \(1\)。所以选中这条边(删去这个部件)就使得该行和该列的部件数减少了 \(1\),所以我们设这些边的费用为 \(1\),最后的最小费用流得出的答案即为删去的最少边。
[SDOI2017] 新生舞会
省流:给出 \(n,a_{i,j},b_{i,j} \pod{1\le i,j\le n}\)。确定一个长度为 \(n\) 的排列 \(x\),使得 \(c=\frac{\sum_{i=1}^n a_{i,x_i}}{\sum_{i=1}^n b_{i,x_i}}\) 最大。
思路
经典分数规划题。
先考虑一个简单版的题目:给出 \(n,a_i,b_i\pod{1\le i,j\le n}\),从中选择 \(m\) 个数字使得 \(c=\frac{\sum a_i}{\sum b_i}\) 最大。
假设我们知道 \(c\) 的值,则我们可以移项得出:
我们可以发现,随着 \(c\) 的增大,左边柿子可以选出的最小值也会逐渐增大,这一步可以通过贪心选择最小的 \(m\) 项得出。于是我们可以二分 \(c\),当 \(min_l<0\) 时往左取只会让 \(min_l\) 越来越小,所以我们让 \(l=mid\),反之 \(r=mid\)。最后 \(l\) 和 \(r\) 的差值小于一个 \(eps\) 后便可以得到最后的答案。
再来考虑这个问题,可以发现这个问题是差不多的。同样移项可以得到 \(\sum_{i=1}^n (b_{i,x_i}c-a_{i,x_i})=0\)。为了使得左边最小,我们可以建立费用流模型。
我们建立二分图,设左边的点为 \(i\),右边的点为 \(j \ (x_i)\)。将 \(S\) 与 \(i\) 连边,容量为 \(1\)(很显然每个 \(i\) 只能取一个),费用为 \(0\)。将 \(j\) 与 \(T\) 连边,容量为 \(1\),费用为 \(0\),将 \(i\) 与 \(j\) 连边,容量为 \(1\),费用为 \(b_{i,j}c-a_{i,j}\)。其实这就是一个二分图最大匹配问题的网络流建图解法,但是这个图的最大匹配一定为 \(n\),所以最后的最小费用即为该式的最小取值,然后剩下的部分就跟简单版问题一模一样了。
POJ3068/SP4227 "Shortest" pair of paths
省流:带权边有向图上找两条从 \(1\) 到 \(n\) 的不相交路径使得边权和最小。
思路
发现最小费用最大流中最大流可以限制每条边走过的次数,最小费用可以求出最小的边权和,十分的适合写这种题。
因为每条边最多只能走一次,所以我们将原图建出来,容量为 \(1\),费用为边权。
因为要找两条路,所以建立超级源汇点 \(S,T\),\(S\) 向 \(1\) 连边,\(n\) 向 \(T\) 连边,容量为 \(2\),费用为 \(0\)。
跑一遍费用流,若 \(n\to T\) 的这条边没有满流,代表没有找到足够的路径条数,无解。否则最后的最小费用即为答案。
Kaka's Matrix Travels
题意:在正方形矩阵上从 \((1,1)\) 走到 \((n,n)\),总代价为走过的矩阵上的数字之和,并将走过的数字替换成 \(0\)。问走 \(k\) 次获得的最大代价为多少。
思路
这题跟上一题基本是一模一样的,就是有点不一样。
- 求的是最大值
只需将数字取反,将最后得到的答案再取反即可。
- 每个格子只能获得一次代价,但是可以走多次。
我们可以把每个格子进行拆点,在点之间连两条边。第一条是容量为 \(1\),费用为 \(w\) 的边,第二条为容量为无限大,费用为 \(0\) 的点。这样就可以保证第一次走的是可以获得代价的边,之后走的就是没有代价的边,
然后将每个格子向下向右连边,容量同样为无限大,费用为 \(0\)。
最后一样建立超级源汇点 \(S,T\),\(S\) 向 \((1,1)\) 连边,\((n,n)\) 向 \(T\) 连边,容量为 \(k\),费用为 \(0\)。最小费用的相反数即为答案。
POJ3686 The Windy's
省流:有 \(m\) 个工厂,\(n\) 批玩具,第 \(i\) 个玩具在第 \(j\) 个工厂加工需要 \(z_{i,j}\) 小时,一个工厂在加工时不能加工其他玩具,问每个玩具加工用时的平均值最小值为多少。
思路
考虑只有一个工厂时共加工了 \(n\) 个玩具,其中第 \(i\) 个玩具耗时 \(z_i\),那么我们可以知道所有玩具加工时间的平均值为:
也就是:
因此我们将源点与每个玩具连边,将每个工厂拆成 \(n\) 个点,每个点表示的该工厂做的第几个玩具,每个点到汇点连边,容量为 \(1\),费用此时花费的时间,可以通过上面的公式得出。将玩具与工厂连边,容量同样为 \(1\),跑最小费用流即可。
\(\text{Part 3.万物皆可网络流}\)
CF1437C Chef Monocarp
思路
每个时间只能选一个物品,不同的时间选物品有不同的代价,\(n\le 200\),于是直接无脑费用流。
建立经典二分图模型,源点 \(S\) 向每个物品连边,每个时间向汇点 \(T\) 连边,容量为 \(1\),费用为 \(0\)。每个物品向每个时间连边,容量为 \(1\),费用为该时间取出该物品的不美味度。
当菜品最佳时间均为 \(n\) 时时间范围最多取到了 \(\lceil\frac{3}{2}n\rceil\),我取了 \(2n\),需要开 \(3\) 倍空间,需要注意。
CF1426E Rock, Paper, Scissors
思路
最多很好求,只需要贪心让石头尽可能多对剪刀,剪刀尽可能多对布,布尽可能多对石头即可。
最少的呢?我想了半小时没写出来。
于是:
建立二分图模型,将 \(S\) 与 Alice 的石头剪刀布连边,容量为数量,费用为 \(0\),将 Bob 的同理与 \(T\) 连边。
将 Alice 与 Bob 可能赢的组合连费用为 \(1\),容量无限大的边,反之连费用为 \(0\),容量无限大的边。
跑一遍费用流,于是不带一点脑子A了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号