UVA1104 芯片难题 Chips Challenge

题意

给出一个正方形网格，其中一些格子不能放部件，一些格子已经放了部件。你需要放最多的部件，使得每行每列的部件数都相同，且每行每列的部件数不超过总部件数的 \(\frac{A}{B}\)。

思路

观察到 \(n\le 40\)，所以我们可以枚举每行每列的部件数使得满足该条件时总部件数最大。其中部件数最大可以看成先把所有能放的地方全放满，再拿走一些部件。

于是原问题变为给你每行每列限制的部件数，使得删去的部件数最小，很容易想到最小费用最大流。其中最小费用为删去的最小部件数，最大流用来判断合法性。以下先给出建图方式。

建立超级源汇点 \(S,T\)。设先把所有能放部件的地方全放满后棋盘第 \(i\) 行的棋子数为 \(a_i\)，第 \(j\) 列的棋子数为 \(b_j\)。把每行的点和每列的点分成两部分（二分图）。将 \(S\) 与 \(i\) 连边，容量为 \(a_i\)，将 \(j\) 与 \(T\) 连边，容量为 \(b_j\)。将相同的 \(i\) 与 \(j\) 连边，容量为限制的部件数，以上的费用均为 \(0\)。若 \((i,j)\) 可以被拿走，则将 \(i\) 与 \(j\) 连边，容量为 \(1\)，费用为 \(1\)。最终跑完最小费用最大流后若从 \(S\) 出发和到达 \(T\) 的边均为满流，则合法，放上的部件数即为总共可以放上的部件数减去最小费用（即为删去的最少部件）。

思考为什么可以这么连边。

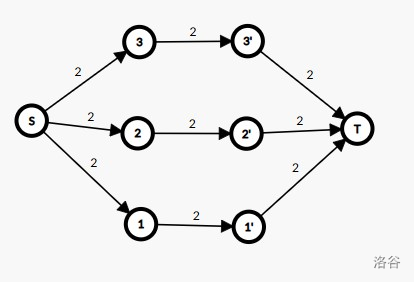
假设网格中没有可以被拿走的部件，那么可以发现仅当每行的部件数，每列的部件数，限制的部件数均相等时才可以跑满流。

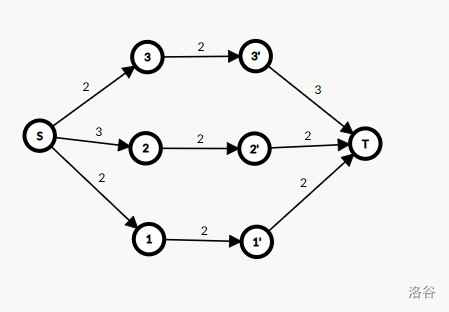
上图中可以发现 \(S\to 2,3'\to T\) 的边显然跑不满，不满足条件，但是若 \((2,3)\) 的部件可以被删除呢？

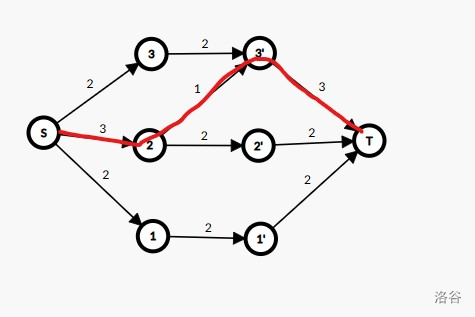
显然，当加上 \(2\to 3'\) 的边时，原图满足了条件。观察红色的一条流。这条流为第 \(2\) 行和第 \(3\) 列的边提供了 \(1\) 的流量，即使得第 \(2\) 行和第 \(3\) 列的部件数减少了 \(1\)。所以选中这条边（删去这个部件）就使得该行和该列的部件数减少了 \(1\)，所以我们设这些边的费用为 \(1\)，最后的最小费用流得出的答案即为删去的最少边。

代码

#include<bits/stdc++.h>
using namespace std;
namespace mf{
	const int N=105,INF=0x3f3f3f3f;
	struct node{int x,w,c,rev;};
	vector<node> t[N];
	int dis[N],flow[N],maxflow,mincost;
	node *pre[N];
	bool vis[N];
	int n,m,S,T;
	void add(int x,int y,int w,int c){
		t[x].push_back({y,w,c,t[y].size()});
		t[y].push_back({x,0,-c,t[x].size()-1});
	}
	bool spfa(){
		memset(dis,0x3f,sizeof(dis));
		memset(vis,0,sizeof(vis));
		queue<int> q;
		dis[S]=0,vis[S]=true,flow[S]=INF,q.push(S);
		while(!q.empty()){
			int u=q.front();
			q.pop(),vis[u]=false;
			for(node&v:t[u]){
				if(v.w&&dis[v.x]>dis[u]+v.c){
					dis[v.x]=dis[u]+v.c;
					flow[v.x]=min(flow[u],v.w);
					pre[v.x]=&v;
					if(!vis[v.x])
						vis[v.x]=true,q.push(v.x);
				}
			}
		}
		return dis[T]!=INF;
	}
	void upd(){
		int x=T;
		while(x!=S){
			node *i=pre[x];
			i->w-=flow[T];
			t[i->x][i->rev].w+=flow[T];
			x=t[i->x][i->rev].x;
		}
		maxflow+=flow[T],mincost+=flow[T]*dis[T];
	}
	pair<int,int> ek(){
		memset(flow,0,sizeof(flow));
		maxflow=mincost=0;
		while(spfa()) upd();
		return {maxflow,mincost};
	}
}
int n,A,B,a[45],b[45];
struct node{
	int x,y;
};
vector<node> add;
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(),cout.tie();
	for(int T=1;T;T++){
		add.clear();
		memset(a,0,sizeof(a));
		memset(b,0,sizeof(b));
		cin>>n>>A>>B;
		if(!n&&!A&&!B) break;
		mf::n=2*n+2,mf::S=2*n+1,mf::T=2*n+2;
		char st;
		int tot=0,tot2=0,ans=-1;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				cin>>st;
				if(st!='/')
					tot++,a[i]++,b[j]++;
				if(st=='.')
					tot2++,add.push_back({i,j});
			}
		}
		for(int i=0;i<=n;i++){
			for(int j=1;j<=mf::n;j++)
				mf::t[j].clear();
			for(int j=1;j<=n;j++)
				mf::add(mf::S,j,a[j],0),mf::add(j+n,mf::T,b[j],0),mf::add(j,n+j,i,0);
			for(node v:add)
				mf::add(v.x,n+v.y,1,1);
			pair<int,int> res=mf::ek();
			bool can=1;
			for(mf::node v:mf::t[mf::S])
				if(v.w!=0){can=0;break;}
			for(mf::node v:mf::t[mf::T])
				if(mf::t[v.x][v.rev].w!=0){can=0;break;}
			if(can&&i<=(tot-res.second)*1.0*A/B)
				ans=max(ans,tot2-res.second);
		}
		if(ans==-1)
			cout<<"Case "<<T<<": impossible"<<endl;
		else
			cout<<"Case "<<T<<": "<<ans<<endl;
	}
	return 0; 
}