[ARC193A] Complement Interval Graph

\[ARC193A\] Complement Interval Graph

题意

给出 \(n\) 个数字区间 \([l_i,r_i]\)（表示从 \(l_i\) 到 \(r_i\) 的所有整数）以及每个区间的权值 \(w_i\)，两个区间可以互相到达仅当两个区间没有交集。有 \(q\) 组询问，每次询问给出 \(x,y\)，问从第 \(x\) 个区间到第 \(y\) 个区间所经过的所有区间（包括 \(x,y\)）的最小权值和。

思路

考虑分类讨论。

1. 两个区间没有交集。

这时 \(x\) 可以直接到达 \(y\)，答案即为 \(w_x+w_y\)。

2. 两个区间有交集，考虑以下两种情况。

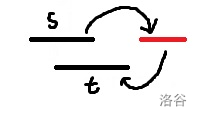
这时可以找到一个不跟 \(x,y\) 之中任意一个区间相交的最小权值区间 \(k\)，答案即为 \(w_x+w_k+w_y\)。

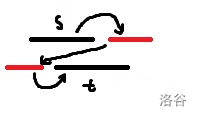
可以发现当两个区间不存在包含关系时，还可以选择在右端点最小的区间右边找到一个不相交的最小权值区间 \(k_1\)，在左端点最大的区间左边找到一个不相交的最小权值区间 \(k_2\)，此时答案即为 \(w_x+w_{k_1}+w_{k_2}+w_y\)。

可以证明，不存在除了以上两种情况以外更优的走法，因为对于任意一种合法走法总是可以优化为中间经过不超过两个区间的走法。

快速找到不跟某个区间相交的最小区间很简单。对于两区间 \([l_1,r_1]\) 与 \([l_2,r_2]\) 仅当 \(r_1<l_2\) 或 \(r_2<l_1\) 时不相交，于是对区间的 \(l\) 和 \(r\) 分别排序，并对每个 \(i\) 预处理出 \(r\) 不大于 \(i\) 与 \(l\) 不小于 \(i\) 的区间的权值最小值即可。

代码

（赛时写蠢了，没看到 \(1\le L,R\le 2N\)，参考价值不大）

code