[ABC378F] Add One Edge 2

[ABC378F] Add One Edge 2

题意

给定一棵树，你需要加入一条边使树成为基环树（即包含恰好一个环的无向连通图），问有多少种加边的方案使环上的点度数都为 \(3\)。

思路

若两个点 \(x,y\) 之间连边后满足条件，即环上的点度数都为 \(3\)，则一定满足点 \(x,y\) 的度数为 \(2\)，\(x,y\) 的简单路径经过的点（除了这两个点）的度数为 \(3\)，因为 \(x,y\) 连边后它们的度数会变成 \(2+1=3\)，就满足了环上的点度数都为 \(3\)。

有了这个思路后，我们可以找到所有度数为 \(3\) 的点并按照原图合并，操作后便会形成一些连通块，然后对于每个连通块找到相连的度数为 \(2\) 的点，这些点之间的任意两点连边都可以形成满足条件的环，因为它们之间的简单路径只会经过该连通块中的点（除了这两个点），且连通块中的点在原树上度数都为 \(3\)。设这些点共有 \(x\) 个，则它们两两连边可以产生 \(\frac{x\times (x-1)}{2} \pod{x\ge 2}\) 种方案，将所有连通块产生的方案加起来即可得到方案数。

比如对于样例 \(3\)，该样例输入为：

15
1 15
11 14
2 10
1 7
9 8
6 9
4 12
14 5
4 9
8 11
7 4
1 13
3 6
11 10

这棵树的形态如下：

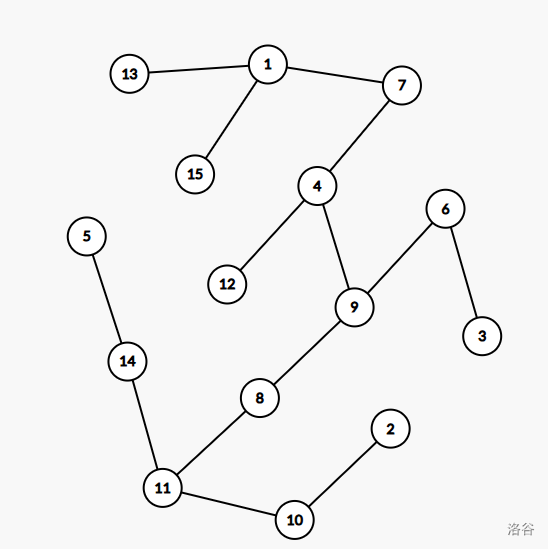
找到所有度数为 \(3\) 的点。

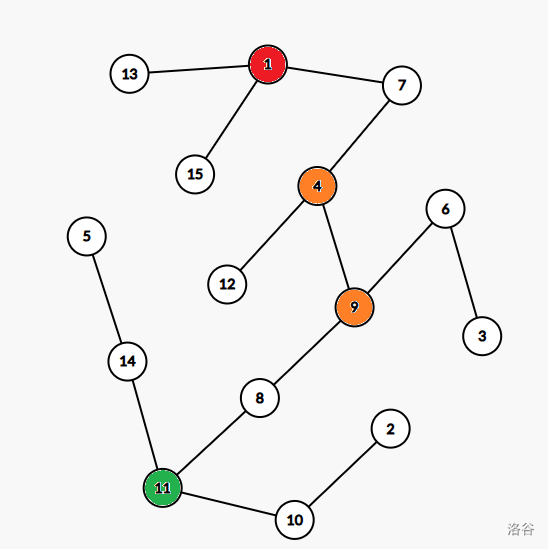
可以发现，这些点构成了 \(3\) 个连通块，我们对于每个连通块分别处理。

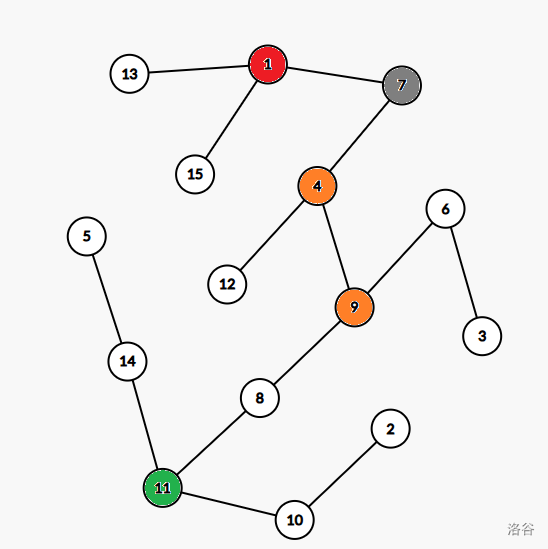
对于红色的连通块，有 \(1\) 个度数为 \(2\) 的点相连，所以这个连通块的贡献为 \(0\)。

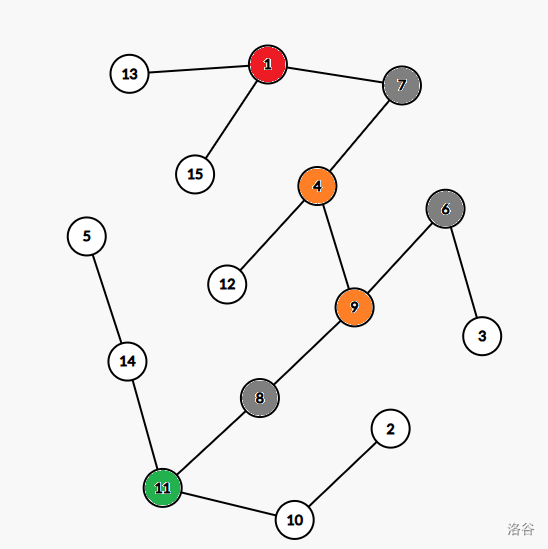
对于橙色的连通块，有 \(3\) 个度数为 \(2\) 的点相连，所以这个连通块的贡献为 \(3\)。

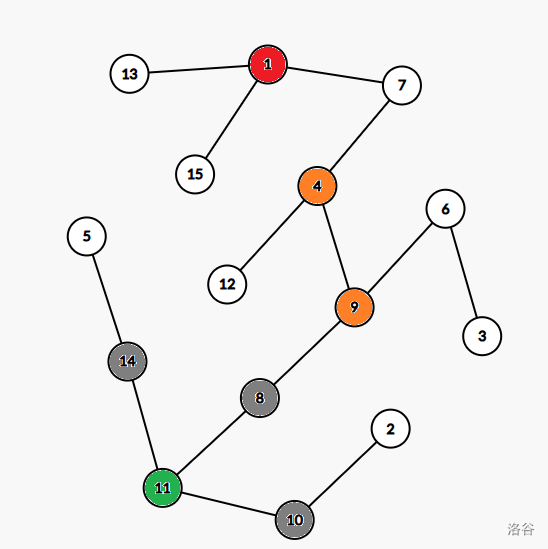
对于绿色的连通块，有 \(3\) 个度数为 \(2\) 的点相连，所以这个连通块的贡献为 \(3\)。

最终的答案即为 \(3+3=6\)。

代码

写的很丑，参考意义不大（

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,d[400005],fa[400005],ans;
bool vis[400005],ist[400005];
int find(int x){
	if(fa[x]!=x)fa[x]=find(fa[x]);
	return fa[x];
}
void uni(int x,int y){
	int p1=find(x),p2=find(y);
	if(p1!=p2)
		fa[p1]=p2;
}
vector<int> t[400005],t2[400005];
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	cin>>n;
	for(int i=1;i<=n;i++)
		fa[i]=i;
	for(int x,y,i=1;i<n;i++){
		cin>>x>>y;
		t[x].push_back(y);
		t[y].push_back(x);
	}
	for(int i=1;i<=n;i++)
		if(t[i].size()==3){
			for(int v:t[i])
				if(t[v].size()==3)
					uni(i,v);
		}
	for(int i=1;i<=n;i++)
		if(t[i].size()==3)
			ist[find(i)]=true;
	for(int i=1;i<=n;i++){
		for(int v:t[i])
			if(find(i)!=find(v))
				t2[find(i)].push_back(find(v));
	}
	for(int i=1;i<=n;i++){
		if(!ist[i]) continue;
		int cnt=0;
		for(int v:t2[i]){
			if(t2[v].size()==2)
				cnt++;
		}
		if(cnt>=2)
			ans+=cnt*(cnt-1)/2;
	}
	cout<<ans<<endl;
	return 0;
}