[模板] 前缀建边

例题：Riddle

对于本题而言，每个点有两种状态：选或不选。

同时题目又给出限制条件：点集内只能选一个点，一条边上至少选一个点

这也太明显了吧

所以就是在点集内，若选择某个点则另外的点不能选；一条边上，若不选某个点，则另一个点必选。此时已经很显然了，2-SAT建边跑强连通分量判断是否矛盾，完事

但是如果直接暴力建边就会总有大数据MLE或TLE！

而其根本原因就在点集内的建边

for(int i=1;i<=k;i++)
{
    scanf("%d",&t);
    for(int j=1;j<=t;j++)scanf("%d",&a[j]);
    for(int j=1;j<=t;j++)
    {
        for(int l=1;l<=t;l++)
             if(l==j)continue;
        else add((a[j]-1)*2,(a[l]-1)*2+1);
    }
}

快乐超限

N^2N2的算法让人难以接受，时间空间过大，为解决这个问题必须优化点集内建边算法

这是我们原来的建图方式，朴素但是有效好歹92分

如何优化呢？关键就在于缩小N^2N2的计算量，而要完成这一步，关键是减少建边的数量（或者说优化建边的方式）

2-SAT里变量两种状态的点是关键，不可能直接在这2N2N个点之上优化。自然而然得，我们应当新建若干点作为媒介使新图拥有原来的性质，而这2N2N个点的地位等价（感觉一下？），自然应当新建2N2N个点一一对应（连边）

为保持原来点的性质不变，出点继续出，入点继续入

然后自然而然得，我们可以转移边

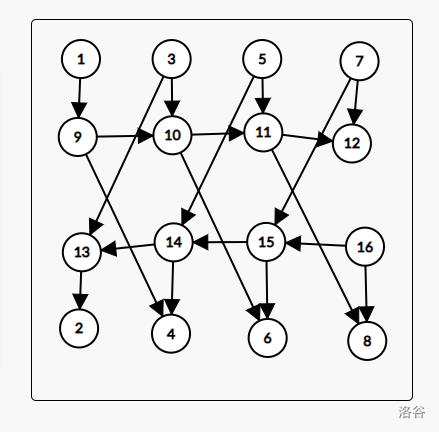
对于这幅图，我们容易发现没错非常容易，9-16，10-16，11-16这三条边可以变成9-10，10-11，11-16这样的三条边，而同时9-10还可以用于9-15，10-15到9-10，10-15的转换。所以经过这样的转化，我们能得到这张图

但是这张图存在致命的错误：出现了1-9-14-13-2，1-9-10-13-2之类的错误线路，为了调整这种线路，我们将9-14调整为9-4，10-13调整为3-13（保持9-10，14-13之类的由有利边仍然存在），类似操作后，有了这张图

此时图形已经符合原图的所有性质，但是为了便于进行循环操作，我们对其微调(也就4条边），得到这张图（也就是程序得到的图）

int cntt=2*n;
for(int j=1;j<=k;j++)
{
    scanf("%d",&t);
    for(int i=1;i<=t;i++)
    {
        scanf("%d",&a[i]);
        pre[a[i]][0]=++cntt;//新建点
        pre[a[i]][1]=++cntt;//新建点
        add((a[i]-1)*2,pre[a[i]][0]);
        add(pre[a[i]][1],(a[i]-1)*2+1);
    }
    for(int i=2;i<=t;i++)
    {
        int d1=a[i-1],d2=a[i];
        add(pre[d1][0],pre[d2][0]);
        add(pre[d2][1],pre[d1][1]);
        add(pre[d1][0],(d2-1)*2+1);
        add((d2-1)*2,pre[d1][1]);
    }
}

所以就可以轻松（？）通过

#include<cstdio>
#include<cstring>
#include<string>
#include<stack>
#include<iostream>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=10010000,mod=1e9+7;
struct Edge{
    int pre,to;
}edge[WR];
int n,m,k,w;
int a[WR];
int head[WR],tot=0;
int ipt[WR],low[WR],cnt=0;
int id[WR],sze[WR],point;
int pr[WR][2];
bool instk[WR];
stack<int>s;
int read(){
    int s=0,w=1;
    char ch=getchar();
    while(ch>'9'||ch<'0'){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        s=(s<<3)+(s<<1)+ch-48;
        ch=getchar();
    }
    return s*w;
}
void add(int u,int v){
    edge[++tot].pre=head[u];
    edge[tot].to=v;
    head[u]=tot;
}
void tarjan(int u){
    low[u]=ipt[u]=++cnt;
    s.push(u);instk[u]=true;
    for(int i=head[u];i;i=edge[i].pre){
        int v=edge[i].to;
        if(!ipt[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }else if(instk[v]){
            low[u]=min(low[u],ipt[v]);
        }
    }
    if(low[u]==ipt[u]){
        int v;
        point++;
        do{
            v=s.top(),s.pop();
            instk[v]=false;
            sze[point]++;
            id[v]=point;
        }while(v!=u);
    }
}
signed main(){
    n=read(),m=read(),k=read();
    for(int i=1;i<=m;i++){
        int u=read(),v=read();
        add((u-1)*2+1,(v-1)*2);
        add((v-1)*2+1,(u-1)*2);
    }
    int num=n*2;
    for(int i=1;i<=k;i++){
        int t=read();
        for(int j=1;j<=t;j++){
            a[j]=read();
            pr[a[j]][0]=++num;
            pr[a[j]][1]=++num;
            add((a[j]-1)*2,pr[a[j]][0]);
            add(pr[a[j]][1],(a[j]-1)*2+1);
        }
        for(int j=2;j<=t;j++){
            add(pr[a[j-1]][0],pr[a[j]][0]);
            add(pr[a[j]][1],pr[a[j-1]][1]);
            add(pr[a[j-1]][0],(a[j]-1)*2+1);
            add((a[j]-1)*2,pr[a[j-1]][1]);
        }
    }
    for(int i=0;i<=num;i++){
        if(!ipt[i]) tarjan(i);
    }
    bool flag=true;
    for(int i=1;i<=n;i++){
        if(id[(i-1)*2]==id[(i-1)*2+1]){
            flag=false;
            break;
        }
    }
    if(flag) printf("TAK");
    else printf("NIE");
    return 0;
}