hdu4044（树形dp，好题）

src：http://acm.hdu.edu.cn/showproblem.php?pid=4044

 

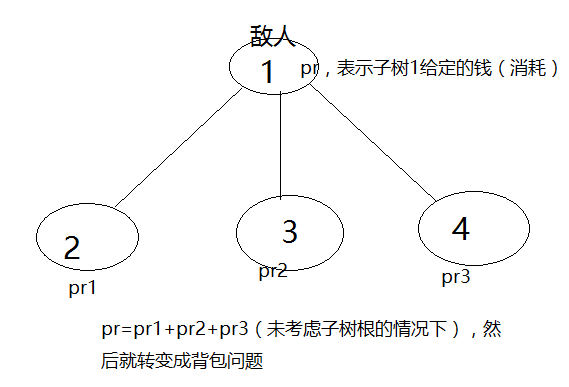
dp[u][i]为u不选的时候花i元的最优解，这题考虑dp[ u ][ i ]时对于子树根u选不选分开讨论，一种方法是定义状态为dp[ u ][ i ][ 0/1 ]分别表示选/不选，但是这样转移方程不好写，然后就是另一种全新的姿势，如上定义，

定义dp[u][i]为u不选的时候花i元的最优解

预处理一个w[u][i]表示u结点花i元最多能获得的权值

考虑一个叶子结点：dp[u][i]=w[u][i]

考虑一个非叶子结点不选时候:每一个儿子v加进来的时候，状态都分裂为dp[v][k]和dp[u][j-k]

对于每一个枚举的k来说，答案是min(dp[v][k],dp[u][j-k]) 维护这个答案的最大值就是dp[u][j]

考虑完u不选的情况后，再对u单独做一次背包，枚举u的花费，取个最优值就是答案

ac代码：

#include <iostream>
#include<stdio.h>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<functional>
#include<utility>
#include<string>
#include<string.h>
#include<vector>
#include<iomanip>
#include<stack>
#include<queue>
using namespace std;
#define FOR(i,a,b) for(int i=a;i<=b;i++)
#define Max(a,b) a=max(a,b)
#define Min(a,b) a=min(a,b)
const int inf=0x3f3f3f;
#define siz 1005
int n,m,head[siz],Enum=0;
struct{
    int to,ne;
}edge[siz<<1];
int chose[siz][205],dp[siz][300];

void init()
{
    Enum=0;
    memset(head,-1,sizeof(head));
    memset(dp,0x3f,sizeof(dp));
    memset(chose,0,sizeof(chose));
}
void add_edge(int a,int b)
{
    edge[Enum].to=b;
    edge[Enum].ne=head[a];
    head[a]=Enum++;
}
void dfs(int u,int fa)
{
    int f=0;
    for(int i=head[u];i!=-1;i=edge[i].ne){
        int v=edge[i].to;
        if(v==fa)continue;
        dfs(v,u);
        f=1;
        for(int j=m;j>=0;j--){
            int tmp=0;
            for(int k=0;k<=j;k++)tmp=max(tmp,min(dp[v][k],dp[u][j-k]));
            dp[u][j]=tmp;//dp初始化为inf，上面这条转移方程就表示tmp选择一条可考虑的最小消耗的那条路！没考虑
        }                //所有子树时（没子树）攻破子树的消耗为inf
    }
    if(f==0){
        for(int i=0;i<=m;i++)dp[u][i]=chose[u][i];
        return;
    }
    for(int i=m;i>=0;i--){
        for(int j=0;j<=i;j++){
            dp[u][i]=max(dp[u][i],dp[u][i-j]+chose[u][j]);
        }
    }
}

int main()
{
    std::ios::sync_with_stdio(false);
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        init();
        int a,b,k;
        for(int i=1;i<n;i++){
            scanf("%d %d",&a,&b);
            add_edge(a,b);add_edge(b,a);
        }
        scanf("%d",&m);
        for(int i=1;i<=n;i++){
            scanf("%d",&k);
            for(int j=1;j<=k;j++){
                scanf("%d %d",&a,&b);
                chose[i][a]=max(chose[i][a],b);
            }
            for(int j=1;j<=m;j++)chose[i][j]=max(chose[i][j],chose[i][j-1]);
        }
        dfs(1,-1);
        //for(int i=0;i<=m;i++){printf("%d ",dp[1][m]);}printf("\n");system("pause");
        printf("%d\n",dp[1][m]);
    }
    return 0;
}