回溯算法解决0/1背包问题

回溯法采用深度搜索+剪枝生成搜索树

回溯法在确定了解空间的结构后，从根结点出发，以深度优先的方式搜索整个解空间，此时根结点成为一个活结点，并且成为当前的扩展结点。每次都从扩展结点向纵向搜索新的结点，当算法搜索到了解空间的任一结点，先判断该结点是否肯定不包含问题的解（是否还能或者还有必要继续往下搜索），如果确定不包含问题的解，就逐层回溯；否则，进入子树，继续按照深度优先的策略进行搜索。当回溯到根结点时，说明搜索结束了，此时已经得到了一系列的解，根据需要选择其中的一个或者多个解即可。

 

 

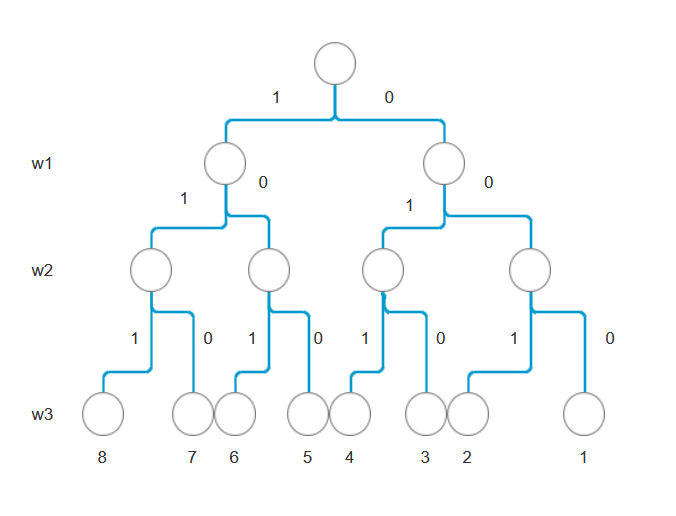
 如图所示，对三个物品w1，w2，w3进行回溯法时，当三个物品都不选，结果为1，得到一个结果和一个最优值，此时回溯至上一个节点w2，即第一个不选，第二个不选，但是第三个选，则结果来到了2，得到一个新的结果和最优值，此时与之前记录的结果和最优值进行比较，留下最优值较大结果，接着，回溯至节点w1，即第一个不选，但是第二个选，则此时又会有两个选择，即第三个选，和第三个不选，同理判断最优值的大小取其大，但有一点需要注意，以上的所有选择都是建立在一个前提，即所选择的物品重量之和均小于等于背包容量的，这是整个回溯法的约束条件，当选择物品后容量大于了背包容量，则要自动抛弃该选择，并进入下一层回溯。

 

回溯法解决问题基本步骤有三

一 建立模型，设置物品，背包，物品数量，物品价值，物品重量等参数

二 寻找约束条件，即物品总重量不应该超过背包总容量，且装入背包的物品总价值应该尽可能为最大

三 构造一个最优值变量并对每一次回溯结果进行比对，如果与之前存入的最优值相比为大，则将其覆盖替换

 

回溯法解决0/1背包问题核心代码如下所示

 

package com.ccunix.shop.util;

/**
 * 给定n种物品和一背包。物品i的重量是wi，其价值为pi，背包的容量为C。 问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?
 * 
 * @author fulisha
 *
 */
public class test1 {
 
    static int BestValue = 0; // 最优值；当前的最大价值，初始化为0
    static int[] BestX; // 最优解；BestX[i]=1代表物品i放入背包，0代表不放入
    //
    static int CurWeight = 0; // 当前放入背包的物品总重量
    static int CurValue = 0; // 当前放入背包的物品总价值
    static int N = 3;// 物品数量
    static int C = 9;// 物品的总容量
    static int W[] = { 1, 9, 4, }; // 每个物品的重量
    static int v[] = { 2,5,3,};// 每个物品的价值
    static int x[] = { 0, 0, 0};// x[i]=1代表物品i放入背包，0代表不放入
 
    public static int backtrack(int t) {
        // 如果是子节点 当前价值和最佳价值做判断 保存最佳价值
        if (t > N - 1) {
            if (CurValue > BestValue) {
                BestValue = CurValue;
            }
            return BestValue;
        }
        // 如果不是子节点 对子节点进行遍历
        else {
            // 就两种情况 取或不取 用0/1表示
            for (int i = 0; i <= 1; i++) {
                x[t] = i;
                if (i == 0) {
                    // 如果是不取 就不需要进行判断 直接到下一个节点
                    backtrack(t + 1);
                } else
                // 放入背包就进行约束条件 判断放入背包的东西是否合法
                {
                    if (CurWeight + W[t] <= C) {
                        CurWeight += W[t];
                        CurValue += v[t];
                        // 当东西装进入背包后你可以进行对下个商品的判断了
                        backtrack(t + 1);
                        //能执行以下两个语句就说明你回溯到了上一个节点 所以你就需要恢复现场 把你刚刚拿的东西退出来 我们要冲上一个节点又要重新来遍历 如果不减你就会多加一遍 
                        CurWeight -= W[t];
                        CurValue -= v[t];
                    } 
                }
            }
        }
        return BestValue;
    }
 
    public static void main(String[] args) {
        backtrack(0);
        System.out.println(BestValue);
        
    }
 
}

 根据上述代码，即可对0/1背包问题进行回溯法分析，值得注意和讨论的是该代码段中的这两行代码：

CurWeight -= W[t];
CurValue -= v[t];

 

这两行代码的注释意思是：能执行以下两个语句就说明你回溯到了上一个节点 所以你就需要恢复现场 把你刚刚拿的东西退出来 我们要回到上一个节点又要重新来遍历 如果不减你就会多加一遍 ，但如果只是根据注释理解很容易陷入一个误区，即如果我已经回溯到了上一个节点，那么代码所执行的应该是递归的代码部分，这两句话是写在递归语句之后，应该不在递归范围之内，那么为什么还是需要执行呢？后来提出了一个设想，即当回溯到最后一个节点时，代码是需要顺序执行的，所以就需要接着执行这两句进行恢复，但是从代码中可以很容易看出，当回溯到最后一个节点时，保存最优值后代码就会直接进行返回值并在主函数中打印了，所以根本也就不需要顺序执行了，那么难道这两句话是没有用的吗？很明显并不是，我在多次尝试和设想之后找到了一个可以自圆其说的执行顺序：即当执行到递归语句时，该程序段会进行分支，一条支干会正常进行递归算法的编译和执行，但同时还会有另一条分支会继续顺序执行后面的语句，而这里请注意，执行递归算法的支干中同样也有着这两句代码！所以整个流程就变得十分清晰了，递归下一级——恢复上一级+递归下一级——恢复上一级+递归下一级……直到递归到最后一个节点，即第一个物品，以上，就是利用回溯法解决0/1背包问题的我的论点和过程。