📊终于有人把softmax和sigmoid的区别说清楚了！！！

最近在做业务分类预测时，遇到单标签和多标签的分类问题，决定好好扒一扒这个softmax和sigmoid~

首先是应用场景的区别。sigmoid更适合多标签分类（multi-label classification），而softmax适用于单标签多分类（multi-class classification）。在多标签场景中，一个样本可以同时属于多个类别，这时每个类别的判断是独立的。而在单标签场景中，所有类别是互斥的。

第二个重要区别是输出特性。sigmoid对每个输出节点独立计算，输出值在0-1之间但总和不为1。而softmax的所有输出值之和严格为1，形成一个概率分布。

第三个区别是模型结构不同。使用sigmoid时，最后一层神经元数量等于标签类别数；而使用softmax时，神经元数量等于类别总数。这也是为什么在二分类问题中，softmax需要两个神经元而sigmoid只需要一个。

第四点就是在数学特性上，两者的梯度行为也不同。sigmoid在极端值区域会出现梯度消失问题，而softmax在所有区域都有较好的梯度特性。

还有一些进阶区别：在注意力机制中，softmax能更好地表达全局相对关系；在分布式训练中，sigmoid可以异步计算而softmax需要全局同步。（这点也可以和第二点结合起来，因为sigmoid是独立计算所以可以异步；而softmax依赖全部输入所以需要全局同步）

为了更直观地展示区别，使用表格对比和示例场景。

⚙️1、核心原理与输出特性对比

维度	Sigmoid	Softmax
数学定义	单变量函数：${\sigma(z)=\frac{1}{1+e^{-z}} } $	多变量函数：${\sigma(z)_j= \frac{e^{-z_j}}{\sum_k e^{z_k} } } $
输出范围	单值概率：$p \in (0,1) $	概率向量：$p \in (0,1)^k, \sum p_j =1 $
独立性	各节点独立计算概率	概率相互关联，分母依赖所有输入值
分布假设	两点分布（伯努利分布）	多项分布（类别分布）
场景例子	可以同时输出"战争片"和"国产片"标签	只能输出单一类别如"动作片"

关键区别：Sigmoid建模单个类别的概率（如“是/否”），而Softmax建模互斥类别的联合概率分布（如“猫/狗/鸟”三选一）

⚙️ 2、应用场景与网络设计差异

1. 任务类型

Sigmoid适用场景：

• 多标签分类（Multi-label Classification）：
• 样本可同时归属多个类别（如电影标签：战争片+国产片）。
• 二分类输出层：神经元数=1，输出单节点概率（如垃圾邮件检测）。

Softmax适用场景：

• 单标签多分类（Multi-class Classification）：
• 样本仅属唯一类别（如MNIST手写数字识别，10类互斥）。
• 注意力机制权重分配：强制权重和为1（如Transformer的Attention）。

2. 网络结构设计

函数类型	输出层神经元数	损失函数	典型案例
Sigmoid	等于标签数	Binary Cross-Entropy	胸部X光诊断（肺炎/脓肿/正常并存）
Softmax	等于类别总数	Categorical Cross-Entropy	鸢尾花分类（Setosa/Versicolor/Virginica三选一）

✅ 二分类特殊说明：

理论上二者等价，但实现不同：
Sigmoid：输出层1个神经元，计算P(Y=1)，P(Y=0)=1-P(Y=1)
Softmax：输出层2个神经元，计算P(Y=1)和P(Y=0)
实践建议：框架实现差异可能影响梯度传播稳定性，优先推荐Softmax。

📈 三、数学特性与优化挑战

特性	Sigmoid	Softmax
梯度行为	饱和区梯度消失（$	z
稀疏性	可独立输出多个高概率标签	天然压制非最大类，输出稀疏（仅1-2个显著概率）
计算效率	支持异步分布式计算（无需全局同步）	需同步所有节点值（分布式训练通信开销大）

⚠️ Softmax的局限性：

在超多类别（如百万级词表）场景中，全局归一化计算昂贵，可采用分层Softmax或采样方法优化。

❌ 四、常见误区与避坑指南

• 误区：多分类可用多个Sigmoid替代Softmax

错误原因：Sigmoid输出概率独立，可能出现P(猫)+P(狗)>1，违背概率公理。
正确做法：互斥类别必须用Softmax。

• 误区：二分类优先选Sigmoid因更简单

实验证据：在PyTorch/TF中，Softmax的二分类收敛稳定性更优（梯度传播更均衡）

• 误区：注意力机制必须用Softmax

最新研究：Sigmoid在某些稀疏注意力场景可替代Softmax，减少指数计算量

总结来说就是：

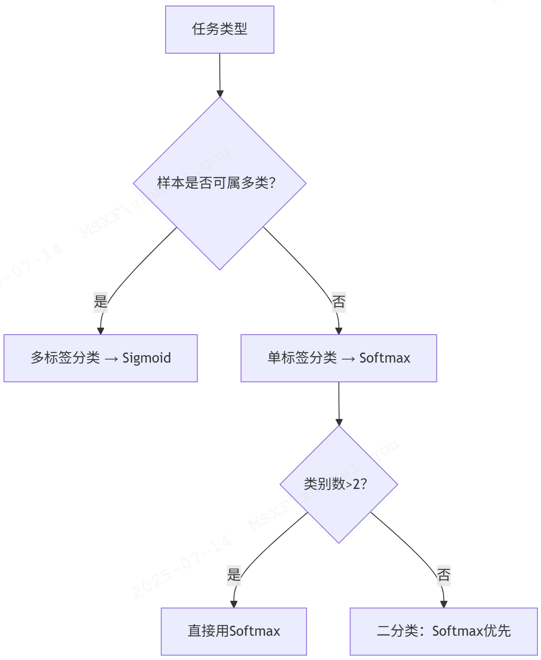
建议根据任务本质选择函数，避免技术误用导致模型性能下降。

对数学细节感兴趣的同学可延伸阅读论文《Sigmoid Gating vs Softmax Gating in MoE》(2024)