实验3

一.实验任务1

实验代码：

#include <stdio.h>

char score_to_grade(int score);  // 函数声明

int main() {
    int score;
    char grade;

    while(scanf("%d", &score) != EOF) {
        grade = score_to_grade(score);  // 函数调用
        printf("分数: %d, 等级: %c\n\n", score, grade);
    }

    return 0;
}

// 函数定义
char score_to_grade(int score) {
    char ans;

    switch(score/10) {
    case 10:
    case 9:   ans = 'A'; break;
    case 8:   ans = 'B'; break;
    case 7:   ans = 'C'; break;
    case 6:   ans = 'D'; break;
    default:  ans = 'E';
    }

    return ans;
}

程序运行结果截图：

解答1：函数的功能是对学生的成绩进行等级的评判。形参类型是整形，返回值类型是字符型。

解答2：修改后的代码将break语句删除了，由于switch不具有if的‘强制性’，因此在没有break时，哪怕它找到了对应的分支，仍然也会执行该分支之后的行为语句，在这里体现为对ans的多次赋值，直到最后一次default将ans赋值为E,因此，不管输入的分数为多少，最终都会被函数返回E等级。再就是，修改后的语句是用双引号引导的等级字符，意味着这里的等级是字符串类型，而返回值ans定义为char字符型，这会引起程序的报错。

二.实验任务2

实验代码：

#include <stdio.h>

int sum_digits(int n);  // 函数声明

int main() {
    int n;
    int ans;

    while(printf("Enter n: "), scanf("%d", &n) != EOF) {
        ans = sum_digits(n);    // 函数调用
        printf("n = %d, ans = %d\n\n", n, ans);
    }

    return 0;
}

// 函数定义
int sum_digits(int n) {
    int ans = 0;

    while(n != 0) {
        ans += n % 10;
        n /= 10;
    }

    return ans;
}

程序运行结果截图：

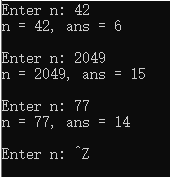
解答1：函数的功能是将用户输入的整数的各个数位上的数字求和。

解答2：修改后的函数代码用了递归的思路来实现同样的功能，原代码用的是循环的思路来实现。循环方法类似于逐个击破的思想，将各个位数上的数字拿到后再做处理。而递归更像是大事化小，小事化了的思想。将原问题不断地拆解成更简单一些的问题，直到问题变为一个非常简单易求解的问题，然后在逐层往上返回结果，就像积木拼装一样，最终得到了整个问题的答案。

if(n < 10)
        return n;

return sum_digits(n / 10) + n%10;

三.实验任务3

实验代码：

#include <stdio.h>

int power(int x, int n);    // 函数声明

int main() {
    int x, n;
    int ans;

    while(printf("Enter x and n: "), scanf("%d%d", &x, &n) != EOF) {
        ans = power(x, n);  // 函数调用
        printf("n = %d, ans = %d\n\n", n, ans);
    }
    
    return 0;
}

// 函数定义
int power(int x, int n) {
    int t;

    if(n == 0)
        return 1;
    else if(n % 2)
        return x * power(x, n-1);
    else {
        t = power(x, n/2);
        return t*t;
    }
}

程序运行截图：

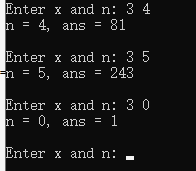
解答1：函数的功能是计算x的n次方的值

解答2：该函数是递归函数，递归模式为：

      ⌈  x^n/2  * x^n/2 , n为偶数

xⁿ=|

      ⌊ x * x^n-1/2 * x^n-1/2 

四.实验任务4

 实验代码：

#include <stdio.h>

int is_prime(int num) {
if (num <= 1) return 0;
if (num == 2) return 1;
if (num % 2 == 0) return 0;

for (int i = 3; i * i <= num; i += 2) {
if (num % i == 0) return 0;
}
return 1;
}

int main() {
printf("100以内的孪生素数:\n");
for (int i = 2; i <= 98; i++) {
if (is_prime(i) && is_prime(i + 2)) {
printf("%d %d\n", i, i + 2);
}
}
return 0;
}

程序运行截图：

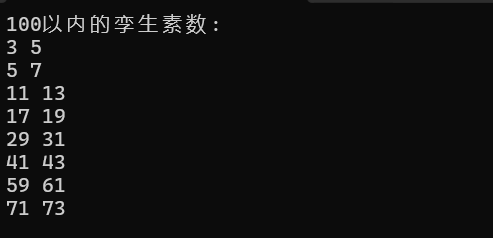
 五.实验任务5

实验代码：

#include<stdio.h>

int move_count = 0;

void hanoi(int n, char source, char target, char auxiliary) {
    if (n == 1) {
        move_count++;
        printf("%d:%c-->%c\n", n, source, target);
    }
    else {
        hanoi(n - 1, source, auxiliary, target);
        move_count++;
        printf("%d:%c-->%c\n", n, source, target);
        hanoi(n - 1, auxiliary, target, source);
    }
}

int main() {
    int n;

    while (1) {
        if (scanf_s("%d", &n) != 1) {
            break;
    }
        move_count = 0;
        hanoi(n, 'A', 'C', 'B');
        printf("\n一共移动了%d次。\n\n", move_count);
        while (getchar() != '\n');
    }
    return 0;
}

程序运行截图：

 六.实验任务6

迭代实验代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>

int func(int n, int m) {
    if (m > n) return 0;
    if (m == 0 || m == n) return 1;

    if (m > n - m) m = n - m;

    int result = 1;
    for (int i = 0; i < m; ++i) {
        result *= (n - i);
        result /= (i + 1);
    }
    return result;
}

int main() {
    int n, m;
    int ans;

    while (scanf("%d %d", &n, &m) != EOF) {
        ans = func(n, m);
        printf("n=%d,m=%d,ans=%d\n\n", n, m, ans);
    }
    return 0;
}

程序运行截图：

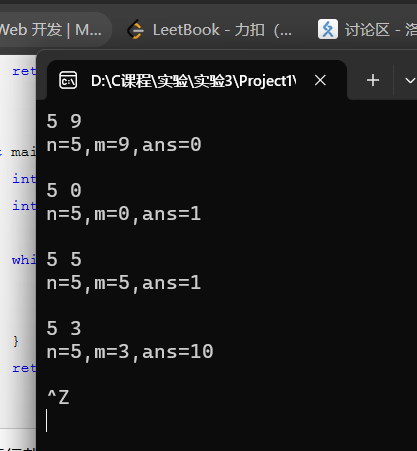
递归实验代码：

#define _CRT_SECURE_NO_WARNINGS

#include <stdio.h>

int func(int n, int m) {
    if (m > n) return 0;
    if (m == 0 || m == n) return 1;
    return func(n - 1, m - 1) + func(n - 1, m);
}

int main() {
    int n, m;
    int ans;

    while (scanf("%d %d", &n, &m) != EOF) {
        ans = func(n, m);
        printf("n=%d,m=%d,ans=%d\n\n", n, m, ans);
    }
    return 0;
}

程序运行截图：

 

 七.实验任务7

实验代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>

int gcd(int a, int b, int c) {
    int min;
    if (a < b) {
        if (a < c) {
            min = a;
        }
        else {
            min = c;
        }
    }
    else {
        if (b < c) {
            min = b;
        }
        else {
            min = c;
        }
    }

    for (int i = min; i >= 1; --i) {
        if (a % i == 0 && b % i == 0 && c % i == 0) {
            return i;
        }
    }
    return 1;
}

int main() {
    int a, b, c;
    int ans;

    while (scanf("%d%d%d", &a, &b, &c) != EOF) {
        ans = gcd(a, b, c);
        printf("最大公约数: %d\n\n", ans);
    }

    return 0;
}

程序运行截图：

 实验总结

经过上周的学习以及本次实验任务，对迭代以及递归的优劣有了一个较为清晰的认知。迭代的特点在易理解但是代码量比较多，递归的特点在于难想到难理解，但代码量很少。我认为更能体现对计算机学习的，人多思考机器多做事的特点！