《算法十》（动态规划）

动态规划：

　　使用动态规划：重叠子问题

　　最优值，最佳解

　　斐波那契数列问题：如果递归解决需要重复算很多次fib(5)

　　　　　　　　解决：使用一个数组把每次算过的存起来，下次再用直接调值

 

例题：

问题描述：

 

解答：

#include <iostream>
#include <iomanip> 
#include <math.h>
#include <string.h>
#define NUM 6 
using namespace std;

//递归 
bool isOk(int arr[], int i, int s){
	if( s==0 ){//如果要找的s是0，那么肯定OK 
		return true;
	}else if( i==0 ){//如果只剩下最后一个了，如果arr[0]==s的话OK，否则不成功 
		return arr[0]==s;
	}else if( arr[i]>s ){//如果当前的arr[i]的值超过要找的s，那么去掉它 
		return isOk(arr, i-1, s);
	}else{
		//2种选择：
		//第一种：选择当前值，那么相应s要去掉当前值，同时i-1 
		bool x = isOk(arr, i-1, s-arr[i]);
		//第二种：不选择当前值，那么直接i-1 
		bool y = isOk(arr, i-1, s);
		//2种选择任意一种成功就行 
		return (x||y);
	}
}

//非递归
bool feidigui(int arr[], int s){
	//构建辅助数组：
	//行等于arr数组的行，列代表s经过变化的可能取值(0~s:s+1个数) 
	bool arrTemp[NUM][s+1];
	 
	for(int i=0; i<NUM; i++){//第一列：s全部等于0，那么都是true 
		arrTemp[i][0] = true;
	}
	for(int i=0; i<s+1; i++){//第一行：只剩下一个值了，只有这个值和s相等才对，否则是false找不到 
		if( arr[0]==i )//这个值和s相等
			arrTemp[0][i] = true; 
		else//这个值和s不相等
			arrTemp[0][i] = false;
	}
	
	for(int i=1; i<NUM; i++){
		for(int j=1; j<s+1; j++){
			if(arr[i]>s){//如果当前的arr[i]的值超过要找的s，那么去掉它 
				arrTemp[i][j] = arrTemp[i-1][j];	
			}else{
				//选择当前值，那么相应j要去掉当前值，同时i-1 
				bool x = arrTemp[i-1][j-arr[i]];
				//不选择当前值，那么直接i-1  
				bool y = arrTemp[i-1][j];
				arrTemp[i][j] = (x or y);
			}
		}
	}
	return arrTemp[NUM-1][s];
} 

int main(void){
	int arr[] = {3, 34, 4, 12, 5, 2};
	
	if(isOk(arr, 5, 9)){
		cout << "true!" << endl;
	}else{
		cout << "false!" << endl;
	}
 	    
	if(feidigui(arr, 13)){
		cout << "true!" << endl;
	}else{
		cout << "false!" << endl;
	}	

	return 0;
} 

重点：

递归方法：找出递归出口+递归式

 

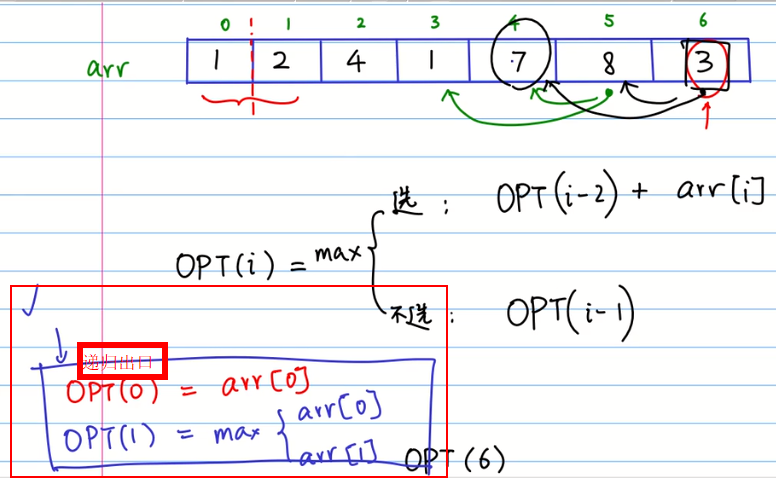
 非递归方法：构建一个二维数组，行存取0~5对应arr[i]，列存取从0~s个值(一共s+1个数)