《算法笔记》之算法初步

本篇主要内容：

基础算法：排序、散列、递归、贪心、二分以及其他高效技巧

一些算法题：八皇后、汉诺塔等

1.排序：

排序主要可以分为：选择排序、插入排序

选择排序：

　　主要介绍最为常用的简单选择排序

　　简单选择排序：基本思路是将一个序列分为1~n个单元，首先从这n个单元里选择出来最小的单元，将其与第一个位置的单元相交换，接着从2~n个单元里，找出最小单元，将其与第二个位置的单元相交换，依次进行下去......。这样在n趟操作之后就会形成一个从小到大的有序序列。

 

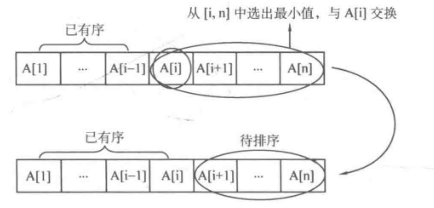
代码实现：一共进行n次操作，嵌套for循环，每次找出从i到n之中最小的数，然后与第i个位置数据进行交换

void SelectSort( int a[], int length )
{
    //对数组a排序,length是数组元素数量
    for( int i = 0; i < length; i++ ) {
        // 找到从i开始到最后一个元素中最小的元素,k存储最小元素的下标.
        int k = i;
        for( int j = i + 1; j < length; j++ ) {
            if( a[j] < a[k] ) { k = j; }
        }

        // 将最小的元素a[k] 和 开始的元素a[i] 交换数据.
        if( k != i ) {
            int temp;
            temp= a[k];
            a[k] = a[i];
            a[i] = temp;
        }
    }
}

插入排序：

　　主要介绍直接插入排序

　　直接插入排序：从2~n进行n-1次操作。假设这个时候是第i+1个数据，且前面1~i个数据均为有序数据，则将第i个数据插入到前面数据之中，因此可以采用for循环从2~n，内部嵌套上while循环，进行查找1~i之中第i+1个数据适合放在哪里。

void SelectSort(){
    for(int i=1;i<n;i++){
        int temp = A[i], j=i;
        while(j>0 && temp<A[j-1]){
            A[j] = A[j-1];
            j--;
        }
        A[j] = temp;
    }
} 

实例：

#include <iostream>
using namespace std;
int main(){

    int num[5] = {3, 7, 1, 8, 5};
    int i,j;
    int length = 5;

    for (i = 1; i < length; i++)
    {
        int temp = num[i];    
        j = i;    
        while ( j > 0 && num[j-1] > temp)
        {
            num[j] = num[j-1];
            j--;
        }
        num[j] = temp;    
    }
    
    for(int k=0;k<length;k++){//打印数组 
        cout<<num[k];
    }
    return 0;
}
结果：13578

选择排序之实例剖析：

#include<iostream>
using namespace std;

const int MAX_NUM = 100; 
//选择排序 
int main(){
    int a[MAX_NUM];
    int n;
    cin >> n;                       //共有n个整数待排序 
    for(int i = 0; i < n; ++i)      //输入n个整数 
        cin >> a[i];
    //下面对整个数组进行从小到大排序
    for(int i = 0; i<n-1 ;++i){     //每次循环将第i小的元素放好 
        int tmpMin = i;  //用来记录从第i个到第n-1个元素中,最小的那个元素的下标 
        for(int j=i; j<n;++j){
            if(a[j]<a[tmpMin])
                tmpMin = j;
        }
    //下面将第i小的元素放在第i个位置上,并将原来占着第i个位置的那个元素挪到后面
        int tmp = a[i];
        a[i] = a[tmpMin];
        a[tmpMin] = tmp; 
    }
    //下面两行将排序好的n个元素输出
    for(int i=0;i<n;++i)
        cout << a[i] << endl;
    return 0;
}

插入排序之实例剖析：

#include<iostream>
using namespace std;

//插入排序
void InsertionSort(int a[], int size)
{
    int i;          //有序区间的最后一个元素的位置,i+1就是无序区间最左边元素的位置
    for(i = 0; i < size-1; ++i){
        int tmp = a[i + 1];  //tmp是待插入到有序区间的元素,即无序区间最左边的元素
        int j = i;
        while(j >= 0 && tmp < a[j]){        //寻找插入的位置 
            a[j + 1] = a[j];                //比tmp大的元素都往后移动 
            --j;
        }
        a[j + 1] = tmp;
    }
}

//输出二维数组,rows是行数
void PrintArray(int a[][5], int rows)
{
    for(int i = 0; i < rows; ++i){
        for(int j = 0; j < 5; ++j)
            cout << a[i][j] << " ";
        cout << endl;
    }
} 


//主函数 
int main(){
    int b[5] = {50, 30, 20, 10, 40};
    int a2d[3][5] = {{5, 3, 2, 1, 4},{10, 20, 50, 40, 30},{100, 120, 50, 140, 30}};
    InsertionSort(b, 5);
    for(int i = 0; i < 5; ++i)
        cout << b[i] << " ";
    cout << endl;
    for(int i = 0; i < 3; ++i)      //将 a2d每一行均排序 
        InsertionSort(a2d[i], 5);
    PrintArray(a2d, 3);
    return 0;
}

 

2.散列

　　哈希表(也可以叫做散列表)，是根据  键（Key）而直接访问在内存存储位置的数据结构，也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做哈希表。

　　哈希函数构造：

　　如果字符串S由A~Z组成：

　　

 

 　　如果字符串S由A~Z/a~z组成：

　　

 

 3.全排列问题（递归）：

//全排列：视频参考哔哩哔哩：正月点灯笼 
#include <stdio.h>

void swap(int A[], int i, int j){//用于交换数组的2个值 
    int temp = A[i];
    A[i] = A[j];
    A[j] = temp;
}

void printArray(int A[], int n){//用于打印数组 
    int i;
    for(i=0;i<n;i++){
        printf("%d ", A[i]);
    }
    printf("\n");
}

void perm(int A[], int p, int q){//全排列递归函数；p,q代表对数组A全排列的起始和结束 
    if(p == q){//递归结束条件 
        printArray(A, q+1);
    }
    else{
        int i;
        for(i=p; i<=q; i++){
            swap(A, p, i);
            perm(A, p+1, q);
            swap(A, p, i);
        }
    }    
} 

int main(){
    int A[4] = {1, 2, 3, 4};
    perm(A, 0, 3);
    return 0;
}

4.N皇后问题：

//参考视频：小甲鱼算法视频（八皇后问题） 
#include <stdio.h>

//count代表：共有多少种解决方法 
int count = 0; 
//row：表示起始行
//n：表示列数 
//(*chess)[8]：指向棋盘的行指针 

int noDanger(int row, int j, int (*chess)[8]){//判断可不可以放棋子：为1，可以；为0，不可以； 
    int i, k, flag1 = 0, flag2 = 0, flag3 = 0, flag4 = 0, flag5 = 0;
    //判断列的方向 
    for(i=0; i<8; i++){
        if(*(*(chess+i)+j)!=0){
            flag1 = 1;
            break;
        }
    }
    //判断左上方
    for( i=row, k=j; i>=0 && k>=0; i--, k--){
        if(*(*(chess+i)+k)!=0){
            flag2 = 1;
            break;
        }
    }
    //判断右下方 
    for( i=row, k=j; i<8 && k<8; i++, k++){
        if(*(*(chess+i)+k)!=0){
            flag3 = 1;
            break;
        }
    }
    //判断右上方 
    for( i=row, k=j; i>=0 && k<8; i--, k++){
        if(*(*(chess+i)+k)!=0){
            flag4 = 1;
            break;
        }
    }
    //判断左下方 
    for( i=row, k=j; i<8 && k>=0; i++, k--){
        if(*(*(chess+i)+k)!=0){
            flag5 = 1;
            break;
        }
    }
    if(flag1 || flag2 || flag3 || flag4 || flag5){
        return 0;//0：代表不可以摆放棋子 
    }else{
        return 1;//1：代表该摆放位置正确，可以摆放棋子 
    }
}

//EightQueen:主要的递归函数 
//(*chess)[8]：指向棋盘的行指针
//row指从哪一行开始
//n代表总列数 
void EightQueen(int row, int n, int (*chess)[8]){
    int chess2[8][8], i, j;
    for(i=0; i<8; i++){//复制chess数组 
        for(j=0; j<8; j++){
            chess2[i][j] = chess[i][j];
        }
    }
    if(row == 8){//结束条件：当到达最后一行的时候 
        printf("第%d种\n", count+1); 
         for(i=0; i<8; i++){//打印出来解决方法 
            for(j=0; j<8; j++){
            printf("%d ", *(*(chess2+i)+j));
        }
        printf("\n");
      }
      printf("\n");
      count++; //解决方法+1 
    }
    else{//递归体 
        for( j=0; j<n; j++){
            if(noDanger(row, j, chess)){//noDanger：为1代表可以摆放棋子；为0代表不可以摆放棋子 
                for( i=0; i<8; i++){//首先把这一行所有棋子先全置为0 
                    *(*(chess2+row)+i) = 0;
                }
                *(*(chess2+row)+j) = 1;//将noDanger为1的第row行第j列置为1 
                EightQueen(row+1, n, chess2);//递归进行下一行的探测 
            }
        } 
    } 
}

int main(){
    int chess[8][8], i, j;
    for(i=0; i<8; i++){
        for(j=0; j<8; j++){
            chess[i][j] = 0;
        }
    }
    EightQueen(0, 8, chess);
    printf("\n一共有%d种解决方法", count);
    return 0;
} 

5.汉诺塔问题：

//参考视频：正月点灯笼(汉诺塔)
#include <stdio.h>

int count=0;

//hanoi函数：hanoi(int n, char A, char B, char C)理解（将n个盘子从A经过B移动到C） 
void hanoi(int n, char A, char B, char C){
    if(n==1){
        printf("%c-->%c\n", A, C);
    }else{
        hanoi(n-1, A, C, B);
        printf("%c-->%c\n", A, C);
        hanoi(n-1, B, A, C);
    }
    count++;
}

int main(){
    hanoi(6, 'A', 'B', 'C');
    printf("一共移动%d次\n", count);
    return 0;
} 

6.归并排序：

//参考视频：正月点灯笼
#include <stdio.h>

void merge(int arr[], int L, int M, int R){//有序数组合并合并 
    int L_size = M-L;
    int R_size = R-M+1;
    int left[L_size];//有序数组left：0~4 
    int right[R_size];//有序数组right：4~7 
    int i, j, k;
    for(i=0; i<=R; i++){//为left和right数组赋值 
        if(i<M){
            left[i] = arr[i];    
        }
        else{
            right[i-M] = arr[i];
        }
    }
    i = 0, j = 0, k = L;//i为left数组起点；j为right数组起点；k为arr数组起点； 
    while(i<L_size && j<R_size){//比较大小 
        if(left[i] > right[j]){
            arr[k] = right[j];
            k++;
            j++;
        }else{
            arr[k] = left[i];
            k++;
            i++;
        }
    }
    while(i<L_size){//如果left数组有剩余 
        arr[k] = left[i];
        k++;
        i++;
    }
    while(j<R_size){//如果right数组有剩余 
        arr[k] = right[j];
        k++;
        j++;
    }
} 

void mergesort(int arr[], int L, int R){//归并排序 
    if( L==R ){//递归终止条件 
        return ;
    }else{//递归体 
        int M = (L+R)/2;//M=3=(0+7)/2； 
        mergesort(arr, L, M);
        mergesort(arr, M+1, R);
        merge(arr, L, M+1, R);//如果L=0,R=7；那么此时merge合并时候的M应该为4=(0+7)/2+1； 
    }
} 

int main(){
    //arr数组中0~4有序，4~7有序
    //归并排序：将2个有序数组合并成为一个有序数组 
    
    //测试merge函数 
    /*int arr[8] = {2, 8, 9, 10, 4, 5, 6, 7};
    int L = 0;
    int M = 4;
    int R = 7;
    printf("排序前:");
    for(int i=0; i<8; i++){
        printf("%d ",arr[i]);
    }
    printf("\n"); 
    merge(arr, L, M, R);
    printf("排序后:");
    for(int i=0; i<8; i++){
        printf("%d ",arr[i]);
    }*/
    
    //测试mergesort函数 
    int arr[8] = {2, 8, 9, 10, 4, 5, 6, 7};
    int L = 0;
    int R = 7;
    mergesort(arr, L, R);
    for(int i=0; i<8; i++){
        printf("%d ",arr[i]);
    }
    return 0;
} 

7.几种经典排序实现：

冒泡排序：

//参考视频：正月点灯笼
#include <stdio.h>

//一次冒泡 
void bubble(int arr[], int n){
    int i, temp;
    for(i=0; i<n-1; i++){
        if(arr[i]>arr[i+1]){
            temp = arr[i];
            arr[i] = arr[i+1];
            arr[i+1] = temp; 
        }
    }
} 

//冒泡排序 
void bubblesort(int arr[], int n){
    for(int i=n; i>=1; i--){
        bubble(arr, i);
    }
} 
 
//测试 
int main(){
    int arr[]={2,1,5,4,3,6};
    bubblesort(arr, 6);
    for(int i=0; i<6; i++){
        printf("%d ",arr[i]);
    }
    return 0;
}

选择排序：

//参考视频：正月点灯笼
#include <stdio.h>

//找到最大值的下标 
int findMaxPos(int arr[], int n){
    int max = arr[0];//max
    int pos = 0;//max的下标 
    int i;
    for(i=0; i<n; i++){
        if(arr[i]>max){
            max = arr[i];
            pos = i; 
        }
    }
    return pos;
} 

//选择排序
void selectsort(int arr[], int n){
    while(n>1){
        int pos = findMaxPos(arr, n);
        int temp = arr[pos];
        arr[pos] = arr[n-1];
        arr[n-1] = temp; 
        n--;
    }
} 
 
//测试 
int main(){
    int arr[]={2,1,5,4,3,6};
    selectsort(arr, 6);
    for(int i=0; i<6; i++){
        printf("%d ",arr[i]);
    }
    return 0;
} 

8.KMP算法：

//参考视频：正月点灯笼
#include <stdio.h>

//求next数组（s代表字符串，next代表next数组，n代表长度）
void next_table(char s[], int next[], int n){
    next[0] = 0;
    int len = 0;
    int i = 1;;
    while(i<n){
        if(s[i] == s[len]){
            len++;
            next[i] = len;
            i++;
        }
        else{
            if(len > 0){
                len = next[len-1];
            }
            else{
                next[i] = len;
                i++;
            }
        }
    }
} 

int main(){
    char s[] = "ABABCABAA";
    int next[9];
    int n = 9;
    next_table(s, next, n);
    for(int i=0; i<n; i++){
        printf("%d ", next[i]);
    }
    return 0;
} 

9.动态规划：

理论讲解推荐：https://www.bilibili.com/video/av16544031（强👍）