[一天一题]简单的几何？

数形结合百般好！！！

题目

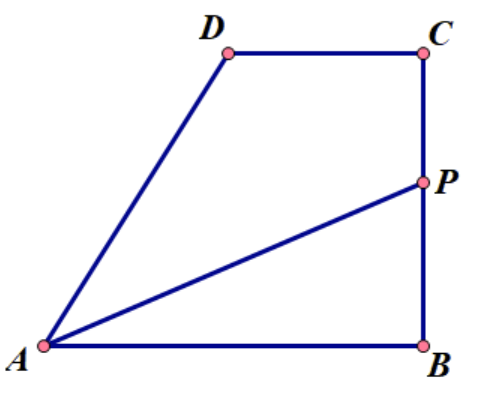
如图一，在\(四边形_{ABCD}\) 中，\(AB \parallel CD,AB \perp BC\),\(动点P\) 从 \(点B\) 出发，沿着\(B\rightarrow C\rightarrow D\rightarrow A\) 方向运动，到\(点A\) 停止，设\(点P\)运动路程为\(x\)，\(\triangle ABP\) 的面积为\(y\)，如果\(y\) 与\(x\) 的函数图像如图二所示，则\(AB\)长为多少?
图一：

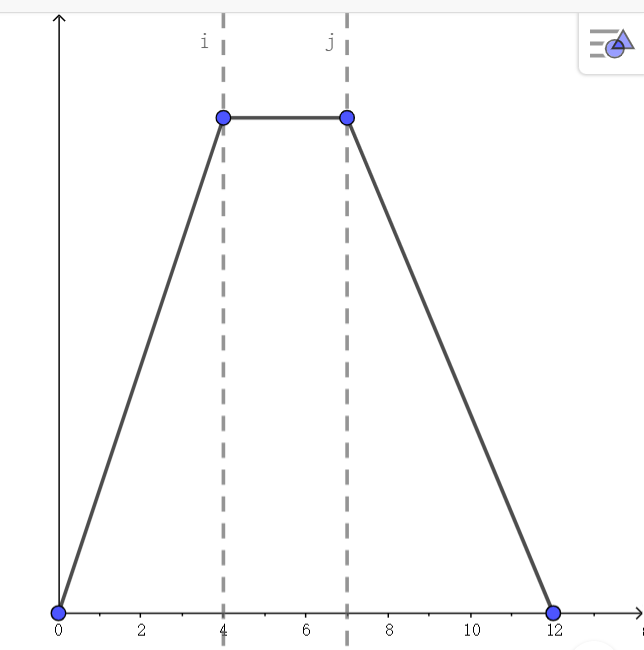
图二：

分析

观察图像，因为当\(动点P\) 在\(DC\) 段时，\(S_{\triangle ABP}\) 不变，易得\(BC = 4\)，从而\(DC=3,AD=5\).
现在，过\(点D\) 作\(DE \perp AB\) 于\(点E\).

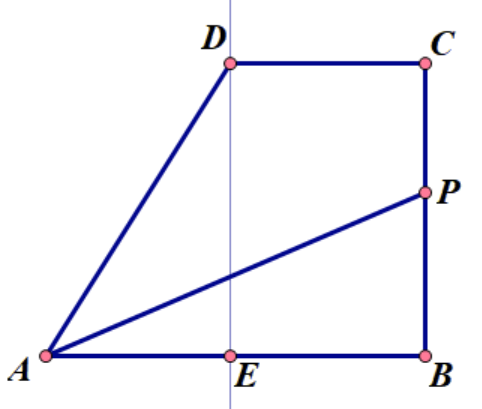
可得\(Rt\triangle ADE,DE=BC=4,BE=CD=3\).
在\(Rt\triangle ADE\) 中，由勾股定理得:

\[\begin{equation*} \begin{split} AE & = \sqrt{AD^{2} - DE^{2}} \\ & = \sqrt{5^{2}-4^{2}} \\ & = \sqrt{9} \\ & = 3 \end{split} \end{equation*} \]

则\(AB = AE + BE = 3+3 = 6\).

答案

\(6\).