一种比较简洁的线段树写法
线段树是一种高效的数据结构,旨在快速的处理区间的修改和查询问题,单次操作复杂度为O(logn)
但我们今天的重点并非讲解线段树的诞生及其原理,而是总结一下线段树代码以及基础的用法
只有原理是写不出代码的,那是纯纯的发明创造
先贴板子,可能不是最先进的,但我相信我的版本一定是比较简洁易懂的
(简洁 != 短,比起无脑压行,我相信适当的多写几行是有助于理解的。
本人喜欢将数据结构封装起来,所以用到了一点其他的知识,但是很简单)
struct SegTree {
#define lc u << 1
#define rc u << 1 | 1
typedef struct node {
int l, r;
i64 val, tag;
} node;
std::vector<i64> a;
std::vector<node> tree;
SegTree (int size) {
a.resize(size + 10);
tree.resize(4 * size + 10);
}
void push_up (int u) {
/* tree[u].val = tree[lc].val ?? tree[rc].val */
}
void push_down (int u) {
if (tree[u].tag) {
// Left:
// Right:
// Final
tree[u].tag = 0;
}
}
void build (int u, int l, int r) {
tree[u].l = l;
tree[u].r = r;
tree[u].tag = 0;
if (l == r) {
tree[u].val = a[l];
return;
}
int mid = tree[u].l + tree[u].r >> 1;
build(lc, l, mid);
build(rc, mid + 1, r);
push_up(u);
}
void update (int u, int x, int y, i64 k) {
if (x <= tree[u].l && tree[u].r <= y) {
// tree[u].val = ??
// tree[u].tag = ??
return;
}
push_down(u);
int mid = tree[u].l + tree[u].r >> 1;
if (x <= mid) update(lc, x, y, k);
if (y > mid) update(rc, x, y, k);
push_up(u);
}
i64 query (int u, int x, int y) {
if (x <= tree[u].l && tree[u].r <= y) {
return tree[u].val;
}
push_down(u);
int mid = tree[u].l + tree[u].r >> 1;
i64 ans = 0;
if (x <= mid) /* ans <-- query(lc, x, y); */
if (y > mid) /* ans <-- query(rc, x, y); */
return ans;
}
};
线段树入门第一步:结构体和宏定义
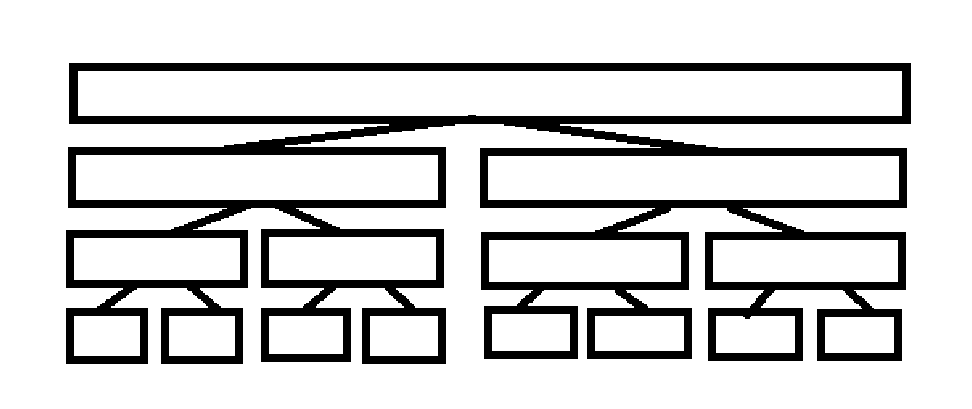
线段树是一棵满二叉树,因此,如果当前节点为u,那么我们就可以用u * 2和u * 2 + 1来访问他的两个子节点
因此,我们加入这两句宏定义:
#define lc u << 1
#define rc u << 1 | 1
这里的 << 和 | 是位运算符,其中u<< 1就是u * 2,u << 1 | 1就是u * 2 + 1
我们用lc代表左子节点,rc代表右子节点
接下来,我们用结构体来定义线段树的节点
typedef struct node {
int l, r;
i64 val, tag;
} node;
l和r表示当前节点表示的区间,val是你要求的东西(比如区间和、区间最值),tag是懒标记
别问为什么,照着这么写就行了,用结构体封装,后续会方便很多
线段树入门第二步:构造函数
如果想要在使用线段树就像使用STL容器那么自然,那么我们就手动封装起来整个线段树,让他“成为STL容器”
struct SegTree {
std::vector<i64> a;
std::vector<node> tree;
SegTree (int size) {
a.resize(size + 10);
tree.resize(4 * size + 10);
}
};
我们在内部定义数组a和线段树数组tree,数组a就是你需要操作的目标序列
线段树数组用先前的node结构体,线段树要开原数组a的四倍空间
我们使用构造函数,重新设置数组和线段树数组的空间,这样的话,在主函数中我们可以这么写:
int main () {
int n;
std::cin >> n;
SegTree T(n);
for (int i = 1; i <= n; i++) {
std::cin >> T.a[i];
}
T.build(1, 1, n);
return 0;
}
这里的SegTree T(n);就是开了一个针对长度为n的序列的线段树
使用for循环输入T.a数组中的每一位,再调用T.build()函数去建立线段树
而接下来,我们就要进行线段树的建树操作
线段树入门第三步:建立线段树
建立线段树的时候,我们需要通过递归的方式来实现
当建立代表[l, r]这个区间的节点时
接下来就需要去建立代表[l, mid]和[mid + 1, r]的两个节点了
这里的mid = l + r >> 1(线段树为了减少代码量,一些地方采用位运算,这里的 >> 1 就是 ÷ 2 的意思)
当l == r的时候,就代表着到了叶子节点,此时没有子节点,要赋值并return
再层层return的时候,我们要执行push_up操作进行向上传递,更新父节点的值
push_up()函数同样是由自己定义的,去实现自己需要的操作
比如说,我们要求区间和,那我们的push_up()函数就是
tree[u].val = tree[lc].val + tree[rc].val
如果是区间最值,那么
tree[u].val = std::max(tree[lc].val, tree[rc].val)
也可以是区间gcd
tree[u].val = std::__gcd(tree[lc].val, tree[rc].val)
代码如下:
void push_up (int u) {
/* tree[u].val = tree[lc].val ?? tree[rc].val */
}
void build (int u, int l, int r) {
tree[u].l = l;
tree[u].r = r;
tree[u].tag = 0;
if (l == r) {
tree[u].val = a[l];
return;
}
int mid = tree[u].l + tree[u].r >> 1;
build(lc, l, mid);
build(rc, mid + 1, r);
push_up(u);
}
线段树入门第四步:query函数
给定了需要查询的区间[x, y],现在执行查询操作,从[1, n]区间开始层层向下查找
假设当前查到了代表[l, r]区间的节点,那么我们进行判断
- 如果区间[l, r]被完全包含在[x, y]查询的区间内,那么return
- 否则,我们要继续向下查找
那么向下查找的时候,是向左,还是向右呢?
我们此时需要再加一个判断,定义mid = tree[u].l + tree[u].r >> 1
- 如果x <= mid,那么需要向左子节点查询
- 如果y > mid,那么需要向右子节点查询
我们需要定义一个ans,然后在return过程中层层更新,代码如下:
(这里的push_down()操作我们稍后会讲)
i64 query (int u, int x, int y) {
if (x <= tree[u].l && tree[u].r <= y) {
return tree[u].val;
}
push_down(u);
int mid = tree[u].l + tree[u].r >> 1;
i64 ans = 0;
if (x <= mid) /* ans <-- query(lc, x, y); */
if (y > mid) /* ans <-- query(rc, x, y); */
return ans;
}
线段树入门第五步:update和push_down函数
我们到了线段树最重要的部分,这部分是线段树能够始终在O(logn)复杂度完成区间修改的核心
懒标记
试想一下,如果我们给定了一个区间[x, y]需要进行修改/更新
那当我们找到了被[x, y]完全包含的区间[l, r],我们还要不要向下继续更新?
如果不向下更新,那么我们后续查询到下面的节点时,获取的答案就是错误的
但如果我们更新了,更新操作的复杂度就不再是O(logn)了,会退化成O(n),失去了意义
此时我们引入了懒标记
懒标记:顾名思义,懒
如果我们更新到某个被完全包含的区间,不是向下更新,而是打上一个标记,告诉程序:我这里有待更新,会怎么样呢?
当程序下次查询到下面的节点时,因为被告知有待更新,所以会对下面进行更新操作,这样是不是就保证了答案的正确性?
所以,懒标记的作用就是,告诉我们此处需要更新的值,至于如何更新,就看我们的操作了
push_down操作分为三步:
- 修改左子节点的val值和tag值
- 修改右子节点的val值和tag值
- 将当前节点的tag值置为0或者初始值
向下更新完之后,记得向上也要更新,代码如下:
void push_down (int u) {
if (tree[u].tag) {
// Left:
// Right:
// Final
tree[u].tag = 0;
}
}
void update (int u, int x, int y, i64 k) {
if (x <= tree[u].l && tree[u].r <= y) {
// tree[u].val = ??
// tree[u].tag = ??
return;
}
push_down(u);
int mid = tree[u].l + tree[u].r >> 1;
if (x <= mid) update(lc, x, y, k);
if (y > mid) update(rc, x, y, k);
push_up(u);
}
现在给出一个区间和线段树的模板,可通过洛谷P3372【模板】线段树 1
下面的代码中,重点的地方会通过注释的方法讲解
struct SegTree {
#define lc u << 1
#define rc u << 1 | 1
typedef struct node {
int l, r;
i64 sum, tag;
} node;
std::vector<i64> a;
std::vector<node> tree;
SegTree (int n) {
a.resize(n + 10);
tree.resize(4 * n + 10);
}
void push_up (int u) {
// 因为我们求的是区间和,所以在向上更新时,大区间的区间和 = 两个小区间的区间和相加
// 也就是父节点区间和 = 左子节点区间和 + 右子节点区间和
tree[u].sum = tree[lc].sum + tree[rc].sum;
}
void push_down (int u) {
// push_down函数是很重要的一部分,注意这里的写法
// 当懒标记存在的时候,我们进行下传的操作,如果不存在就不用了
if (tree[u].tag) {
// 修改左子节点的情况
// 由于我们是区间和线段树,我们这里的更新操作是“区间内每个数字 + k”
// 因此我们的tree[lc].sum += 区间长度 * tree[u].tag
// 区间长度 = (tree[lc].r - tree[lc].l + 1)
// tree[u].tag是经过一层层传下来的值,意思是,当前区间每个数字需要加上tree[u].tag
tree[lc].tag += tree[u].tag;
tree[lc].sum += (tree[lc].r - tree[lc].l + 1) * tree[u].tag;
// 右子节点同理,不再赘述
tree[rc].tag += tree[u].tag;
tree[rc].sum += (tree[rc].r - tree[rc].l + 1) * tree[u].tag;
// 更新完了,就让当前节点的tag值置为0,意思是下次不用再下传啦
tree[u].tag = 0;
}
}
void build (int u, int l, int r) {
tree[u].l = l;
tree[u].r = r;
tree[u].tag = 0;
if (l == r) {
tree[u].sum = a[l];
return;
}
int mid = tree[u].l + tree[u].r >> 1;
build(lc, l, mid);
build(rc, mid + 1, r);
push_up(u);
}
void update (int u, int x, int y, i64 num) {
if (x <= tree[u].l && tree[u].r <= y) {
// 当更新操作更新到“被完全包含的区间”时,就不要继续向下走了
// 只更新当前节点的区间和,在这里打上标记
// 在后续push_down操作时,以此标记向下传递
// 注意是 += 而不是 = !!!
// 因为我们的tag值可能不是0,如果是直接赋值,相当于无视了先前的“修改申请”
tree[u].sum += (tree[u].r - tree[u].l + 1) * num;
tree[u].tag += num;
return;
}
push_down(u);
int mid = tree[u].l + tree[u].r >> 1;
if (x <= mid) update(lc, x, y, num);
if (y > mid) update(rc, x, y, num);
push_up(u);
}
i64 query (int u, int x, int y) {
if (x <= tree[u].l && tree[u].r <= y) {
return tree[u].sum;
}
push_down(u);
int mid = tree[u].l + tree[u].r >> 1;
i64 ans = 0;
if (x <= mid) ans += query(lc, x, y);
if (y > mid) ans += query(rc, x, y);
return ans;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号