容斥原理的应用

CF偶遇容斥原理，拼尽全力无法战胜
于是补了一下相关题目，现做出如下总结

容斥原理
为了不重不漏的计数，使重叠部分不被重复计算，所研究出的计数方法，为容斥原理
这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来
然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复

Educational Codeforces Round 181 (Rated for Div. 2) C. Count Good Numbers
https://codeforces.com/contest/2125/problem/C
给定l和r，要求计算出 [l, r] 区间内有多少数字，在质因数分解后，质因子全都不是个位数
说白了，意思就是计算出 [l, r] 内有多少数字不是 {2, 3, 5, 7} 的倍数

这道题考察容斥原理的应用，会了就一眼秒，不会就坐牢
我们用Venn图来表示：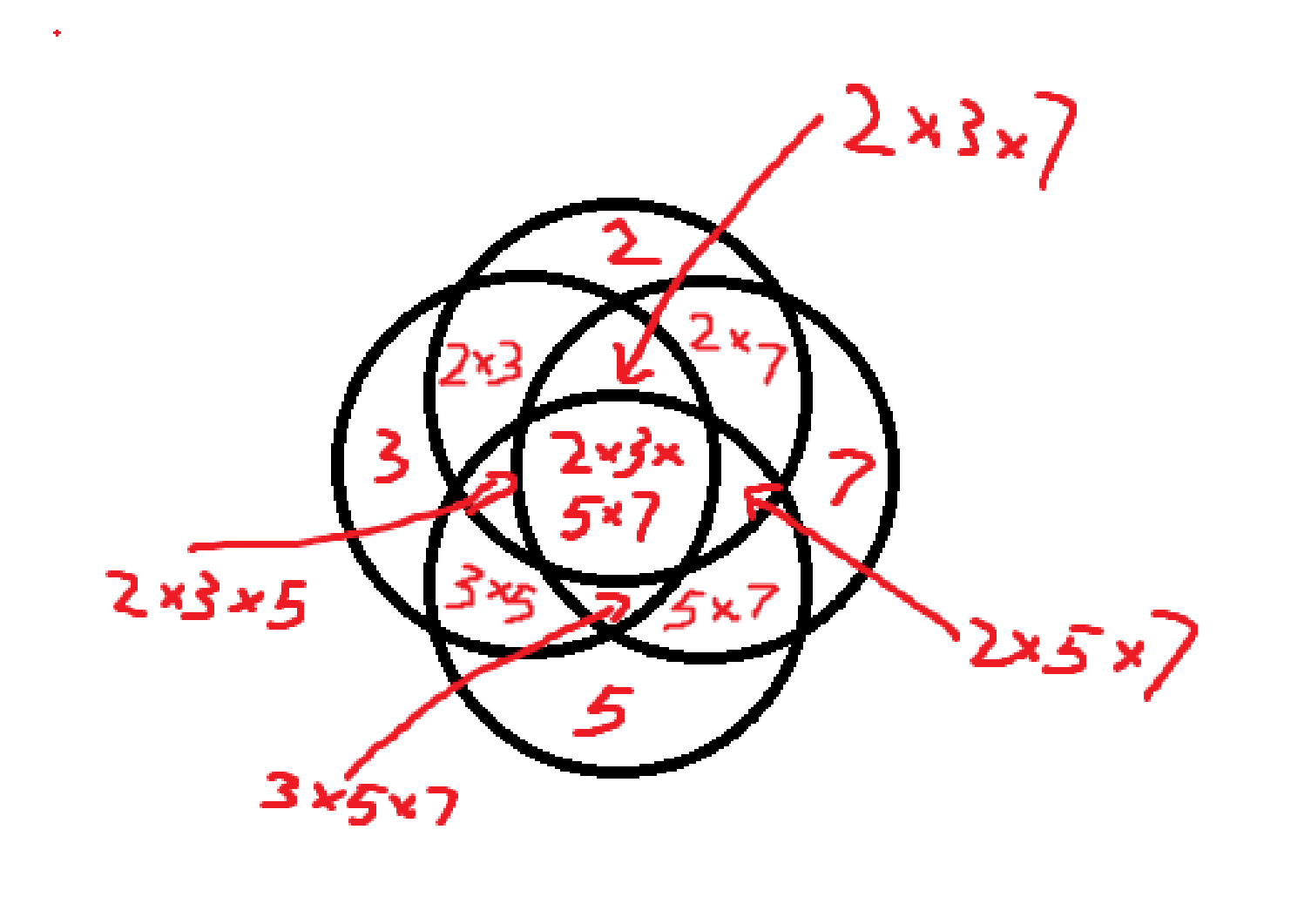

这个图太复杂了，我们先从小一点的开始，比如2和3的所有倍数

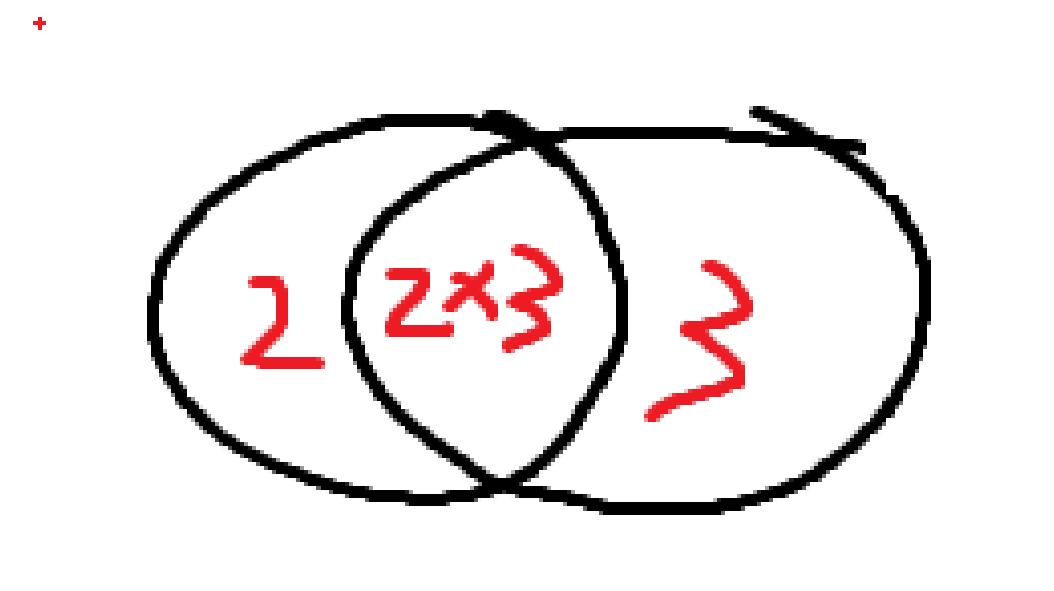
我们统计所有2的倍数的数量，再加上3的倍数的数量，那么2和3的共同倍数就会被统计两遍
因此，我们需要再减去2和3的共同倍数的数量，也就是减去6的倍数的数量

我们现在更进一步，统计2 3 5的倍数的数量

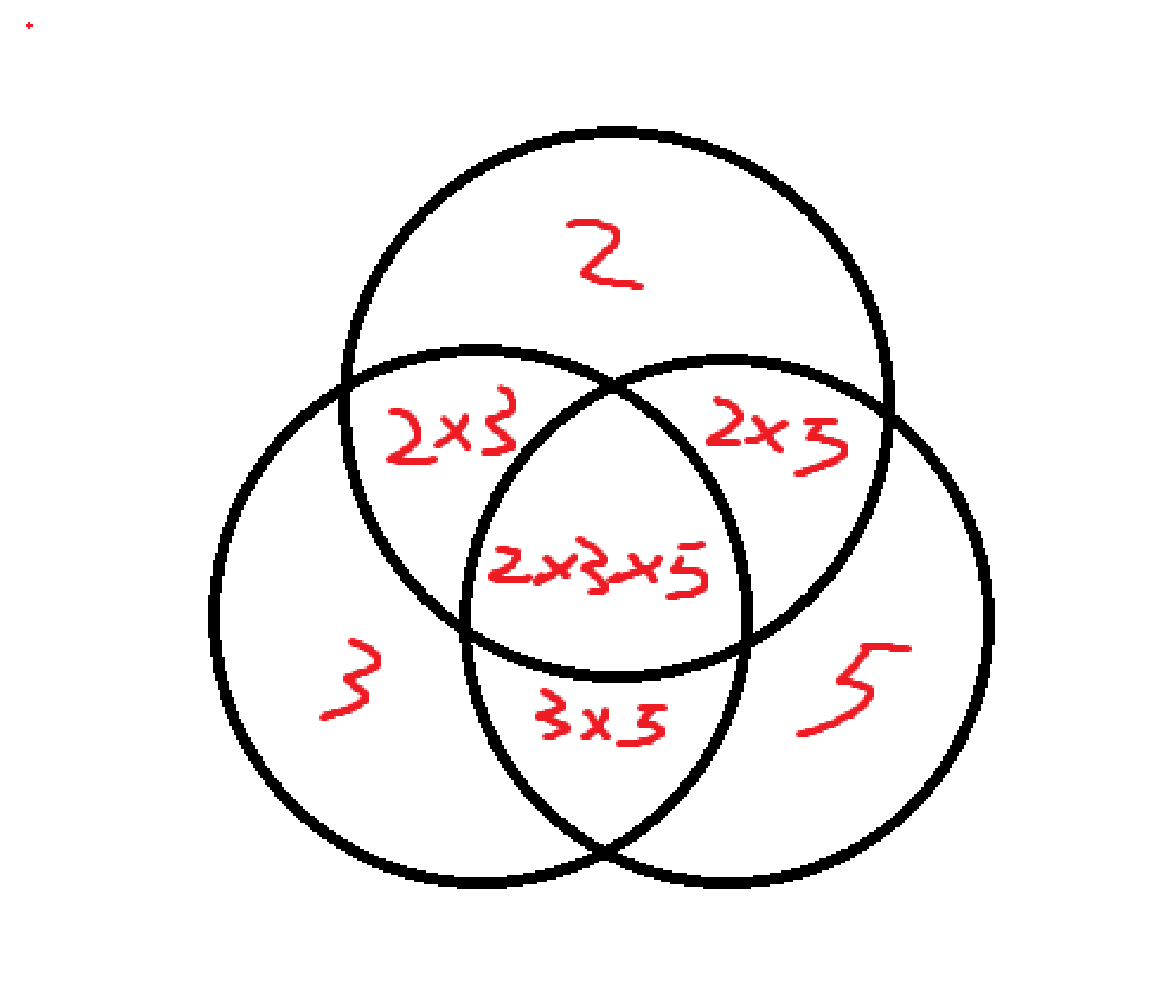
此时，我们先分别统计2、3、5的倍数的数量再相加，我们可以发现
2和3的共同倍数被统计两次，3和5的共同倍数被统计两次，2和5的共同倍数被统计两次
而2和3和5的共同倍数总共被统计了三次
因此，我们需要减去2和3的共同倍数，3和5的共同倍数，2和5的共同倍数
但是我们可以发现，这么一减，2和3和5的共同倍数被减去了三次，减没了
因此，我们需要再加上2和3和5的共同倍数的数量，也就是2 * 3 * 5 == 30的倍数的数量

也就是说，如果想要不重不漏的统计2 3 5 7的所有倍数，我们需要进行如下操作：（设cal(x)为x的倍数数量）

1. ans += cal(2) + cal(3) + cal(5) + cal(7);
2. ans -= cal(2×3) - cal(2×5) - cal(2×7) - cal(3×5) - cal(3×7) - cal(5×7);
3. ans += cal(2×3×5) + cal(3×5×7) + cal(2×3×7) + cal(2×5×7);
4. ans -= cal(2×3×5×7);

计算区间内XX的倍数有多少个的思路类似于前缀和
比如[l, r]区间内2的倍数个数 == [0, r]内2的倍数个数 - [0, l - 1]内2的倍数个数
代码如下：

/*====================My_Solution====================//

    要判断有多少个合数，分解为质数相乘的格式后，每个质因子都是> 10的
    哪怕是O(1)的复杂度判断也不可，因为区间范围1e18

    首先，2 3 5 7 的倍数全部pass
    最少也得是11 13 17这些数字的倍数
    经暴力计算证明，确实如此

    也就是说，我们需要判断，[l, r]区间内，有多少数字不是2 3 5 7的倍数
    如果线性筛，也不行，毕竟1e18，我们需要考虑其他方法

//====================My_Solution====================*/ 

void solve () {
    i64 l, r;
    std::cin >> l >> r;

    auto cal = [&] (i64 l, i64 r, i64 x) {
        return (r / x - (l - 1) / x);
    };

    std::vector<i64> p1 = {2, 3, 5, 7};
    std::vector<i64> p2 = {6, 10, 14, 15, 21, 35};
    std::vector<i64> p3 = {30, 42, 70, 105};

    i64 res = 0, ans = r - l + 1;
    for (auto it : p1) {
        res += cal(l, r, it);
    }
    for (auto it : p2) {
        res -= cal(l, r, it);
    }
    for (auto it : p3) {
        res += cal(l, r, it);
    }
    res -= cal(l, r, 210);

    std::cout << ans - res << '\n';
}

Codeforces Round 725 (Div. 3) F. Interesting Function
https://codeforces.com/contest/1538/problem/F
给定区间[l, r]，每次+1，进行r - l次操作后会从l变成r
要求求出在这个过程中，每次加法操作所改变的数字个数之和
例：

1. 如果是 l=909 进行加 1，变成910，有2个数被改变
2. 如果在 l=9 进行加 1，结果将是10，有2个数被改变
3. 如果向 l=489999 进行加一，结果是490000，有5个数被改变

既然会了容斥原理了，这道题就很简单了
我们可以发现，如果某个数字有连续个后缀9
那么这次操作会在原先的r - l次上，额外贡献一次
那么答案就很简单了，我们只需要统计，[l, r]范围内
10、100、1000、10000……10000000的个数即可
代码如下

/*====================My_Solution====================//

    如果一个数字有x个连续后缀9，那么答案额外+x
    也就是说，要统计l到r范围内有多少个以9为后缀的数字
    说白了，就是r / 10，r / 100， r / 1000， r / 10000这样

//====================My_Solution====================*/ 

void solve () {
    i64 l, r;
    std::cin >> l >> r;

    auto check = [&] (int x) {
        return (r / x) - (l / x);
    };

    std::vector<i64> a(10);
    a[1] = check(10);
    a[2] = check(100);
    a[3] = check(1000);
    a[4] = check(10000);
    a[5] = check(100000);
    a[6] = check(1000000);
    a[7] = check(10000000);
    a[8] = check(100000000);
    a[9] = check(1000000000);

    i64 ans = r - l;
    for (int i = 1; i <= 9; i++) {
        ans += a[i];
    }
    std::cout << ans << '\n';
}