2025.5.15
刷题日记
今天是板刷1600的第二天
过了4道题,其中两道1700,虽然很坐牢,但最终理解思路并AC的那一下真的好爽
虽然最终还是有一道题拼尽全力无法战胜吧,但真的能感觉到自己在一点点进步
话说刚才舍友问我一道1500的题,我读完题竟然直接给秒了,然后点开官方题解一看发现我的竟然还更简单一点,我感觉很不可思议
今天写的第一道题是Round_1018的C题,一场Div.1 + Div.2
https://codeforces.com/problemset/problem/2096/C
上来就是一个二维的dp,有种被缴械的无力感
这道题给了一个矩阵,要求使用以下两种操作,使得矩阵中不能出现相邻且大小相等的数字
1.选择a[i], 让矩阵第i行都+1, 同时cost += a[i]
2.选择b[j], 让矩阵第j列都+1, 同时cost += b[j]
题目要求需要最小化cost并输出
这道题刚看到的时候真的毫无思路
瞪了半天最终放弃了,决定去读题解
经过了两小时,读了三篇题解看了一个佬的讲解视频后,终于幡然醒悟
核心: 行和列的操作是互不影响的!
当你选中第i行并进行+1操作的时候,那么其中的每一列之间,都没发生相对的变化
比如第i行是 1 1 2 3 6 5,当你+1时,变成了2 2 3 4 7 6
那么显然,之前1 1是不合要求的,变成2 2后仍然不合要求
同时我们注意到贪心是写不出来的,所以要考虑dp了
(不过这个dp的状态我还是没想到,不得不学习题解)
设f[i][0]表示前i行且第i行未进行操作的最小cost
f[i][1]表示前i行且第i行进行操作的最小cost
那么对于本题则有:
- f[i][0] = std::min(f[i - 1][0], f[i - 1][1])
- f[i][1] = std::min(f[i - 1][0] + a[i], f[i - 1][1] + a[i])
这道题所具有的特殊情况为:
- 如果该行比上一行多1,那么上一行不能动
- 如果该行比上一行少1,那么该行不能动
我们可以开一个二维的dp数组
点击查看代码
std::vector f1(n + 1, std::vector<ll>(2, INF));
f1[1][0] = 0, f1[1][1] = a[1];
ll ans = 0;
for (int i = 2; i <= n; i++) {
int x = 1, y = 1, z = 1;
for (int j = 1; j <= n; j++) {
ll d = h[i][j] - h[i - 1][j];
if (d == 1) x = 0;
if (d == 0) y = 0;
if (d == -1) z = 0;
}
// 当不存在“第i-1行比第i行少1”的情况时
if (x) f1[i][0] = std::min(f1[i][0], f1[i - 1][1]);
// 当不存在“第i-1行和第i行相同”的情况时
if (y) f1[i][0] = std::min(f1[i][0], f1[i - 1][0]);
if (y) f1[i][1] = std::min(f1[i][1], f1[i - 1][1] + a[i]);
// 当不存在“第i-1行比第i行多1”的情况时
if (z) f1[i][1] = std::min(f1[i][1], f1[i - 1][0] + a[i]);
}
ans += std::min(f1[n][1], f1[n][0]);
以上是行的情况,接下来我们需要将矩阵行列置换一下,求一下列的状态即可
具体做法就是i换成j,j换成i就可以了(
最终代码如下:
点击查看代码
#include <bits/stdc++.h>
using ll = int64_t;
const ll N = 2e5 + 10;
const ll INF = LLONG_MAX;
const ll mod = 998244353;
// 核心:行列操作互不影响
// 考虑dp, 则有:
// 1. f[i][0] = std::min(f[i - 1][0], f[i - 1][1])
// 2. f[i][1] = std::min(f[i - 1][0] + a[i], f[i - 1][1] + a[i])
// 这道题所具有的特殊情况为:
// 1. 如果该行比上一行多1,那么上一行不能动
// 2. 如果该行比上一行少1,那么该行不能动
void solve () {
int n;
std::cin >> n;
std::vector h(n + 1, std::vector<ll>(n + 1));
std::vector<ll> a(n + 1), b(n + 1);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
std::cin >> h[i][j];
}
}
for (int i = 1; i <= n; i++) {
std::cin >> a[i];
}
for (int i = 1; i <= n; i++) {
std::cin >> b[i];
}
std::vector f1(n + 1, std::vector<ll>(2, INF));
std::vector f2(n + 1, std::vector<ll>(2, INF));
f1[1][0] = 0, f1[1][1] = a[1];
f2[1][0] = 0, f2[1][1] = b[1];
ll ans = 0;
// row
for (int i = 2; i <= n; i++) {
int x = 1, y = 1, z = 1;
for (int j = 1; j <= n; j++) {
ll d = h[i][j] - h[i - 1][j];
if (d == 1) x = 0;
if (d == 0) y = 0;
if (d == -1) z = 0;
}
// 当不存在“第i-1行比第i行少1”的情况时
if (x) f1[i][0] = std::min(f1[i][0], f1[i - 1][1]);
// 当不存在“第i-1行和第i行相同”的情况时
if (y) f1[i][0] = std::min(f1[i][0], f1[i - 1][0]);
if (y) f1[i][1] = std::min(f1[i][1], f1[i - 1][1] + a[i]);
// 当不存在“第i-1行比第i行多1”的情况时
if (z) f1[i][1] = std::min(f1[i][1], f1[i - 1][0] + a[i]);
}
ans += std::min(f1[n][1], f1[n][0]);
// col
for (int j = 2; j <= n; j++) {
int x = 1, y = 1, z = 1;
for (int i = 1; i <= n; i++) {
ll d = h[i][j] - h[i][j - 1];
if (d == 1) x = 0;
if (d == 0) y = 0;
if (d == -1) z = 0;
}
if (x) f2[j][0] = std::min(f2[j][0], f2[j - 1][1]);
if (y) f2[j][0] = std::min(f2[j][0], f2[j - 1][0]);
if (y) f2[j][1] = std::min(f2[j][1], f2[j - 1][1] + b[j]);
if (z) f2[j][1] = std::min(f2[j][1], f2[j - 1][0] + b[j]);
}
ans += std::min(f2[n][0], f2[n][1]);
if (ans >= INF) std::cout << -1 << '\n';
else std::cout << ans << '\n';
}
int main () {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
std::cin >> t;
while (t--) {
solve();
}
return 0;
}
第二题的话是一个Div.4的G题,Round_1017
https://codeforces.com/problemset/problem/2094/G
这道题的话,给你了三种操作,让你每次操作后输出序列a的一个加权sum,其中sum = ∑ (a[i] * i)
三种操作分别是:
- 对数组进行循环移位。也就是说,数组 [a1, a2, …, an] 变成 [an, a1, a2, …, an−1].
- 反转整个数组。即数组 [a1, a2, …, an] 变为 [an, an−1, …, a1].
- 在数组末尾添加一个元素。在数组的末尾添加 k之后,数组 [a1, a2, …, an] 变为 [a1, a2, …, an, k]
可以看到,这道题的话用deque会很舒服
可以同时实现push_back()、pop_front()、pop_back()、reverse()等操作
然后博主喜提TLE了……
思来想去不知怎么写,万般无奈之下又点开了题解
这道题的操作次数是q<=2e5,显然不能暴力
那么怎么办呢?
显然我们发现,每次加入k时sum的变化,是可以推导出来的
我们假定sum为序列的加权和,tmp为序列的和
那么我们可以推导出,在操作1时,sum发生了这样的变化:
sum += tmp - a.back();
sum -= a.back() * (a.size() - 1);
因为我们是加权和嘛,所以每次序列循环移位时,每一位的索引都发生了变化,除了最后一位都增加了1
那么这不就是sum = sum + tmp - a.back()了
同样的,因为我们把back推到front了,此时索引由a.size()变成了1,所以sum = sum - a.back() * (a.size() - 1)
对于操作3那更简单了,直接sum += k * a.size()即可
那么问题来了,操作2的逆置该如何实现呢?
显然,如果我们直接调用reverse函数,会导致前面的结果全都变得没用,重新计算的话还会超时
这个时候,我们可以提前开一个re_sum,只要让re_sum和sum的所有操作都相反就可以了!!
sum正推我倒推,sum用push_back()的时候,我re_sum就push_front()就好了!
那么在输出的时候,我们仅需判断一下当前该输出sum还是re_sum就ok了
博主的原代码如下(debug了一万年,所以代码极其丑陋)
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
// GNU G++17 7.3.0
using std::cin, std::cout;
#define debug0(x) cout << #x << " = " << x << '\n'
#define debugp(x, y) cout << #x << " = " << x << ", " << #y << " = " << y << '\n'
#define debugt(x, y, z) cout << #x << " = " << x << ", " << #y << " = " << y << ", " << #z << " = " << z << '\n'
#define debug1(f, a, b) cout << #f << ": "; for (int i = (a); i <= (b); i++) cout << (f)[i] << " \n"[i == (b)]
#define debug2(f, a, b, c, d) cout << #f << ":\n"; for (int i = (a); i <= (b); i++) for (int j = (c); j <= (d); j++) cout << (f)[i][j] << " \n"[j == (d)]
#define debug3(q) cout << #q << ": "; for (auto it : (q)) cout << it << ' '; cout << '\n'
#define debug4(q) cout << #q << ":\n"; for (auto [x, y] : (q)) cout << '[' << x << ", " << y << "]\n"
#define debug5(q) cout << #q << ":\n"; for (auto [x, y, z] : (q)) cout << '[' << x << ", " << y << ", " << z << "]\n"
using ll = int64_t;
const ll N = 2e5 + 10;
const ll INF = LLONG_MAX;
const ll mod = 998244353;
void solve () {
ll q;
std::cin >> q;
std::deque<ll> a;
std::deque<ll> re_a;
ll tmp = 0, re_tmp = 0;
ll sum = 0, re_sum = 0;
ll flag = 0;
while (q--) {
int op;
std::cin >> op;
if (op == 1) {
if (flag % 2 == 0) {
sum += tmp - a.back();
sum -= a.back() * (a.size() - 1);
re_sum -= re_tmp - re_a.front();
re_sum += re_a.front() * (re_a.size() - 1);
a.push_front(a.back());
a.pop_back();
re_a.push_back(re_a.front());
re_a.pop_front();
}
else {
re_sum += re_tmp - re_a.back();
re_sum -= re_a.back() * (re_a.size() - 1);
sum -= tmp - a.front();
sum += a.front() * (a.size() - 1);
re_a.push_front(re_a.back());
re_a.pop_back();
a.push_back(a.front());
a.pop_front();
}
if (flag % 2 == 0) std::cout << sum << '\n';
else std::cout << re_sum << '\n';
// debug3(a);
// debug3(re_a);
// debugp(sum, re_sum);
// std::cout << '\n';
}
else if (op == 2) {
// 其实这里用std::swap()就可以解决了!!
flag++;
if (flag % 2 == 0) std::cout << sum << '\n';
else std::cout << re_sum << '\n';
// debug3(a);
// debug3(re_a);
// debugp(sum, re_sum);
// std::cout << '\n';
}
else if (op == 3) {
ll k;
std::cin >> k;
if (flag % 2 == 0) {
a.push_back(k);
re_a.push_front(k);
sum += k * a.size();
tmp += k;
re_sum += k + re_tmp;
re_tmp += k;
}
else {
re_a.push_back(k);
a.push_front(k);
re_sum += k * a.size();
re_tmp += k;
sum += k + tmp;
tmp += k;
}
if (flag % 2 == 0) std::cout << sum << '\n';
else std::cout << re_sum << '\n';
// debug3(a);
// debug3(re_a);
// debugp(sum, re_sum);
// std::cout << '\n';
}
}
}
int main () {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
std::cin >> t;
while (t--) {
solve();
}
return 0;
}
不过博主后来又意识到可以用std::swap(),这样的话可以简化很多
点击查看代码
#include <bits/stdc++.h>
using ll = int64_t;
const ll N = 2e5 + 10;
const ll INF = 1e18 + 7;
const ll mod = 998244353;
void solve () {
ll q;
std::cin >> q;
std::deque<ll> a;
std::deque<ll> re_a;
ll tmp = 0, re_tmp = 0;
ll sum = 0, re_sum = 0;
while (q--) {
int op;
std::cin >> op;
if (op == 1) {
sum += tmp - a.back();
sum -= a.back() * (a.size() - 1);
re_sum -= re_tmp - re_a.front();
re_sum += re_a.front() * (re_a.size() - 1);
a.push_front(a.back());
a.pop_back();
re_a.push_back(re_a.front());
re_a.pop_front();
std::cout << sum << '\n';
}
else if (op == 2) {
std::swap(sum, re_sum);
std::swap(tmp, re_tmp);
std::swap(a, re_a);
std::cout << sum << '\n';
}
else if (op == 3) {
ll k;
std::cin >> k;
a.push_back(k);
re_a.push_front(k);
sum += k * a.size();
tmp += k;
re_sum += k + re_tmp;
re_tmp += k;
std::cout << sum << '\n';
}
}
}
int main () {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
std::cin >> t;
while (t--) {
solve();
}
return 0;
}
今天拼尽全力吃下的两道1700可算是消化了
其实还过了一道1600,但那个是小号写过,为了检验一下自己是否学会了,索性用大号交了几发
很简单的构造,感觉完全不该有1600
然后就是刚才秒掉的那个1500的题了
是一场Div.2的C,https://codeforces.com/problemset/problem/2108/C
这道题的意思是,给定了一个序列,每次只能递减的标记,要求所有位置都被标记上
那么我们可以将所有的数字具象化一下,用图形来表示是这样的:
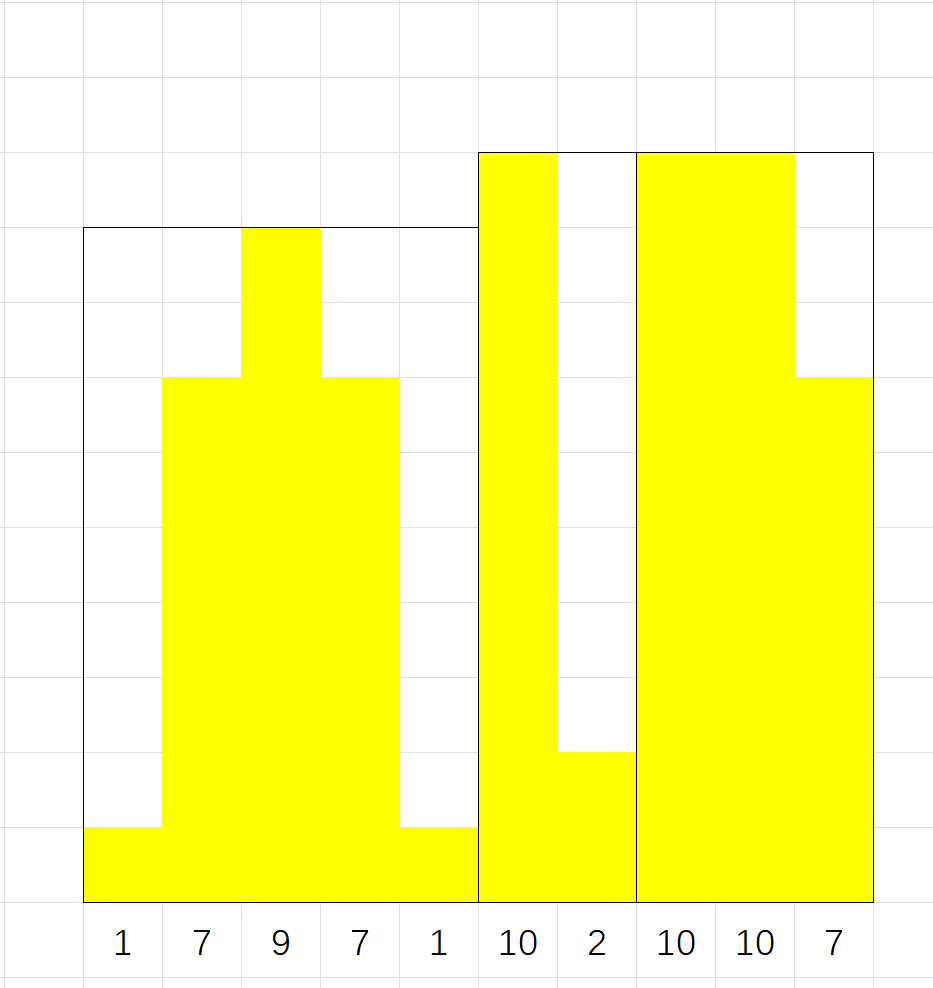
那么我们的问题就很简单了:去数一下有多少座“山峰”就ok了
代码如下:
点击查看代码
#include <bits/stdc++.h>
using ll = int64_t;
const ll N = 2e5 + 10;
const ll INF = LLONG_MAX;
const ll mod = 998244353;
void solve () {
int n;
std::cin >> n;
std::vector<int> a(n + 1, -1);
for (int i = 1; i <= n; i++) {
std::cin >> a[i];
}
if (n == 1) {
std::cout << 1 << '\n';
return;
}
int ans = 0;
int i = 1;
while (i < n) {
while (a[i] <= a[i + 1]) i++;
ans++;
while (a[i] >= a[i + 1]) i++;
}
std::cout << ans << '\n';
}
int main () {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
std::cin >> t;
while (t--) {
solve();
}
return 0;
}
(第一遍没特判,所以WA了一发)
当时两遍过的时候真的很震惊,因为我那个思路属实有点忒简单了
也可能是瞎猫碰上死耗子,凑巧会写这道题吧,但无论如何,我的信心确实增长了一些(
看来板刷1600真的有用,感觉思维慢慢变得灵活了
今天是第二天,希望这次一定要坚持下去


 浙公网安备 33010602011771号
浙公网安备 33010602011771号