[题解]P6560 [SBCOI2020] 时光的流逝

思路

标准博弈论，我们假定 $dp_i$ 表示当前棋子在 $i$ 的时候，先手必赢为 $1$，先手必负为 $-1$，无法确定为 $0$。

那么我们看图分析一下：

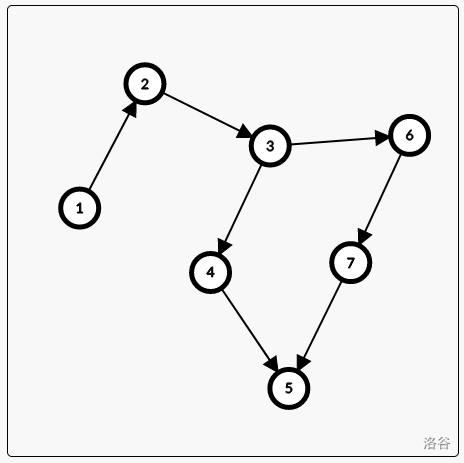
在终点为 $5$ 的情况下：不难的出 $dp_5 = 1,dp_4 = -1,dp_7 = -1,dp_3 = -1\cdots$。

根据这些，我们便不难想到转移公式：

$$\left\{\begin{matrix} dp_i = 1 & \exists v,(i,v) \in E,dp_v = -1 \\ dp_i = -1 & \forall v,(i,v) \in E,dp_v = 1 \end{matrix}\right.$$

看到这里，我们不难想到拓扑排序。但是，拓扑排序只能在 DAG 上做，可是这里有环，只有转换一下。

我们知道，如果在一个有向有环图中跑一边拓扑排序，只会剩下环。

然而，对于剩下的这个环 $G_h(V_h,E_h)$，当 $dp_{i} \neq 0,i \in V_h$ 时，就是会产生解的，否则不行。

需要注意的是，这种做法需要反向建边。

Code

#include <bits/stdc++.h>  
#define re register  
  
using namespace std;  
  
const int N = 1e5 + 10,M = 5e5 + 10;  
int n,m,q,idx;  
int h[N],ne[M],e[M];  
int pre[N],in[N],dp[N];  
  
inline int read(){  
    int r = 0,w = 1;  
    char c = getchar();  
    while (c < '0' || c > '9'){  
        if (c == '-') w = -1;  
        c = getchar();  
    }  
    while (c >= '0' && c <= '9'){  
        r = (r << 3) + (r << 1) + (c ^ 48);  
        c = getchar();  
    }  
    return r * w;  
}  
  
inline void add(int a,int b){  
    ne[idx] = h[a];  
    e[idx] = b;  
    h[a] = idx++;  
}  
  
inline void tp_sort(int E){  
    queue<int> Q;  
    for (re int i = 1;i <= n;i++){  
        if (!in[i] || i == E){  
            dp[i] = -1;  
            Q.push(i);  
        }  
    }  
    while (!Q.empty()){  
        int t = Q.front();  
        Q.pop();  
        for (re int i = h[t];~i;i = ne[i]){  
            int j = e[i];  
            if (dp[j] == 1) continue;  
            if (dp[t] == 1){  
                in[j]--;  
                if (!in[j]){  
                    dp[j] = -1;  
                    Q.push(j);  
                }  
            }  
            else{  
                dp[j] = 1;  
                Q.push(j);  
            }  
        }  
    }  
}  
  
int main(){  
    memset(h,-1,sizeof(h));  
    n = read();  
    m = read();  
    q = read();  
    for (re int i = 1;i <= m;i++){  
        int a,b;  
        a = read();  
        b = read();  
        add(b,a);  
        pre[a]++;  
    }  
    while (q--){  
        int S,E;  
        memset(dp,0,sizeof(dp));  
        memcpy(in,pre,sizeof(pre));//多测清空   
        S = read();  
        E = read();  
        tp_sort(E);//拓扑排序   
        printf("%d\n",dp[S]);  
    }  
    return 0;  
}