[题解]GYM 101196H Vin Diagrams

题意

给定一个 $n \times m$ 的字符矩阵 $a$。

在矩阵中有两个集合，每个集合的边界是 X（特别的，每个集合有一个点是 A 或 B）。

这两个集合组成了一个维恩图，现在求两个集合的补集，以及并集。（也就是 . 的数量）

注意：

1. 保证了两个集合的两个交点一定是形如下图的：

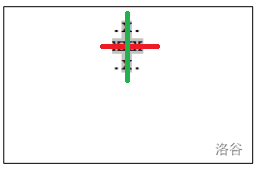
保证了任意两个 `X` 不可能出现形如下图的情况：

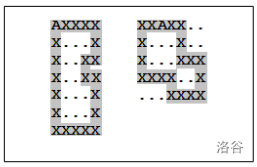
思路

首先先 DFS 出两个集合的边界。

其中遇到交点时，继续按照原方向走，一定能保证最后的图形是当前集合。并将标记出的两个集合的边界分别记录在 $vis_1$ 与 $vis_2$ 中。

然后，不难发现，对于两个集合中靠左的集合边界的左上角的点 $(ax,ay)$，向右下角走一步一定能走到集合内部（即 $(ax + 1,ay + 1)$）。

同理，对于靠右集合右上角的点 $(bx,by)$，向左下角一定能走到集合内部（即 $(bx + 1,by - 1)$）。

随后，分别以这两个点为起点 DFS，并分别以 $vis_1,vis_2$ 中记录的边界为边界。然后将经过的点分别用 $st_1,st_2$ 标记。

不难发现，对于 $a_{i,j}$ 是 . 时，可以分为 $3$ 中情况：

1. $st_{1,i,j} \wedge st_{2,i,j}$ 时，一定是两集合的并集，所以 $ansc$ 加 $1$。
2. $st_{1,i,j} \wedge \neg st_{2,i,j}$ 时，一定是 A 集合的补集，所以 $ansa$ 加 $1$。
3. $\neg st_{1,i,j} \wedge st_{2,i,j}$ 时，一定是 B 集合的补集，所以 $ansb$ 加 $1$。

Code

#include <bits/stdc++.h>  
#define re register  
  
using namespace std;  
  
const int N = 110,inf = 1e9 + 10;  
int n,m,sax,say,sbx,sby;  
int ax = inf,ay = inf,bx = inf,by = -inf;  
int ansa,ansb,ansc;  
int dx[] = {0,1,-1,0,0};  
int dy[] = {0,0,0,1,-1};  
char arr[N][N];  
bool vis[5][N][N],st[5][N][N];  
  
inline int read(){  
    int r = 0,w = 1;  
    char c = getchar();  
    while (c < '0' || c > '9'){  
        if (c == '-') w = -1;  
        c = getchar();  
    }  
    while (c >= '0' && c <= '9'){  
        r = (r << 3) + (r << 1) + (c ^ 48);  
        c = getchar();  
    }  
    return r * w;  
}  
  
inline void dfs(int x,int y,int l,bool vis[][N]){  
    bool falg = false;  
    vis[x][y] = true;  
    for (re int i = 1;i <= 4;i++){  
        int tx = x + dx[i];  
        int ty = y + dy[i];  
        if (arr[tx][ty] != 'X' && arr[tx][ty] != 'A' && arr[tx][ty] != 'B'){  
            falg = true;  
            break;  
        }  
    }  
    if (falg){  
        for (re int i = 1;i <= 4;i++){  
            int tx = x + dx[i];  
            int ty = y + dy[i];  
            if (tx >= 1 && tx <= n && ty >= 1 && ty <= m && arr[tx][ty] != '.' && !vis[tx][ty]) dfs(tx,ty,i,vis);  
        }  
    }  
    else{  
        int tx = x + dx[l];  
        int ty = y + dy[l];  
        if (tx >= 1 && tx <= n && ty >= 1 && ty <= m && arr[tx][ty] != '.' && !vis[tx][ty]) dfs(tx,ty,l,vis);  
    }  
}  
  
inline void dfs1(int x,int y){  
    st[1][x][y] = true;  
    for (re int i = 1;i <= 4;i++){  
        int tx = x + dx[i];  
        int ty = y + dy[i];  
        if (tx >= 1 && tx <= n && ty >= 1 && ty <= m && !vis[1][tx][ty] && !st[1][tx][ty]) dfs1(tx,ty);  
    }  
}  
  
inline void dfs2(int x,int y){  
    st[2][x][y] = true;  
    for (re int i = 1;i <= 4;i++){  
        int tx = x + dx[i];  
        int ty = y + dy[i];  
        if (tx >= 1 && tx <= n && ty >= 1 && ty <= m && !vis[2][tx][ty] && !st[2][tx][ty]) dfs2(tx,ty);  
    }  
}  
  
int main(){  
    n = read();  
    m = read();  
    for (re int i = 1;i <= n;i++){  
        scanf("%s",arr[i] + 1);  
        for (re int j = 1;j <= m;j++){  
            if (arr[i][j] == 'A'){  
                sax = i;  
                say = j;  
            }  
            else if (arr[i][j] == 'B'){  
                sbx = i;  
                sby = j;  
            }  
        }  
    }  
    dfs(sax,say,1,vis[1]);//标记边界   
    dfs(sbx,sby,1,vis[2]);  
    for (re int i = 1;i <= n;i++){  
        for (re int j = 1;j <= m;j++){  
            if (vis[1][i][j]){//找 (ax,ay) 与 (bx,by)   
                if (ax > i){  
                    ax = i;  
                    ay = j;  
                }  
                else if (ax == i && ay > j) ay = j;  
            }  
            if (vis[2][i][j]){  
                if (bx > i){  
                    bx = i;  
                    by = j;  
                }  
                else if (bx == i && by < j) by = j;  
            }  
        }  
    }  
    dfs1(ax + 1,ay + 1);  
    dfs2(bx + 1,by - 1);  
    for (re int i = 1;i <= n;i++){//更新答案   
        for (re int j = 1;j <= m;j++){  
            if (st[1][i][j] && st[2][i][j] && arr[i][j] == '.') ansc++;  
            else if (st[1][i][j] && arr[i][j] == '.') ansa++;  
            else if (st[2][i][j] && arr[i][j] == '.') ansb++;  
        }  
    }  
    printf("%d %d %d",ansa,ansb,ansc);  
    return 0;  
}