[题解]CF1811F Is It Flower&

思路

观察一下，发现对于一个拥有 $n$ 个节点的 $k$ -flowers，$k$ 一定为 $\sqrt n$。

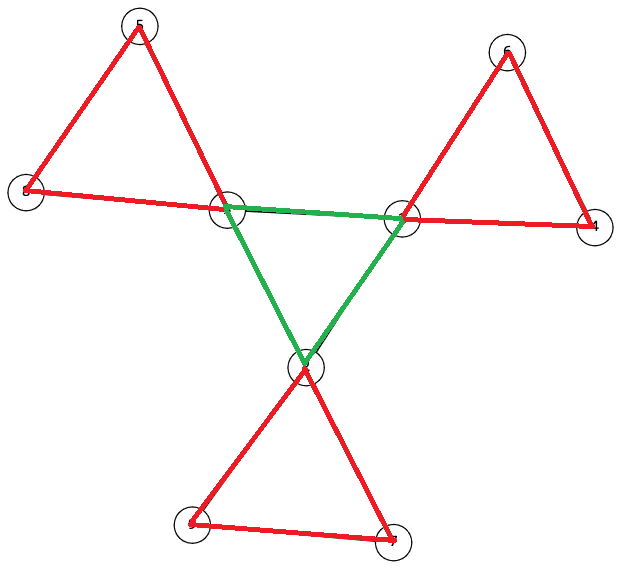
因为考虑只观察图中标红区域，对于一个 $k$ -flowers，一定会有 $k$ 个，并且它们的大小均为 $k$，而总节点数为 $n$，因此 $k = \sqrt n$。所以，如果 $n$ 不是完全平方数，则不是 $k$ -flower。同时，我们可以发现如果某一个标红区域的大小不为 $k$ 也不是 $k$ -flower。如果度数为 $2$ 的点数量不为 $n - k$ 也不是 $k$ -flower。

继续观察，发现所有在绿色区域的节点度数均为 $4$，其余节点度数均为 $2$，并且绿色区域的点的数量一定是 $k$。

继续观察图中绿色区域，对于所有在绿色区域中的节点，都有两条连向绿色区域点的边，有两条连向红色区域的边，并且度数为 $4$。因此如果在绿色区域中的点没有两条连向绿色区域的点，或者没有连向两条只在红色区域的点就不是 $k$ -flower。

当然，如果图都不连通，显然也是不行的。

Code

#include <bits/stdc++.h>  
#define re register  
  
using namespace std;  
  
const int N = 2e5 + 10;  
int n,m,sz;  
int d[N],f[N];  
bool vis[N];  
vector<int> g[N];  
  
inline int read(){  
    int r = 0,w = 1;  
    char c = getchar();  
    while (c < '0' || c > '9'){  
        if (c == '-') w = -1;  
        c = getchar();  
    }  
    while (c >= '0' && c <= '9'){  
        r = (r << 3) + (r << 1) + (c ^ 48);  
        c = getchar();  
    }  
    return r * w;  
}  
  
inline int find(int x){  
    if (f[x] != x) return f[x] = find(f[x]);  
    return f[x];  
}  
  
inline void merge(int a,int b){  
    int x = find(a),y = find(b);  
    if (x == y) return;  
    f[x] = y;  
}  
  
inline void dfs(int u){  
    sz++;  
    vis[u] = true;  
    for (auto v:g[u]){  
        if (!vis[v]) dfs(v);  
    }  
}  
  
inline void solve(){  
    n = read();  
    m = read();  
    for (re int i = 1;i <= n;i++){  
        d[i] = 0;  
        f[i] = i;  
        vis[i] = false;  
        g[i].clear();  
    }  
    for (re int i = 1;i <= m;i++){  
        int a,b;  
        a = read();  
        b = read();  
        merge(a,b);  
        d[a]++;  
        d[b]++;  
        g[a].push_back(b);  
        g[b].push_back(a);  
    }  
    int k = sqrt(n);  
    if (k * k != n) return puts("NO"),void();  
    int a = 0,b = 0,t = find(1);  
    for (re int i = 1;i <= n;i++){  
        if (find(i) != t) return puts("NO"),void();  
        a += (d[i] == 2);  
        b += (d[i] == 4);  
    }  
    if (b != k || a + b != n) return puts("NO"),void();  
    for (re int i = 1;i <= n;i++){  
        if (d[i] != 4) continue;  
        int a = 0,b = 0;  
        for (auto u:g[i]){  
            a += (d[u] == 2);  
            b += (d[u] == 4);  
        }  
        if (a != 2 || b != 2) return puts("NO"),void();  
        for (auto u:g[i]){  
            if (d[u] == 2){  
                sz = 0;  
                vis[i] = true;  
                dfs(u);  
                break;  
            }  
        }  
        if (sz != k - 1) return puts("NO"),void();  
    }  
    puts("YES");  
}  
  
int main(){  
    int T;  
    T = read();  
    while (T--) solve();  
    return 0;  
}