数学作业

1.1

（1）

特征多项式 \((1-\lambda)(3-\lambda)^2\)。

特征值 \(\lambda_1 = 1, \lambda_2 = \lambda_3 = 3\)。
对应的一种特征向量为

\[v_1 = \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}, v_2 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, v_3 = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \]

对角化：
取

\[X= \begin{pmatrix} 1 & 0 & 1 \\ -1 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}, X^{-1}= \begin{pmatrix} \frac 1 2 & -\frac 1 2 & 0\\ 0 & 0 & 1 \\ \frac 1 2 & \frac 1 2 & 0 \end{pmatrix}, \Lambda = \begin{pmatrix} 1 & & \\ & 3 & \\ & & 3 \\ \end{pmatrix} \]

故

\[A=X\Lambda X^{-1} \]

（2）

特征多项式：\(\lambda(\lambda^2+3)\).

特征值 \(\lambda_1 = 0, \lambda_2 = \sqrt{3}i, \lambda_3 =- {\sqrt 3i}\)。
特征向量

\[v_1 = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}, v_2 = \begin{pmatrix} 1 \\ \frac{-1+\sqrt 3i}2 \\ \frac{-1-\sqrt 3i} 2 \end{pmatrix}, v_3 = \begin{pmatrix} 1 \\ \frac{-1-\sqrt 3i}2 \\ \frac{-1+\sqrt 3i} 2 \end{pmatrix} \]

对角化，其中

\[X = \begin{pmatrix} 1 & 1 & 1 \\ 1 & \frac{-1+\sqrt 3i} 2 & \frac{-1-\sqrt 3i}2 \\ 1 & \frac{-1-\sqrt 3i}2 & \frac{-1+\sqrt 3i}2 \end{pmatrix} ,X^{-1} = \frac{1}{3} \begin{pmatrix} 1 & 1 & 1 \\ 1 & \frac{-1 - \sqrt{3}\,i}{2} & \frac{-1 + \sqrt{3}\,i}{2} \\ 1 & \frac{-1 + \sqrt{3}\,i}{2} & \frac{-1 - \sqrt{3}\,i}{2} \end{pmatrix} ,\Lambda=\begin{pmatrix} 1 & & \\ & \sqrt 3i & \\ & & -\sqrt 3i \end{pmatrix} \]

（3）

特征多项式为 \(-\lambda(\lambda-9)^2\)，特征值为 \(\lambda_1 = 0, \lambda_2 = \lambda_3 = 9\)。

对应可能的特征向量为

\[v_1 = \begin{pmatrix} 1 \\ 2 \\ -2 \end{pmatrix} , v_2 = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}, v_3 = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \]

故对角化

\[X = \begin{pmatrix} 1 & 0 & 1 \\ 2 & 1 & 0 \\ -2 & 1 & 1 \end{pmatrix}, X^{-1} = \frac 15\begin{pmatrix} 1 & 1 & -1 \\ -2 & 3 & 2 \\ 4 & -1 & 1 \end{pmatrix}, \Lambda = \begin{pmatrix} 0 & & \\ & 9 & \\ & & 9 \end{pmatrix} \]

1.2

命题 1

证明：

记特征多项式为 \(f(\lambda)\)。回顾特征多项式的来源，即为 \(\det (\lambda I-A)\)。而 \(\lambda\) 的 \(n-1\) 次项系数，只能从行列式的 \(\prod_{i=1}^n (\lambda-a{ii})\) 项贡献而来。

将这一项展开，取 \(\lambda^{n-1}\) 的系数，显然就是 \(-\sum a_{ii}\)。
由题设结论，\(\Box\)

命题 2

证明：

记特征多项式为 \(f(\lambda)\)。由上面的关系，\(\prod \lambda_i\) 即为特征多项式的常数项乘 \((-1)^n\)，也就是 \(\prod \lambda_i=f(0)\times(-1)^n=\det (0 \cdot I-A) \times (-1)^n = \det A\)。
\(\Box\)

1.3

记 \(A\) 的特征多项式 \(f(\lambda)\) 的各项系数为 \(a_0,a_1,\dots,a_{n-1}\)。这里常数项 \(a_0=\det A \ne 0\)。

由 Cayley-Hamilton 定理，\(f(A)=O\)。

这里构造一个 \(b_i = -\frac{a_i}{a_0}(i = 1,2,\dots,n-1)\)，特殊地，\(b_n=0\)。这时候注意到

\[\begin{aligned} & \ \sum_{i=1}^n b_iA^i \\ = & \ -\sum_{i=0}^{n-1}\frac{a_i}{a_0}A^i + I\\ = & \ -\frac{f(A)}{a_0} + I\\ = & \ O + I\\ = & \ I \end{aligned} \]

故令 \(c_i = b_{i+1},(i=0,1,\dots,n-1)\)，两边同时右乘 \(A^{-1}\)，证毕。

2.1

即证，\(Px \perp v\)，即 \((I-vv^T)x \cdot v = 0\)。
这里即证，\(v\cdot x = vv^Tx \cdot v\)。

设

\[v=\begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} \]

则 \((vv^T)_{ij}=v_iv_j\)。
故 \((vv^Tx)_{i}=\sum_{k=1}^n v_iv_kx_k=v_i(v \cdot x)\)。
则 \((vv^Tx）\cdot v = \sum_{i=1}v_i(v \cdot x)=(v\cdot x)\sum_{i=1}v_i^2\)。
又因为 \(|v|=1\)，故上式等于 \(v\cdot x\)，得证。

2.2

\(P\) 空间是 \(n-1\) 维的。可以在里面找到 \(n-1\) 个互不线性相关的向量。
然后显然这些向量左乘 \(P\) 都等于自身。（由投影的性质）

所以这 \(n-1\) 个向量都是 \(P\) 的特征向量。这些特征向量对应的特征值都是 \(1\)。
所以 \(1\) 的重数至少是 \(n-1\)（u群大手子指出这是对的）。

最后，\(\lambda=0\) 显然是一个可行解。
以上。

• 几何意义：

回忆特征值最初的定义。即，存在向量 \(v\) 满足 \(Pv=\lambda v\)。而 \(Pv\) 就是 \(v\) 在 \(P\) 空间内的投影。

即，\(v\) 投影之后仍然与 \(v\) 共线。
不难发现，若 \(\lambda\ne 0\)，则 \(v\) 一定在 \(P\) 空间内。而由投影的意义，\(Pv=v\)。故 \(\lambda=1\)。
若 \(\lambda =0\)，则 \(v\) 与 \(P\) 空间垂直，即与其法向量共线。

2.3

令 \(A=I-xx^T\)。
由上面的结论，\(A\) 的特征多项式 \(p_A(\lambda)=\lambda(\lambda-1)^{n-1}\)。

然后注意到待求的行列式就是 \(p_A(2)=2 \times 1^{n-1}=2\)。

3.1

记 \(B=A^*A\)。由定义，\(B_{ij}=\sum_{k=1}^n A^*_{ik}A_{kj}\)。

\(i=j\) 时，由行列式的定义。\(B_{ij}=\det A\)。

\(i\ne j\) 时，由上面的定义。

\[\det A = \sum_{k=1}A^*_{ik}A_{ki}\]

并且一行减去另一行，行列式和 \(A^*\) 显然都不变。

\[\det A = \sum_{k=1}A^*_{ik}(A_{ki}-A_{kj}) \]

两式相减可得 \(B_{ij}=0\)。
\(\Box\)

3.2

有

\[\begin{aligned} p_A(\lambda)I&=\sum_{k=0}^{n-1}B_k\lambda^k(\lambda I-A)\\ &= \sum_{k=0}^{n-1}B_k\lambda^{k+1}-\sum_{k=0}^{n-1}B_k\lambda^kA\\ &= \sum_{k=0}^{n}B_{k-1}\lambda^{k}-\sum_{k=0}^{n}B_k\lambda^kA\\ &= \lambda^k\sum_{k=0}^{n}(B_{k-1}-B_k A)\\ \end{aligned} \]

比较系数显然得证。

3.3

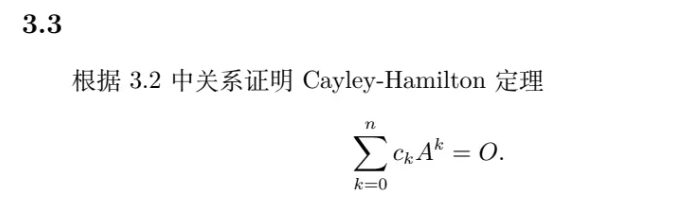
由 3.2，

\[\begin{aligned} \sum_{k=0}^n c_kA^k &=\sum_{k=0}^n{-B_kA^{k+1}+B_{k-1}A^k} \\ & = B_{-1}A^0-B_0A^1+B_0A^1-B_1A^2+B_1A^2-\dots-B_nA^{n+1} \\ & = B_{-1}A^0-B^nA^{n+1} \\ & = OA^0-OA^{n+1} \\ & = O \end{aligned} \]