Atcoder ABC395 题解

ABC395

A

判断有没有 \(1 \le i < n\)，满足 \(a_i \ge a_{i+1}\)。有则 No，没有则 Yes。

submission.

B

随便递归一下，每层传入当前要覆盖的子矩阵的左上角坐标 \((x, y)\)，正方形大小 \(n\)，以及需要覆盖的字符 \(p\)。每次把这个子矩阵覆盖一遍，然后 \((x, y) \gets (x+1, y+1),n \gets n-2, p = \neg p\)。

submission.

C

显然最短的好的子数组一定要首尾相同，否则可以再缩。
于是用一个桶存下当前元素的上一个出现位置，这个位置到当前下标 \(i\) 就是可能的答案区间。

submission.

D

画图理解。
先放代码：
submission.

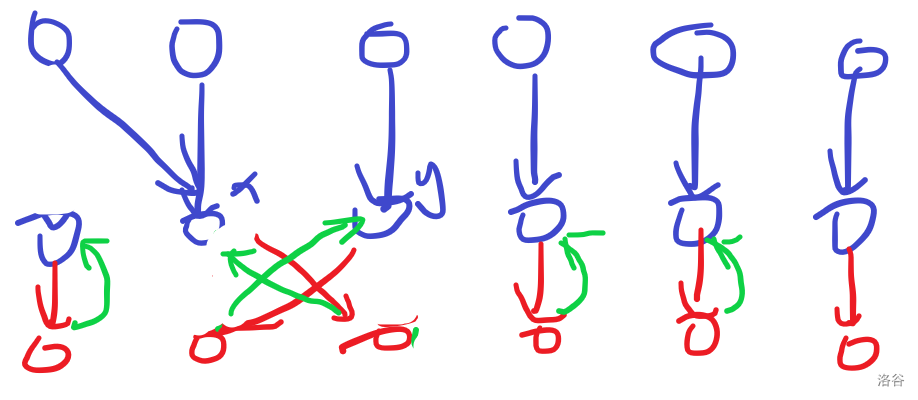
蓝线表示 \(pos\) 的映射关系，红线表示 \(ans\) 的映射关系，绿线表示 \(virt\) 的映射关系。

难搞的就是 swap 操作。我们不需要换鸽子，只需换巢上面贴的数字，即 \(ans\) 的映射关系。\(virt\) 和 \(ans\) 互为相反映射。

E

建图：

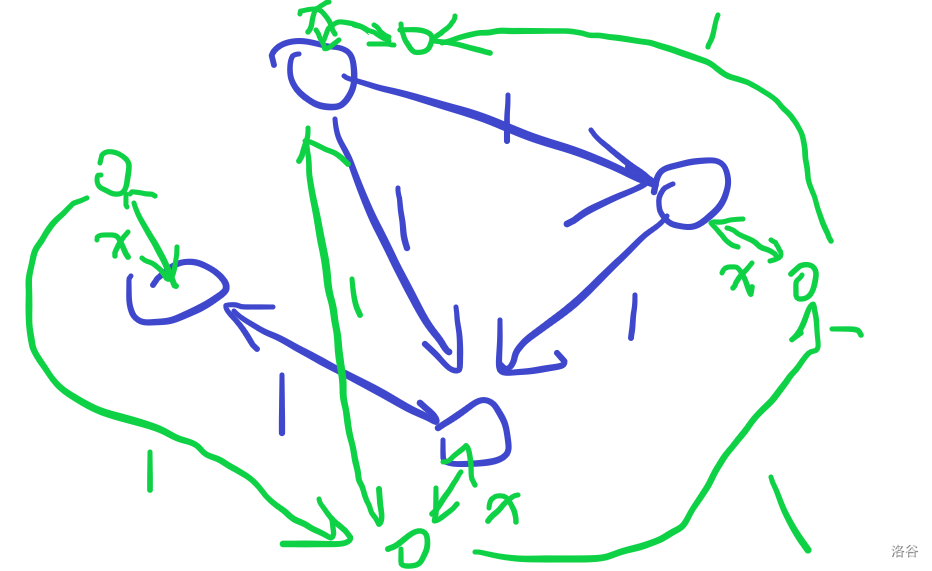
也就是拆点。

蓝色边表示原始有向图。
这样拆点就可以保证不进行 reverse 操作时，不需走 \(x\) 边；reverse 时，一定要走 \(x\) 边。

然后就是 Dijkstra 的模板。
答案就是 \(\min(dis_n, dis_{n'})\)。

F

注意到 \(H\) 越小，越有可能有解；同时，\(H\) 越大，答案越优。我们只需要二分最大的符合答案 \(H\)。
至于 check 函数，我们可以从算出当前 \(u_i\) 不考虑 \(x\) 的限制可能取值的区间 \([l_i, r_i]\)。维护一个区间 \([L, R]\) 表示上一个 \(u\) 最终可能的区间，从 \(1\) 到 \(n\) 扫一遍，考虑 \(x\) 限制，\(u_i\) 的最终取值一定是前一个 \([u_{i-1}-x, u_{i-1}+x]\)。对应到 \(u_{i-1}\) 的区间，那么 \(u_i\) 除了要属于 \([l_i, r_i]\)，还要属于 \([L-x, R+x]\)。
于是 \([L, R] \gets [L-x, R+x] \cap [l_i, r_i]\)。
如果 \([L, R]\) 是空区间，那就无解。

形式上可以写成三分。
submission.

G

不会。