网络流学习记录
跟开了森林书一样。
最大流
概念
有一个有源点 \(s\) 和有汇点 \(t\) 的有向图(网络),边上有【容量】。想象一下,我们从 \(s\) 灌进无限的水,水能从有向路径到达 \(t\),而每条路径最多允许通过【容量】的水。最终从 \(t\) 流出的水即是最大流。
有点抽象,举个例子:
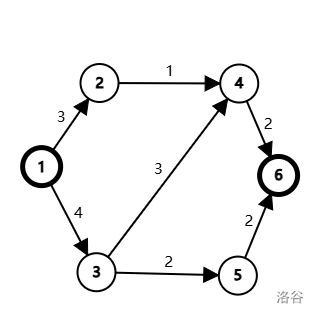
这里有一个源点为 \(1\),汇点为 \(6\) 的网络。我们从 \(1\) 至 \(6\) 有 \(3\) 条路径可以走:\(1 \to 2 \to 4 \to 6,1 \to 3 \to 5 \to 6,1 \to 3 \to 4 \to 6\)。
首先,我们走 \(1 \to 2 \to 4 \to 6\) 这条路径,可以通过 \(1\) 的水(即路径最小值)。
其次,我们走 \(1 \to 3 \to 4 \to 6\) 这条路径,可以通过 \(1\) 的水。(\(4 \to 6\) 这条边已经有 \(1\) 的水流过了,还剩 \(1\) 的容量)。
最后,我们走 \(1 \to 3 \to 5 \to 6\) 这条路径,可以通过 \(2\) 的水。
这种方案是最优的(之一)。故该网络的最大流为 \(1+1+2=4\)。
解法
Ford–Fulkerson 方法
这是【贪心】算法在网络流上的总称。
我们首先考虑以下贪心:有路径可流,就往下流。
但是这显然不正确。有图如下:
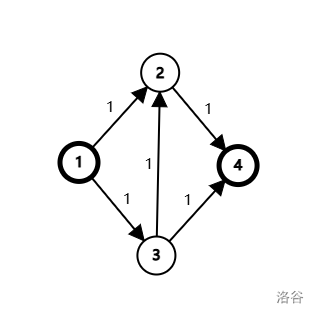
有源点为 \(1\),汇点为 \(4\) 的网络。如果我们一开始就沿着路径 \(1 \to 3 \to 2 \to 4\) 流的话,边 \(2\to 4\) 和 \(1 \to 3\) 的容量被消耗完,不能再流,求得答案为 \(1\)。
但是我们可以沿着路径 \(1 \to 2 \to 4\) 和 \(1 \to 3 \to 4\) 流,答案为 \(2\)。
这说明直接贪心是错误的。
我们考虑反悔贪心。
我们引入【退流】操作。对于每条边,建立反向边,初始容量为 \(0\)。
当一条边(也可以是某条正向边的反向边)被流经时,若流了 \(f\),那么该边剩余容量减 \(f\),该边的反向边剩余容量加 \(f\)。剩下的交给正常贪心。
这样,我们就可以以【错误】的贪心顺序求得正确的答案。
我们考虑这样的图(来自 OI Wiki):
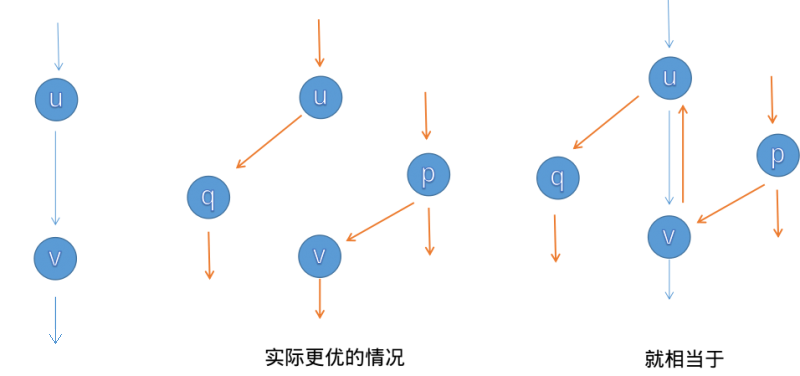
专家发现【退流】操作相当于反悔。这样做是对的。
如果直接这样做,时间复杂度如何?
我们先给出几个定义:
- 剩余容量:一条边的容量减去实际流量。
- 增广路:一条从 \(s\) 到 \(t\) 的路径,路径上边的剩余容量最小值大于 \(0\),即对答案有贡献。
- 残量网络:当前的图中,所有剩余容量大于 \(0\) 的边(包括正向边和反向边)和所有点的集合。
记 \(|V| = n,|E|=m\)。
每轮增广的时间复杂度显然是 \(O(m)\) 的。计算时间复杂度只需要算出增广轮数即可。
极端情况下,有图:
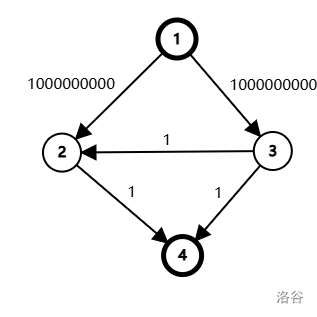
可能以 \(1 \to 3 \to 2 \to 4\) 和 \(1 \to 2 \to 3 \to 4\) 两条路径反复增广约 \(2 \times 10 ^9\) 次。
总复杂度是和值域 \(F\) 有关的,可能还要挂上一个 \(n\) 或 \(m\)。总时间复杂度不敢想象,可能是 \(O(nmF)\) 的。
于是要优化。
Edmonds-Karp 算法
我们考虑用 BFS 实现 FF 方法。具体地,每轮用 BFS 搜出一条增广路,并将其加入答案。每轮 BFS 的时间复杂度是 \(O(m)\) 的,专家可以证明总的增广轮数是不超过 \(O(nm)\) 的,于是总复杂度 \(O(nm^2)\)。
Dinic 算法
我们专家思考 EK 算法的瓶颈。增广时,BFS 是乱搜的,如果我们以一定的顺序增广,可能获得更优的时间复杂度。
在增广前用一遍 BFS 建出(无需显式)最短路径图(即以 \(s\) 至每个结点的 \(dis\) 为键值分层,只保留是最短路径边的图)。我们在最短路径图上增广,每次(一般)用 DFS 搜出一个增广路,更新即可。
有两个优化需要注意:
- 当前弧优化:每次我们维护搜到结点 \(u\) 的出边表中第一条【值得尝试】的边 \(cur_u\)。【值得尝试】指该边的剩余容量大于 \(0\),且它没有被增广路走过(如果走过,那么它的下游仍没有机会增广)。这是保证 Dinic 复杂度的优化,让其不退化至 \(O(nm^2)\)(?)。
值得一提的是,我们的 \(cur\) 指针必须要指向第一个值得尝试的边,不能指向第二条或更后,否则复杂度会假。常见的错误是判 \(sum\) 写错位置,一定要在 \(cur\) 更新前判断。 - 多路增广:我们在一轮增广时,可以不仅搜出一条增广路,可以在某处寻找一个岔路进行继续增广,不立即从头再来。这是 Dinic 的第一个常数优化。
总时间复杂度 \(O(n^2m)\)。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
#define int long long
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 202, M = 5002;
struct Graph {
int n, m, s, t, tot;
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, head[v]), head[v] = tot++;
}
void init() {
cin >> n >> m >> s >> t;
tot = 0;
memset(head, -1, sizeof(head)); //如果tot=0
for(int i = 1, u, v, w; i <= m; ++i) {
cin >> u >> v >> w;
add_edge(u, v, w);
}
}
queue<int> q;
int dis[N];
int BFS() { //在残量网络中打出层次图
for(int i = 1; i <= n; ++i) dis[i] = Linf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e18) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1; //常数优化
}
}
}
return 0;
}
int DFS(int u, int sum = Linf) { //sum:当前流量
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) { //多路增广
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = Linf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while(BFS()) ans += DFS(s);
return ans;
}
} G;
void main() {
G.init();
cout << G.Dinic();
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
例题
二分图最大匹配
我们新建立一个超级源点 \(s\) 和一个超级汇点 \(t\)。对于每个左边点 \(u\),建容量为 \(1\) 的有向边 \((s, u)\)。对于每个右边点 \(v\),建容量为 \(1\) 的有向边 \((v, t)\)。对于左边点 \(u\) 和右边点 \(v\) 之间的(无向)边,建成容量为 \(1\) 的有向边 \((u, v)\)。
这时,跑从 \(s\) 到 \(t\) 的最大流就是二分图的最大匹配。
luogu P3386 【模板】二分图最大匹配
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
#define int long long
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 1005, M = 5e4+5;
struct Graph {
int n, n1, n2, m, s, t, tot;
set<pii> mark;
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, head[v]), head[v] = tot++;
}
void init() {
cin >> n1 >> n2 >> m;
tot = 0;
memset(head, -1, sizeof(head));
for(int i = 1, u, v; i <= m; ++i) {
cin >> u >> v;
if(mark.count(pii(u, v))) continue;
mark.insert(pii(u, v));
add_edge(u, v+n1, 1);
}
s = n1+n2+1, t = n1+n2+2;
for(int i = 1; i <= n1; ++i) add_edge(s, i, 1);
for(int i = n1+1; i <= n1+n2; ++i) add_edge(i, t, 1);
n = n1+n2+2;
}
queue<int> q;
int dis[N];
int BFS() {
for(int i = 1; i <= n; ++i) dis[i] = Linf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e18) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1;
}
}
}
return 0;
}
int DFS(int u, int sum = Linf) {
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) {
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = Linf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while(BFS()) ans += DFS(s);
return ans;
}
} G;
void main() {
G.init();
cout << G.Dinic();
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
如果要输出匹配边,看看哪些左右点之间的边 \((u, v)\) 满流了即可。
luogu P2763 试题库问题
若每个类型要出 \(x\) 道题,那么我们可以将这种类型拆成 \(x\) 个点,对于每个包含这种类型的试题都建点并向这 \(x\) 个点分别连容量为 \(1\) 的有向边。
超级源点连所有试题,所有拆点后的类型连超级汇点,容量均为 \(1\)。
我们发现它实质上就是二分图最大匹配。
输出方案稍微处理一下即可。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 1e6+2, M = 1e6+5;
struct Graph {
int k, n, n1, m, s, t, tot;
vector<int> vec[N];
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, head[v]), head[v] = tot++;
}
void init() {
cin >> k >> n;
n1 = n;
tot = 0, memset(head, -1, sizeof(head));
for(int i = 1, x; i <= k; ++i) {
cin >> x;
for(int j = m+1; j <= m+x; ++j) vec[i].push_back(j);
m += x;
}
for(int i = 1, p; i <= n; ++i) {
cin >> p;
for(int j = 1, x; j <= p; ++j) {
cin >> x;
for(auto ele : vec[x]) add_edge(i, ele + n, 1);
}
}
s = n+m+1, t = n+m+2;
for(int i = 1; i <= n; ++i) add_edge(s, i, 1);
for(int i = n+1; i <= n+m; ++i) add_edge(i, t, 1);
n += m+2;
}
queue<int> q;
int dis[N];
int BFS() {
for(int i = 1; i <= n; ++i) dis[i] = inf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e9) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1;
}
}
}
return 0;
}
int DFS(int u, int sum = inf) {
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) {
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = inf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while(BFS()) ans += DFS(s);
return ans;
}
vector<int> ans[N];
void solve() {
int x = Dinic();
if(x < m) return puts("No Solution!"), void();
for(int i = 1; i <= n1; ++i)
for(int j = head[i]; ~j; j = e[j].next)
if(e[j].v != s && e[j].w == 0) ans[e[j].v].push_back(i);
for(int i = 1; i <= k; ++i) {
cout << i << ": ";
for(auto j : vec[i])
for(auto ele : ans[j + n1]) cout << ele << ' ';
puts("");
}
}
} G;
void main() {
G.init();
G.solve();
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
luogu P3425 [POI 2005] KOS-Dicing
我们将源点 \(s\) 连向每个游戏,容量为 \(1\),每次游戏连向参加的两个人,容量为 \(1\),表示每个游戏只有一个胜者。每个人连向汇点 \(t\),但是容量是多少呢?
我们思考这个容量的实际意义。该边的实际意义就是每个人最多有几个胜场。又注意到题目要求最大值最小,故考虑二分这个容量 \(mid\)。
至于 check 怎么写,只需要看看最大流是不是(大于等于)等于总游戏次数 \(m\)。(最大流的上限就是 \(m\),因为 \(s\) 总共才向外连了 \(m\) 条容量为 \(1\) 的边)
输出方案也很简单,看看每个比赛连哪个人的边满流即可。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 2e4+5, M = 4e4+5;
struct game {
int u, v, w;
game() { }
game(int u, int v) : u(u), v(v) { }
} a[M];
int n, m;
struct Graph {
int n, m, s, t, tot;
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, head[v]), head[v] = tot++;
}
void init(int n, int m, int l) {
this->m = m;
s = n+m+1, t = n+m+2;
tot = 0, memset(head, -1, sizeof(head));
for(int i = 1; i <= m; ++i) {
add_edge(s, i, 1);
add_edge(i, a[i].u + m, 1), add_edge(i, a[i].v + m, 1);
}
for(int i = 1; i <= n; ++i) add_edge(i + m, t, l);
this->n = n+m+2;
}
queue<int> q;
int dis[N];
int BFS() { //在残量网络中打出层次图
for(int i = 1; i <= n; ++i) dis[i] = inf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e9) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1;
}
}
}
return 0;
}
int DFS(int u, int sum = inf) {
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) {
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = inf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic(int op = 0) {
int ans = 0;
while(BFS()) ans += DFS(s);
if(op) {
for(int i = 1; i <= m; ++i)
cout << (e[head[i]].v == a[i].u ^ e[head[i]].w == 1) << '\n';
}
return ans;
}
} G;
bool check(int l) {
G.init(n, m, l);
return G.Dinic() == m;
}
void print(int l) { G.init(n, m, l), G.Dinic(1); }
void main() {
cin >> n >> m;
for(int i = 1; i <= m; ++i) cin >> a[i].u >> a[i].v;
int L = 1, R = n;
while(L < R) {
int mid = L + R >> 1;
if(check(mid)) R = mid;
else L = mid+1;
}
cout << L << '\n';
print(L);
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
luogu P2766 最长不下降子序列问题
第一问是 naive 的 DP,设 \(f_i\) 为 \(a_i\) 结尾的 LIS 即可。
第二问我们考虑怎么建图。所谓【取出】即【不相交】,有点类似匹配。
记 LIS 的长度为 \(mx\)。
我们将源点 \(s\) 向每个 \(f\) 值为 \(1\) 的点连边,将每个 \(f\) 值为 \(mx\) 的点向汇点 \(t\) 连边,每个点向 \(f\) 值比其大 \(1\) 、编号在其后、\(a\) 值不比其小的点连边,容量均为 \(1\),描述 DP 的状态转移过程。
输出最大流即可。
这么连边显然是正确的,每一条 \(s\) 至 \(t\) 的路径就表示一个【取出】的 LIS。由于容量的限制,每个点只会取一次。
第三问只需要在第二问的基础上把 \(s\) 至 \(1\) 号点的边容量改为 \(\infty\),\(n\) 号点至 \(t\) 的边容量改为 \(\infty\) 即可(如果有边)。
注意这一问要特判 \(n=1\) 的情况,输出 \(1\)。但是输出无穷大也有道理?
混合图欧拉回路判定
即,混合图中的无向边定向之后有欧拉回路。
定向之后判断是很容易的,即每个点的入度都等于度数 \(d_i\) 的一半。
考虑用 flow 刻画定向的过程。
原图中边集中的元素 \(e_i=(u_i, v_i)\) 抽象成二分图的左部点,点集中元素抽象成右部点。
定向相当于,源点 \(s\) 向 \(e_i\) 连容量为 \(1\) 的边,卡流量!
\(e_i\) 向 \(u_i\) 和 \(v_i\) 连边,意义是提供入度(无向就连两个,有向就连一个)。
右部点向汇点连边,容量为 \(d_i/2\)。
判定就是是否满流。
DAG 最小路径覆盖
用最少的路径(不在点和边处相交)覆盖全图。
相当于找尽可能多的点有前驱。
每个点的前驱不能相同!想到拆点。拆成 \(u, u'\)。
然后对于原图中的 \((u, v)\),在新的图上连边 \(u\to v'\)。
发现最多有前驱的点的个数就是这个二分图的最大匹配。
于是最小路径覆盖等于 \(n\) 减去二分图最大匹配。
构造就按照匹配来。
问题:如果允许一个点被覆盖多次呢?
这个问题里,默认 \(n,m\) 同阶。
也就是,一条路径可以在中间断开。
一种很唐的思路是,跑一遍传递闭包,然后做上面的过程。
但这时候边数是 \(O(n^2)\) 级别的。太大。
然后看看传递闭包到底慢在哪。
它把一个 \(O(m)\) 能描述的结构扩成了 \(O(n^2)\) 的结构。
仍然拆点。对于每一条边,考虑这样一个结构:
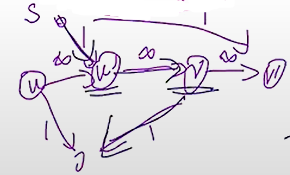
在它上面跑 flow。
这时候一个增广路的含义就相当于二分图的一条匹配边(设为 \(s\to v_1\to v_2\to\dots\to v_k\to t\),那么相当于匹配上了 \(v_1\to v_k\))!并且自动涵盖了可达关系。
构造不会。咕咕咕。(参见习题 [QOJ 6239](https://qoj.ac/problem/6329)
套路
- 转化成二分图匹配,或类似问题。
- 保证一个点只经过一次,可以拆点。
最小割
概念
- 割:一个源点为 \(s\),汇点为 \(t\) 的网络 \(G=(V, E)\),将 \(V\) 划分成 \(S\) 和 \(T\) 两部分,其中 \(s \in S,t \in T\)。那么 \(\{S, T\}\) 称为 \(G\) 的一个 \(s-t\) 割。
- 割边:一条边 \((u, v)\),满足 \(u \in S, v \in T\) ,则该边称为割边。
- 割的容量(大小):即所有割边的容量之和。
解法
对于任意图,有最小割等于最大流。
- 输出最小割的割边:我们从 \(s\) 开始 DFS,只走残量网络中的边,能到达的所有结点的集合就是 \(S\)。接下来在原图中枚举每个 \(S\) 中点的出边,到达的点不属于 \(S\) 的就是割边。
- 一定不能直接输出所有满流边,因为有图:

\(1 \to 2 , 2 \to 4\) 都是满流边,显然不对。
- 一定不能直接输出所有满流边,因为有图:
例题
luogu P5934 [清华集训 2012] 最小生成树
我们考虑最小生成树的过程,即 Kruskal。如果从小到大枚举边,当前加过的边构成的图中,\(u, v\) 不连通,那么当前边 \((u, v)\) 才能加进来。
故权为 \(L\) 的边 \((u, v)\) 在最小生成树中充要条件为所有小于 \(L\) 的边构成的“子图”中,\((u, v)\) 不连通。于是割掉最少的边,使该图的 \((u, v)\) 不连通,就是答案。这个明显等价于最小割。
于是我们在【小于 \(L\)】和【大于 \(L\)】的子图中分别跑最小割,相加即可。
Q:相加即是对的呢?
A:因为两个子图的边集没有交集,割掉的边不会有重复。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 3.2e5+2, M = 6.4e6+2;
struct Graph {
int n, s, t, tot;
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, w, head[v]), head[v] = tot++;
}
void init(int n, int s, int t) {
this->n = n, this->s = s, this->t = t;
tot = 0, memset(head, -1, sizeof(head));
}
queue<int> q;
int dis[N];
int BFS() {
for(int i = 1; i <= n; ++i) dis[i] = inf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e9) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1;
}
}
}
return 0;
}
int DFS(int u, int sum = inf) {
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) {
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = inf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while(BFS()) ans += DFS(s);
return ans;
}
} G1, G2;
int n, m;
int u[N], v[N], w[N];
int s, t, L;
void main() {
cin >> n >> m;
for(int i = 1; i <= m; ++i) cin >> u[i] >> v[i] >> w[i];
cin >> s >> t >> L;
G1.init(n, s, t), G2.init(n, s, t);
for(int i = 1; i <= m; ++i) {
if(w[i] < L) G1.add_edge(u[i], v[i], 1);
else if(w[i] > L) G2.add_edge(u[i], v[i], 1);
}
cout << G1.Dinic() + G2.Dinic();
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
Atcoder ABC239G Builder Takahashi
这题的最小割再显然不过了。但是这道题是点权。
有一个拆点的技巧:将每个点分为入点和出点。原图中的边正常连,权值设为 \(\infty\),点权体现在入点至出点的边的边权。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define int long long
#define all(v) v.begin(), v.end()
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 1002, M = 1e6+2;
struct Graph {
int n, m, s, t, tot;
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, head[v]), head[v] = tot++;
}
void init() {
cin >> n >> m;
s = n+1, t = n;
tot = 0;
memset(head, -1, sizeof(head));
for(int i = 1, u, v; i <= m; ++i) {
cin >> u >> v;
add_edge(u+n, v, Linf), add_edge(v+n, u, Linf);
}
for(int i = 1, c; i <= n; ++i) {
cin >> c;
add_edge(i, i+n, c);
}
n *= 2;
}
queue<int> q;
int dis[N];
int BFS() {
for(int i = 1; i <= n; ++i) dis[i] = Linf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e18) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1;
}
}
}
return 0;
}
int DFS(int u, int sum = Linf) {
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) {
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = Linf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while(BFS()) ans += DFS(s);
return ans;
}
vector<int> ans;
int vis[N];
void mark(int u) {
vis[u] = 1;
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(!vis[v] && e[i].w) mark(v);
}
}
void print() {
mark(s);
for(int i = 1; i <= n; ++i)
if(i <= n/2 && vis[i] && !vis[i + n/2]) ans.push_back(i);
cout << ans.size() << '\n';
for(auto i : ans) cout << i << ' ';
}
} G;
void main() {
G.init();
cout << G.Dinic() << '\n';
G.print();
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
luogu P2774 方格取数问题
一个常用的策略是,最大收益等于总收益减去最小损失。
如果直接建无向网格图的话,既不能体现点权,也不能体现相邻不能同时选。
我们考虑如下建图:
记点 \((i, j)\),若 \(2 | (i + j)\),则其为白点。否则为黑点。
我们建出源点 \(s\),连向所有白点,权值为白点的点权;白点连向各自相邻的黑点,权值为 \(\infty\);所有黑点连向汇点 \(t\),权值为黑点的点权。
最小割就是最小损失。
考虑这么做为什么是对的。
显然,因为是最小割,故不可能割掉白点与黑点之间的边。
割掉一条源点与白点之间的边就代表白点不选,黑点同理。
那么得到的最小割,就不存在 \(s\to t\) 的路径,即满足了相邻黑白点不能同时选(画图易知)。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
#define int long long
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 1e4+5, M = 1e6+2;
struct Graph {
int n, m, s, t, tot, sum;
const int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, head[v]), head[v] = tot++;
}
void init() {
cin >> n >> m;
s = n*m+1, t = n*m+2;
tot = 0;
memset(head, -1, sizeof(head));
for(int i = 1; i <= n; ++i)
for(int j = 1, a; j <= m; ++j) {
scanf("%lld", &a), sum += a;
if(i + j & 1) add_edge((i-1) * m + j, t, a);
else {
for(int o = 0; o < 4; ++o) {
int nx = i + dir[o][0], ny = j + dir[o][1];
if(nx < 1 || nx > n || ny < 1 || ny > m) continue;
add_edge((i-1) * m + j, (nx-1) * m + ny, Linf);
}
add_edge(s, (i-1) * m + j, a);
}
}
n = n * m + 2;
}
queue<int> q;
int dis[N];
int BFS() {
for(int i = 1; i <= n; ++i) dis[i] = Linf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e18) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1;
}
}
}
return 0;
}
int DFS(int u, int sum = Linf) {
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) {
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = Linf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while(BFS()) ans += DFS(s);
return ans;
}
int solve() { return sum - Dinic(); }
} G;
void main() {
G.init();
cout << G.solve();
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
luogu P1646 [国家集训队] happiness
仍然考虑最大收益为总收益减去最小损失。原因:我们直接做无法保证邻座同科的额外收益。
对于单人的文理选择,这是一个二者选其一,故我们直接考虑源点向当前点连容量为文科收益的边,当前点向汇点连容量为理科收益的边。
对于邻座同科的额外收益,我们发现:
- 只要两个人有一个人选理科,那么邻座同文科的收益就要割掉。
记这两个人为 \(x, y\)。我们新建一个点 \(u\),用 \(s\) 向 \(u\) 连容量为同是文科的收益,\(u\) 分别向 \(x, y\) 连容量是 \(\infty\) 的边。这样就可以保证上述条件。
同时理科同理,改成向汇点连边。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
#define int long long
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 1e6+2, M = 2e6+2;
struct Graph {
int n, m, s, t, tot, sum;
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, head[v]), head[v] = tot++;
}
void init() {
cin >> n >> m;
int vertices = n * m;
s = ++vertices, t = ++vertices;
tot = 0;
memset(head, -1, sizeof(head));
auto pos = [=] (int i, int j) { return (i-1) * n + j; };
for(int i = 1; i <= n; ++i)
for(int j = 1, x; j <= m; ++j) {
cin >> x, sum += x;
add_edge(s, pos(i, j), x);
}
for(int i = 1; i <= n; ++i)
for(int j = 1, x; j <= m; ++j) {
cin >> x, sum += x;
add_edge(pos(i, j), t, x);
}
for(int i = 1; i < n; ++i)
for(int j = 1, x; j <= m; ++j) {
cin >> x, sum += x;
add_edge(s, ++vertices, x);
add_edge(vertices, pos(i, j), inf);
add_edge(vertices, pos(i+1, j), inf);
}
for(int i = 1; i < n; ++i)
for(int j = 1, x; j <= m; ++j) {
cin >> x, sum += x;
add_edge(++vertices, t, x);
add_edge(pos(i, j), vertices, inf);
add_edge(pos(i+1, j), vertices, inf);
}
for(int i = 1; i <= n; ++i)
for(int j = 1, x; j < m; ++j) {
cin >> x, sum += x;
add_edge(s, ++vertices, x);
add_edge(vertices, pos(i, j), inf);
add_edge(vertices, pos(i, j+1), inf);
}
for(int i = 1; i <= n; ++i)
for(int j = 1, x; j < m; ++j) {
cin >> x, sum += x;
add_edge(++vertices, t, x);
add_edge(pos(i, j), vertices, inf);
add_edge(pos(i, j+1), vertices, inf);
}
n = vertices;
}
queue<int> q;
int dis[N];
int BFS() {
for(int i = 1; i <= n; ++i) dis[i] = Linf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e18) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1;
}
}
}
return 0;
}
int DFS(int u, int sum = Linf) {
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) {
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = Linf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while(BFS()) ans += DFS(s);
return ans;
}
int solve() { return sum - Dinic(); }
} G;
void main() {
G.init();
cout << G.solve();
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
luogu P2762 太空飞行计划问题
本题仍然有【一个实验所需的仪器集合中有一个不用,那么实验的收益要割掉】的模型。
源点连向实验,代表实验的收益;实验连向仪器,表示依赖关系;仪器连向汇点,不割表示不选,割掉表示选。
总收益减最小割就是答案。
注意读入和方案构造。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
#define int long long
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 2002, M = 50002;
struct Graph {
int n, n0, m, s, t, tot, sum;
int head[N], cur[N];
struct edge {
int v, w, next;
edge() { }
edge(int a, int b, int c) : v(a), w(b), next(c) { }
} e[M << 1];
void add_edge(int u, int v, int w) {
e[tot] = edge(v, w, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, head[v]), head[v] = tot++;
}
void readtools(int i) {
char tools[10000];
memset(tools, 0, sizeof(tools));
cin.getline(tools, 10000);
int ulen = 0, tool;
while(sscanf(tools + ulen, "%lld", &tool) == 1) {
add_edge(i, tool + n, Linf);
if(tool == 0) ++ulen;
else while(tool) {
tool /= 10;
++ulen;
}
++ulen;
}
}
void init() {
cin >> n >> m;
s = n + m + 1, t = n + m + 2;
tot = 0, memset(head, -1, sizeof(head));
for(int i = 1, v; i <= n; ++i) {
scanf("%lld", &v), add_edge(s, i, v), sum += v;
readtools(i);
}
for(int i = 1, price; i <= m; ++i) {
cin >> price;
add_edge(i + n, t, price);
}
n0 = n;
n += m + 2;
}
queue<int> q;
int dis[N];
int BFS() {
for(int i = 1; i <= n; ++i) dis[i] = Linf, cur[i] = head[i];
queue<int>().swap(q);
q.push(s);
dis[s] = 0;
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v;
if(e[i].w > 0 && dis[v] > 1e18) {
q.push(v);
dis[v] = dis[u] + 1;
if(v == t) return 1;
}
}
}
return 0;
}
int DFS(int u, int sum = Linf) {
if(u == t) return sum;
int res = 0;
for(int i = cur[u]; ~i && sum > 0; i = e[i].next) {
cur[u] = i;
int v = e[i].v;
if(e[i].w > 0 && dis[v] == dis[u] + 1) {
int k = DFS(v, min(sum, e[i].w));
if(k == 0) dis[v] = Linf;
e[i].w -= k, e[i ^ 1].w += k;
res += k, sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while(BFS()) ans += DFS(s);
return ans;
}
void solve() {
int ans = sum - Dinic();
for(int i = 1; i <= n0; ++i)
if(dis[i] < 1e18) cout << i << ' ';
cout << '\n';
for(int i = n0+1; i <= n0+m; ++i)
if(dis[i] < 1e18) cout << i - n0 << ' ';
cout << '\n' << ans << '\n';
}
} G;
void main() {
G.init();
G.solve();
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
套路
- 看似是最大流但是不可做的题目,可以将最大收益转化成总收益减最小损失,用最小割建图处理。
- 上下一定的依赖关系,可以有【下面有一个不选,上面的收益就要割掉】的建图。
- 点权可以拆点转化成边权。
费用流
概念
网络的边不仅有容量,还有一个费用 \(cost\),表示 \(1\) 单位流过所需费用。
我们主要研究最小费用最大流(Minimum Cost Maximum Flow),即在最大流的基础上费用要最小。最大费用最大流同理。
解法
以下陈述 MCMF 的解法。
我们在 Dinic 求最大流的时候,用 BFS 将当前残量网络处理出层次图,沿着最短路的更新方向增广。
现在我们需要在保证最大流的基础上,让费用最小。我们自然地想到用亖了的 SPFA 或 Bellman-Ford 处理出残量网络中 \(cost\) 的最短路层次图。
专家可以证明这是对的。
但是要注意,该算法不能用于求解 \(cost\) 有负环的网络,有负环时还需消圈。
Q:为什么要用 SPFA?
A:即使原图中 \(cost\) 没有负权边,但是建反边的时候要将 \(cost\) 赋为正边的相反数,以达到【退流】中反悔的目的。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
#define int long long
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 5e3+2, M = 5e4+2;
template<class T1, class T2>
pair<T1, T2> operator + (pair<T1, T2> a, pair<T1, T2> b) { return pii(a.first + b.first, a.second + b.second); }
struct Graph {
int n, m, s, t;
int head[N], tot, cur[N];
struct edge {
int v, w, cost, next;
edge() { }
edge(int a, int b, int c, int d) : v(a), w(b), cost(c), next(d) { }
} e[M << 1];
void add_edge(int u, int v, int w, int cost) {
e[tot] = edge(v, w, cost, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, -cost, head[v]), head[v] = tot++;
}
void init() {
cin >> n >> m >> s >> t;
tot = 0, memset(head, -1, sizeof(head));
for(int i = 1, u, v, w, cost; i <= m; ++i) {
scanf("%lld%lld%lld%lld", &u, &v, &w, &cost);
add_edge(u, v, w, cost);
}
}
int dis[N], exist[N], vis[N];
queue<int> q;
bool SPFA() {
for(int i = 1; i <= n; ++i) dis[i] = Linf, exist[i] = 0, cur[i] = head[i], vis[i] = 0;
dis[s] = 0, exist[s] = 1;
queue<int>().swap(q);
q.push(s);
while(!q.empty()) {
int u = q.front(); q.pop();
exist[u] = 0;
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v, cost = e[i].cost;
if(e[i].w > 0 && dis[u] + cost < dis[v]) {
dis[v] = dis[u] + cost;
if(!exist[v]) exist[v] = 1, q.push(v);
}
}
}
return dis[t] < 1e18;
}
pii DFS(int u, int sum = Linf) {
if(u == t) return pii(sum, 0);
vis[u] = 1;
int res = 0, c = 0;
for(int i = cur[u]; ~i; i = cur[u] = e[i].next) {
int v = e[i].v, cost = e[i].cost;
if(vis[v]) continue; //防止零环让 DFS 反复更新
if(e[i].w > 0 && dis[v] == dis[u] + cost) {
auto [a, b] = DFS(v, min(sum, e[i].w));
if(a == 0) dis[v] = Linf;
e[i].w -= a, e[i ^ 1].w += a;
res += a, c += a * cost + b, sum -= a;
if(sum == 0) break;
}
}
return pii(res, c);
}
pii Dinic() {
pii ans = pii(0, 0);
while(SPFA()) ans = ans + DFS(s);
return ans;
}
} G;
void main() {
G.init();
pii ans = G.Dinic();
cout << ans.first << ' ' << ans.second;
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
最大费用最大流,将所有边的费用改为相反数,跑最小费用最大流之后费用取负即可。(前提是原图没有正环)
例题
luogu P4013 数字梯形问题
一堆路径从上面流到下面,一看就很最大流。
但是容量是什么呢?
我们发现,容量只能用来限制题目中的条件。于是,就可以考虑引入费用,计算最大收益。
对于第一问,每个【点】只能经过一次。经典地,将一个点拆成两个,中间连上容量为 \(1\),费用为点权的边,称为点内边。
对于第二问,每条【边】只能经过一次。我们将第一问的点内边的容量改为 \(\infty\),且最后一排点连到汇点的边的容量改为 \(\infty\) 即可。
对于第三问,除了源点连向第一排点的边,其他边容量全是 \(\infty\)。
跑最大费用最大流即可。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
#define int long long
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 1402, M = 14002;
template<class T1, class T2>
pair<T1, T2> operator + (pair<T1, T2> a, pair<T1, T2> b) { return pii(a.first + b.first, a.second + b.second); }
int n, m, a[42][42], pos[42][42], idx;
struct Graph {
int n, m, s, t;
int head[N], tot, cur[N];
struct edge {
int v, w, cost, next;
edge() { }
edge(int a, int b, int c, int d) : v(a), w(b), cost(c), next(d) { }
} e[M << 1];
void add_edge(int u, int v, int w, int cost) {
e[tot] = edge(v, w, cost, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, -cost, head[v]), head[v] = tot++;
}
void init(int opt) {
s = 2*idx + 1, t = 2*idx + 2;
n = Traveller::n, m = Traveller::m;
tot = 0, memset(head, -1, sizeof(head));
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m + i - 1; ++j) add_edge(pos[i][j], pos[i][j] + idx, opt == 1 ? 1 : Linf, -a[i][j]);
for(int i = 1; i < n; ++i)
for(int j = 1; j <= m + i - 1; ++j)
add_edge(pos[i][j] + idx, pos[i+1][j], opt <= 2 ? 1 : Linf, 0),
add_edge(pos[i][j] + idx, pos[i+1][j+1], opt <= 2 ? 1 : Linf, 0);
for(int i = 1; i <= m; ++i) add_edge(s, pos[1][i], 1, 0);
for(int i = 1; i <= n + m - 1; ++i) add_edge(pos[n][i] + idx, t, opt == 1 ? 1 : Linf, 0);
n = 2*idx + 2;
}
int dis[N], exist[N], vis[N];
queue<int> q;
bool SPFA() {
for(int i = 1; i <= n; ++i) dis[i] = Linf, exist[i] = 0, cur[i] = head[i], vis[i] = 0;
dis[s] = 0, exist[s] = 1;
queue<int>().swap(q);
q.push(s);
while(!q.empty()) {
int u = q.front(); q.pop();
exist[u] = 0;
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v, cost = e[i].cost;
if(e[i].w > 0 && dis[u] + cost < dis[v]) {
dis[v] = dis[u] + cost;
if(!exist[v]) exist[v] = 1, q.push(v);
}
}
}
return dis[t] < 1e18;
}
pii DFS(int u, int sum = Linf) {
if(u == t) return pii(sum, 0);
vis[u] = 1;
int res = 0, c = 0;
for(int i = cur[u]; ~i; i = cur[u] = e[i].next) {
int v = e[i].v, cost = e[i].cost;
if(vis[v]) continue;
if(e[i].w > 0 && dis[v] == dis[u] + cost) {
auto [a, b] = DFS(v, min(sum, e[i].w));
if(a == 0) dis[v] = Linf;
e[i].w -= a, e[i ^ 1].w += a;
res += a, c += a * cost + b, sum -= a;
if(sum == 0) break;
}
}
return pii(res, c);
}
pii Dinic() {
pii ans = pii(0, 0);
while(SPFA()) ans = ans + DFS(s);
return ans;
}
int solve() { return -Dinic().second; }
} G;
void main() {
cin >> m >> n;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m + i - 1; ++j) cin >> a[i][j];
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m + i - 1; ++j) pos[i][j] = ++idx;
G.init(1), cout << G.solve() << '\n';
G.init(2), cout << G.solve() << '\n';
G.init(3), cout << G.solve() << '\n';
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
luogu P2604 [ZJOI2010] 网络扩容
第一问简单。记算出来的最大流为 \(f\)。
第二问要求将最大流增加 \(k\)。现在的最大流就是 \(f+k\),不能多不能少。
我们可以新建源点 \(s\),向旧源点(\(1\))连一条容量为 \(f+k\),费用为 \(0\) 的边,达到限流目的。
我们将原图中的所有边分为【免费边】和【付费边】。【免费边】即为原来跑出最大流所需的,不用算在扩容费用中;【付费边】容量设为 \(\infty\),表示想扩多少扩多少,但是要付费。跑一遍 MCMF 即可。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define all(v) v.begin(), v.end()
#define int long long
using namespace std;
//#define filename "xxx"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1
namespace Traveller {
const int N = 5e3+2, M = 5e4+2;
template<class T1, class T2>
pair<T1, T2> operator + (pair<T1, T2> a, pair<T1, T2> b) { return pii(a.first + b.first, a.second + b.second); }
struct node {
int a, b, c, d;
node() { }
node(int a, int b, int c, int d) : a(a), b(b), c(c), d(d) { }
};
vector<node> vec;
int ans;
struct Graph {
int n, m, k, s, t;
int head[N], tot, cur[N];
struct edge {
int v, w, cost, next;
edge() { }
edge(int a, int b, int c, int d) : v(a), w(b), cost(c), next(d) { }
} e[M << 1];
void add_edge(int u, int v, int w, int cost) {
e[tot] = edge(v, w, cost, head[u]), head[u] = tot++;
e[tot] = edge(u, 0, -cost, head[v]), head[v] = tot++;
}
void init() {
cin >> n >> m >> k;
s = 1, t = n;
tot = 0, memset(head, -1, sizeof(head));
for(int i = 1, u, v, w, cost; i <= m; ++i) {
scanf("%lld%lld%lld%lld", &u, &v, &w, &cost);
add_edge(u, v, w, 0);
vec.emplace_back(u, v, w, cost);
}
}
void work() {
s = n+1, t = n++;
tot = 0, memset(head, -1, sizeof(head));
add_edge(s, 1, ans+k, 0);
for(auto [u, v, w, cost] : vec)
add_edge(u, v, w, 0), add_edge(u, v, Linf, cost);
}
int dis[N], exist[N], vis[N];
queue<int> q;
bool SPFA() {
for(int i = 1; i <= n; ++i) dis[i] = Linf, exist[i] = 0, cur[i] = head[i], vis[i] = 0;
dis[s] = 0, exist[s] = 1;
queue<int>().swap(q);
q.push(s);
while(!q.empty()) {
int u = q.front(); q.pop();
exist[u] = 0;
for(int i = head[u]; ~i; i = e[i].next) {
int v = e[i].v, cost = e[i].cost;
if(e[i].w > 0 && dis[u] + cost < dis[v]) {
dis[v] = dis[u] + cost;
if(!exist[v]) exist[v] = 1, q.push(v);
}
}
}
return dis[t] < 1e18;
}
pii DFS(int u, int sum = Linf) {
if(u == t) return pii(sum, 0);
vis[u] = 1;
int res = 0, c = 0;
for(int i = cur[u]; ~i && sum > 0; i = cur[u] = e[i].next) {
int v = e[i].v, cost = e[i].cost;
if(vis[v]) continue;
if(e[i].w > 0 && dis[v] == dis[u] + cost) {
auto [a, b] = DFS(v, min(sum, e[i].w));
if(a == 0) dis[v] = Linf;
e[i].w -= a, e[i ^ 1].w += a;
res += a, c += a * cost + b, sum -= a;
}
}
return pii(res, c);
}
pii Dinic() {
pii ans = pii(0, 0);
while(SPFA()) ans = ans + DFS(s);
cerr << '\n';
return ans;
}
} G;
void main() {
G.init();
cout << (ans = G.Dinic().first) << ' ';
G.work();
cout << G.Dinic().second << '\n';
}
}
signed main() {
#ifdef filename
FileOperations();
#endif
signed _ = 1;
#ifdef multi_cases
scanf("%d", &_);
#endif
while(_--) Traveller::main();
return 0;
}
luogu P1251 餐巾计划问题
看起来很傻。源点连向每一天的开头(表示餐巾是干净的,记作 \(i_1\))。每一天结束(表示餐巾是脏的,记作 \(i_2\))连向汇点。容量均为无穷,费用均为 \(p\)。
然后快洗就是 \(i_2 \to (i+m)_1\) 连费用是 \(f\) 的边。
每天的需求量就可以表征为,\(i_1 \to i_2\) 要至少流当天需求量(记为 \(a_i\))的流。这里有点困难。
改造这个图。
将 \(t\) 先连向 \(s\),容量无穷,费用 \(0\)。这样就转化为了一个“上下界最小可行流”。
然后显然不愿意跑这个。原来不是 \(i_1 \to i_2\) 吗,现在改一下,建一个超级源点 \(s'\),一个超级汇点 \(t'\),将上面这条边拆掉,改为 \(i_1 \to t',s'\to i_2\)。容量均为 \(a_i\),费用为 \(0\)。
这样跑 MCMF 就行了。
这样转化“至少边”的妙处在于,最大流一定能满流,满流就一定能达到每天 \(a_i\) 的下界限制。
luogu P3980 志愿者招募
难点仍然是如何控制“至少边”。
解决方法很简单。源点连向第一天,容量为 \(M\)(一个大于总人数的值),费用为 \(0\)。“至少边”套路地转化为保证满流的结构。
具体地,第 \(i\) 天指向第 \(i+1\) 天,第 \(n+1\) 天为汇点。容量为 \(M-a_i\),然后对于所有的 \((s,t,c)\) 限制,将第 \(s\) 天连向第 \(t\) 天,容量为无穷,费用为 \(c\)。这个结构可以保证 \(s\to t\) 这条边满流!
跑 MCMF 即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号