线性回归问题

线性回归问题

Model（fuaction set）

​ 一次模型：y = b + w * x

w 和 b 可以表示任何值，所以说一共有无穷多的function。

线性模型

\[y = b + \sum{w_i*x_i} \]

\[x_i:表示各种输入的值，如身高、体重、cp值等等，统称为feature。 w_i:weight,b:bias \]

方程的好坏

​ 利用Training Data来定义一个方程的好坏。

Loss function L：用于定义一个方程输出的数据的好坏。

\[L(f) = L(w,b) = \sum_{n=1}^{10}{(y^n - (b + w*x_i))^2} \]

\[注意：y^n为真正的数值，而 b +w*x_i则为预测的数值 \]

L（f）为估测误差，L越大表示方程越差。

故要找出L最小的方程！

\[用f^*来表示L最小的方程 \]

Gradient Descent (梯度下降)

前提

只要function可导即可。

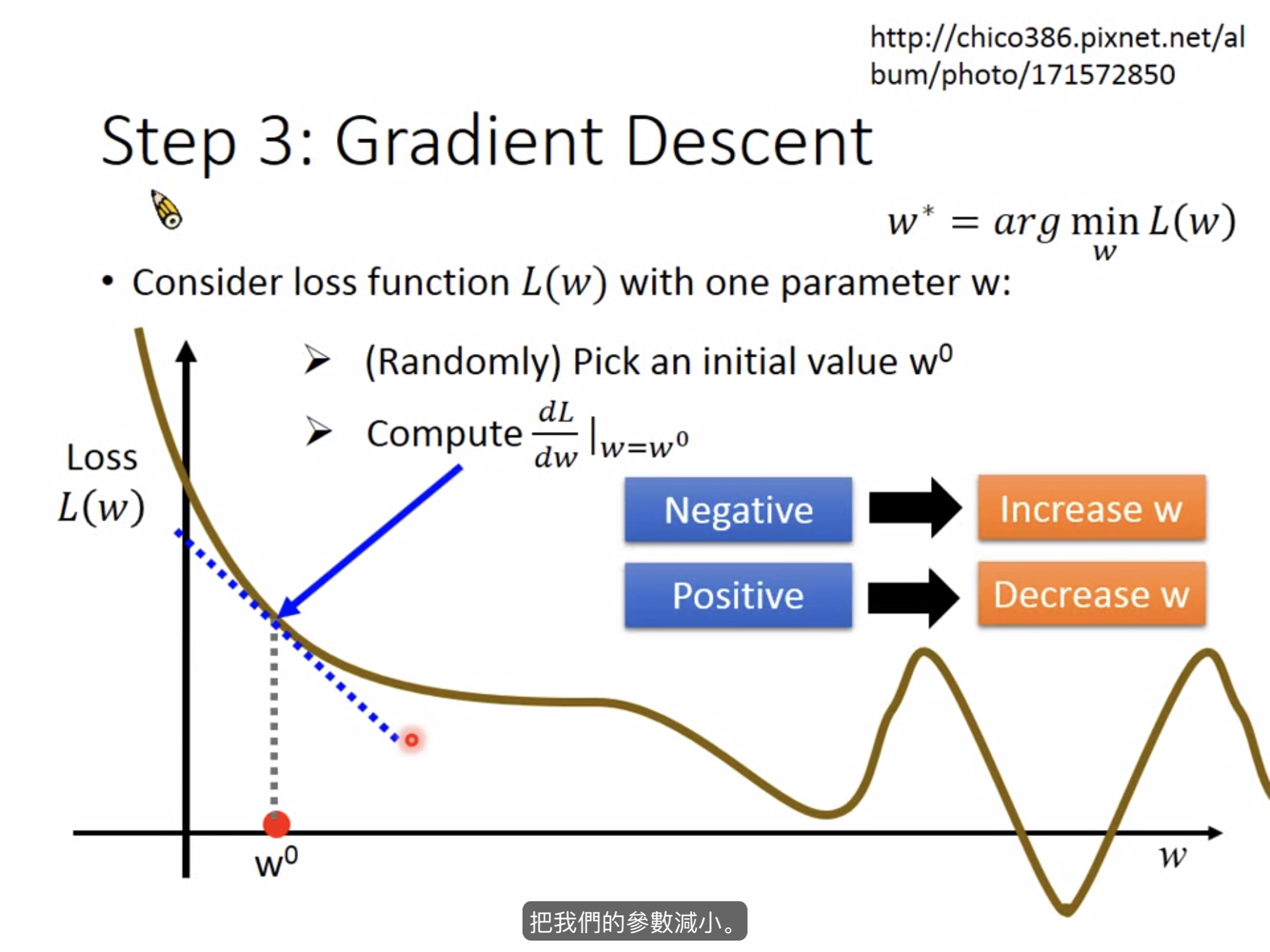
具体做法（一个参数）

1. 随机选取一个点w

2. \[dL/dw|w=w_0 \]

3. 若这个斜率为负的则增加w值，反之则减小w值

4. 微分值越大，表示此时所在的位置越陡峭，要增加或者减小的值越大。

5. \[w_1<——w_0-\eta*dL/dw|w=w_0 \]

6. \[\eta表示学习速率，\eta越大表示参数更新的幅度越大，学习的速度就会比较快。 \]

7. \[w_2<——w_1-\eta*dL/dw|w=w_1 \]

8. 一直持续下去，会找到一个极值点，此时的微分值为0，参数不再更新。

9. 注意⚠️：在线性回归问题上极值点就是最值点，故无需多加考虑，极值点不是最值点的问题

   

具体做法（两个参数）

​ 与一个参数的做法相同，只不过换为求偏导，然后分别移动两个参数的值。

​ 两个参数的学习效率是相同的

\[L(f) = L(w,b) = \sum_{n=1}^{10}{(y^n - (b + w*x_i))^2} \]

\[\frac{\partial L}{\partial w} =2\sum_{n=1}^{10}{(y^n - (b + w*x_i))^2}(-x_i) \]

\[\frac{\partial L}{\partial b} =-2\sum_{n=1}^{10}{(y^n - (b + w*x_i))^2} \]

最好的 b 和 w 是使上述两个偏导为0

​