matlab学习笔记9 随机变量与概率分布以及蒙特卡洛方法

概率分布函数

下图的函数作用是求某点处的B(n,p)的概率，横坐标为实验所得值，即x，从中可见e(x)=12


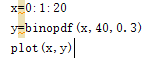
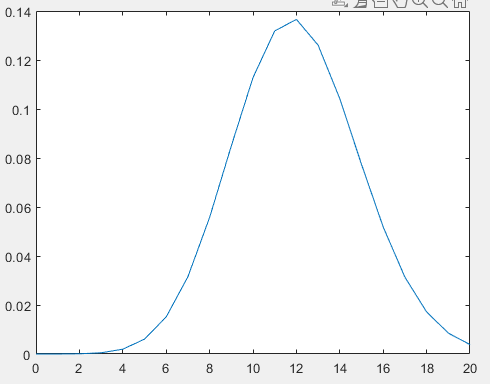
unidpdf(k,N)为均匀分布函数的概率密度在随机范围为1到N的正整数中取k的概率,若需要离散的情况可改用unifpdf

y=unidpdf(1:1:10,20)%unidpdf(k,N)为均匀分布函数的概率密度在随机范围为1到N的正整数中取k的概率,若需要离散的情况可改用unifpdf
y =

  列 1 至 8

    0.0500    0.0500    0.0500    0.0500    0.0500    0.0500    0.0500    0.0500

  列 9 至 10

    0.0500    0.0500

另一个例子,当范围不从0/1开始时，要用两个参数指定范围

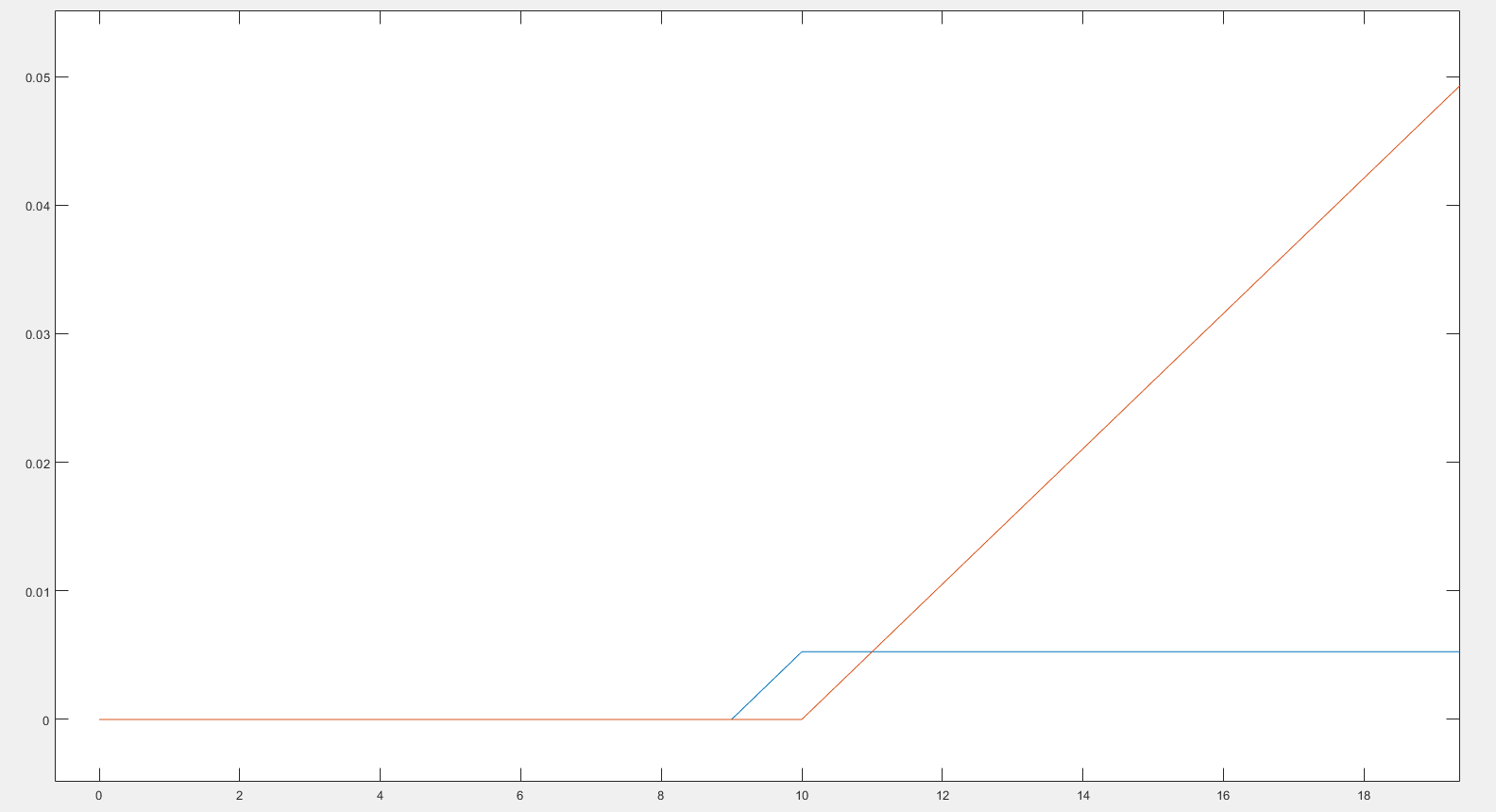
cdf为分布函数,对cdf(x)，值为随机变量<=x的概率


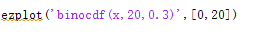
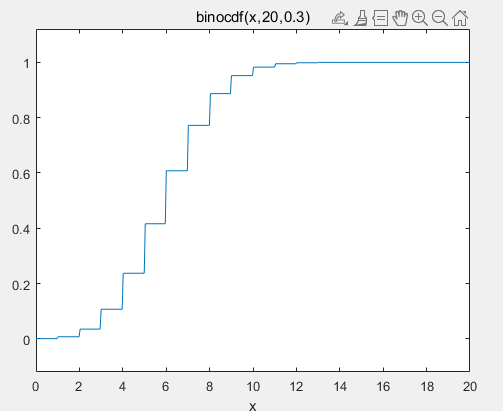
当我们需要P(t1<=x<=t2)时候，可以用cdf(x,t2)-cdf(x,t1)得到

特殊的分布

1. 正态分布

normpdf(x,u,sigma)

2.泊松分布

random('poisson',3,1,10)%生成一个1*10矩阵，每个元素服从Pi（3）分布

生成随机数

注意正态分布使用的是sigma而非其平方，指数分布使用的是其期望本身

怎么得到一个自定义的概率函数的随机值？

注意到自定义的函数F(x)的定义域可能很大，难以直接求，于是想到使用反函数

课堂练习

画出指数分布E（0.1）的概率密度和分布函数

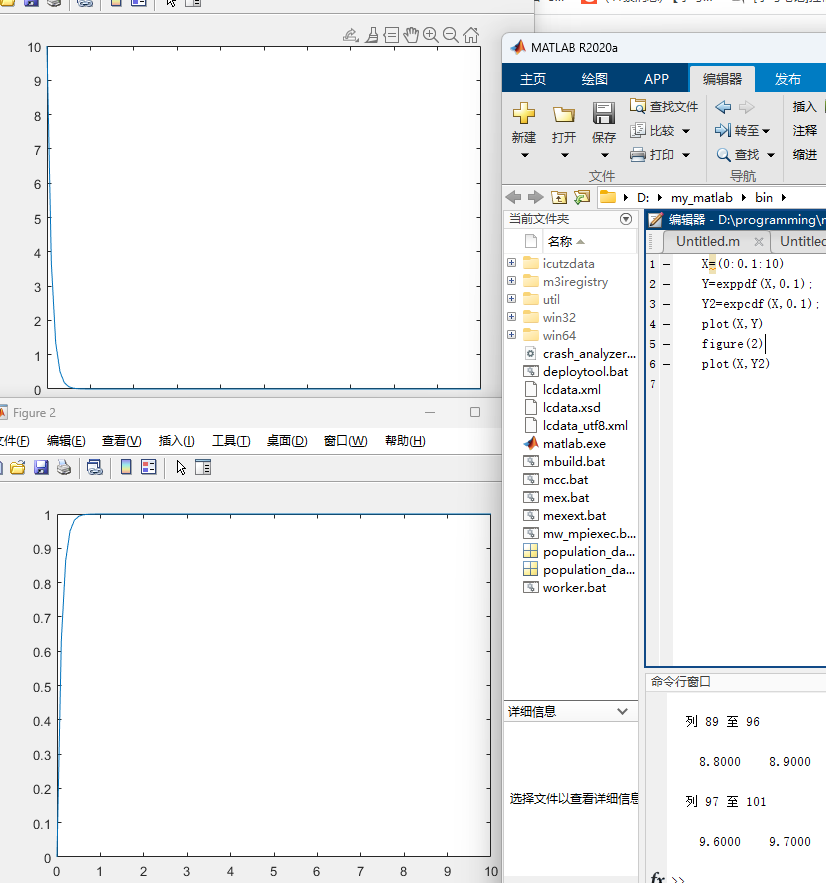
蒙特卡洛

求定积分：

求x.^10.*(2+sin(x))在【0,1】上的积分