matlab学习笔记8关于矩阵和线性代数

从基础的开始

eye(m,n) % 生成单位矩阵
size(A)%返回A的类型
eye(size(A))%生成同型矩阵
rand(m,n) %生成均匀分布矩阵
randn(m,n)%均值为0，方差为1的正态分布矩阵
vander(C)%生成范德蒙德矩阵
diag(v,k)%v是一个向量，k=0时本函数生成一个对角矩阵，主对角线是v，k代表将v从主对角线左移或右移k列再作为对角线生成，由于这个性质，生成的矩阵的size并不确定，取决于向量长度和位置
compan(p)%生成p的伴随矩阵

p=[a0,a1,a2....an]=\(a_0*x^n+a_1*x^(n-1)+...+a_n\)

高级一点的

有时我们不想要数值近似解，此时可以考虑转符号类型

A=[sin(pi/4),1]
B=sym(A)%输出A和B即可看到差别
tril(A,k)取第k条对角线往下的元素
triu(A,k)取第k条对角线往上的元素
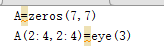
A=[B;C D]% A是上面为A和零矩阵，下面为C D的大扩充矩阵
A(1,:)=[]%删除第一行

在指明了位置的情况下可以直接赋值

多项式

p=poly2sym(p) //p=[1,2,3,4,5] 得到p=x^4+2x^3+3x^2+4x+5
polyval(p,a) //return p(x)'value when x=a
roots(p)// return all roots of the polynomial p refers to
[x,y]=conv(p1,p2)//return the result of multiplying p1 p2 
//the explanation of function deconv is below, remember b is the numerator of the remind polonominal

examples

p=[1,2,3,4]
polyval(p,2)%得26

p=[1,2,1]
roots(p) %ans=-1

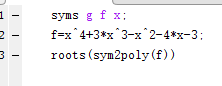
syms f y;
f=(y-1)*(y^2-y-1);
expand(f)
% ans =
% y^3 - 2*y^2 + 1

一种对隐式符号变量画图的简单办法



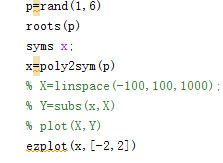
分解为最简分式 a是分子多项式系数 b是所有形如x-a的分母的常数项a c是余项

线性方程组

null(A,'r')%得到系数矩阵A的基础解系 加参数r使结果变成有理解
//下面求非齐次方程组的解
x0=pinv(A)*b
x0=A\b
//求特征值和特征向量
A=[4 6 0;-3 -5 0;-3 -6 5]
[V D]=eig(A)
//阶乘
factorial(n)