牛客网Grid Coloring

链接：https://ac.nowcoder.com/acm/contest/5671/G
来源：牛客网

题目描述：

Roundgod draws a grid graph of size nnn with n×nn \times nn×n cells. She can use one of kkk colors to color every edge once, but lzr gives her some limits.

1. lzr loves balance. All colors should appear in the same number of times.
2. lzr loves complexity. The graph should not contain any monochromatic cycle.
3. lzr hates monotone. Each whole horizontal or vertical line of the graph should contain at least two colors

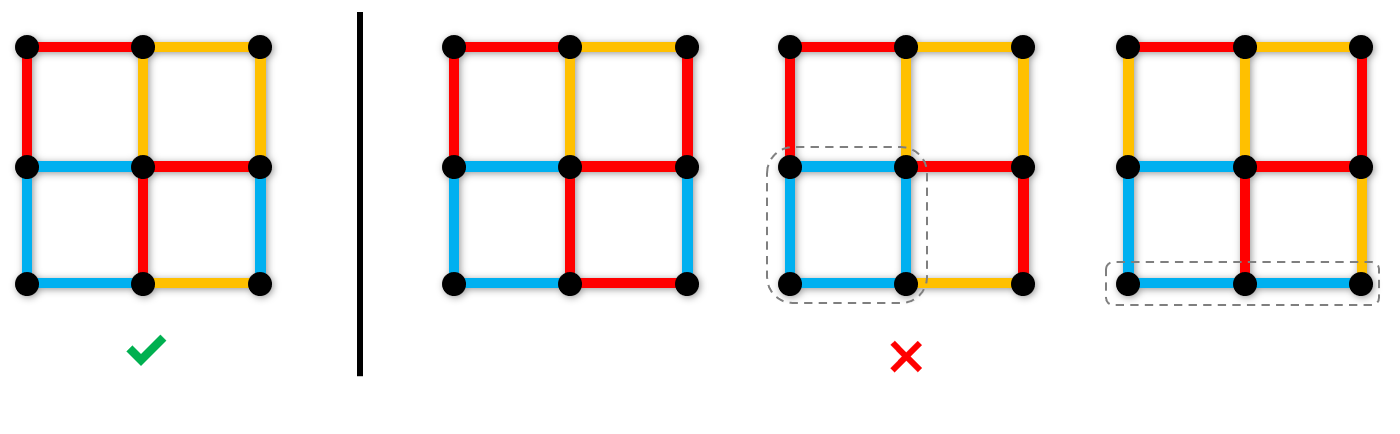
Roundgod is so divine that she doesn't want to waste her god's power to solve this problem. Could you give her a solution?

输入描述:

The input contains multiple test cases. The first line of input contains one integer T (1≤T≤100)T\ (1\le T\le100)T (1≤T≤100).
In the following TTT lines, each line contains two integers n,k (1≤n≤200,1≤k≤2(n+1)n)n,k\ (1\le n\le200,1\le k\le2(n+1)n)n,k (1≤n≤200,1≤k≤2(n+1)n) describing one test case.

输出描述:

For each test case, if there's no solution, please output "-1".

Otherwise, output 2(n+1)2(n+1)2(n+1) lines.

For the first n+1n+1n+1 lines, each line contains nnn integers, denoting colors of edges on every horizontal line.

For the last n+1n+1n+1 lines, each line contain nnn integers, denoting colors of edges on every vertical line.

 

 

翻译自行解决。

分析：

构造题。

首先判断是否存在构造。当n=1n=1时，不能满足条件3，当k=1k=1时，不能满足条件2和3，当(2∗n∗(n+1))modk≠0(2∗n∗(n+1))modk≠0时，不能满足条件1。对以上三种情况进行特判，输出−1−1。

然后将行和列提取出来，将行构成一个(n+1)∗n(n+1)∗n的表，将列构成一个n∗(n+1)n∗(n+1)的表。

对于奇偶不同的nn，分类讨论即可。

 

下方代码

 

 

 

#include<bits/stdc++.h>
using namespace std;
int l;
int n,k,t;
int a[210][210];
int b[210][210];
int main()
{
    scanf("%d",&l);
    while(l--)
    {
        scanf("%d%d",&n,&k);
        if (n==1 || k==1 || (2*n*(n+1))%k)
        {
            printf("-1\n");
            continue;
        }
        t=0;
        for (int i=0; i<n; i++)
        {
            for (int j=0; j<n; j++)
            {
                t=t%k+1;
                a[i][j]=t;
            }
            for (int j=0; j<=n; j++)
            {
                t=t%k+1;
                b[j][i]=t;
            }
        }
        for (int i=0; i<n; i++)
        {
            t=t%k+1;
            a[n][i]=t;
        }
        for(int i=0; i<=n; i++)
        {
            for(int j=0; j<n; j++)
                printf("%d ",a[i][j]);
            cout<<endl;
        }
        for(int i=0; i<=n; i++)
        {
            for(int j=0; j<n; j++)
                printf("%d ",b[i][j]);
            cout<<endl;
        }
    }
    return 0;
}