CF1654D - Potion Brewing Class(搜索技术 + 数学规律 + 数论 + 树 / *2100)
1654D - Potion Brewing Class(源地址自⇔CF1654D)
tag
⇔搜索技术、⇔数学规律、⇔数论、⇔树、⇔*2100
题意
给定 \(N\) 种原材料和 \(N-1\) 条配方比(每条配方比 \(i,j,p,q\) 代表原料 \(i\) 和 \(j\) 的比例为 \(p:q\) ),规定用量必须为整数,你需要找到每种材料最小的用量,输出总用量的最小值。
\(1 \le T \le 10^4\) 组样例,满足 \(2≤N≤2*10^5,1≤i,j≤n, i≠j,1≤p,q≤n\) 。保证答案唯一。
思路
由题意可知,可以构建出一棵树。
\(N\) 个点和 \(N-1\) 条边,保证是树;答案唯一,保证是一棵树。
赛时思路(是错的)
点击查看原因
根据前两个样例的模拟,我发现,我们只需要直接做一遍 \(\tt{}DFS\) ,找到比值最大的那个点,那么由于它的比值是最大的,它的值就可以被确定,只需要以这个点为根再做一遍 \(\tt{}DFS\) 即可确定剩下的全部点(别骂,赛时我真的觉得这个方法完美QWQ)。然而我写完了之后测第三个样例才意识到,这道题需要取模,而取模之后是无法比较大小的,然后我就陷入了迷茫……
在写这一篇题解的时候我又复盘思考了很久,当时的思路,第一遍 \(\tt{}DFS\) 确实是可行的(如果能解决比较大小的问题),而错误的地方在于第二遍 \(\tt{}DFS\) 的过程——更新完根节点的所有子节点后,下一步应该怎么做?按照赛时的思路,我使用优先队列储存点值,每次取出值最大的点作为新的根节点,并更新其子节点(思路源于堆优化版 \(\tt{}Djikstra\) )。而问题在就于无法找到剩余值最大的点——上一层只更新了部分节点。至此,算法退化至 \(\mathcal{O}(N^2)\) ,宣告死亡。
附赛时代码,代码中存在以下问题未被解决:
- 第一遍 \(\tt{}DFS\) 前得到的值并不是最优的(这就导致我尝试在最后加上一行 \(\tt{}\_\_gcd\) 进行优化);
- 未处理取模后比较大小的问题;
- 如上所述,致命缺陷。
点击查看代码
//====================
const int N = 1e6 + 7;
int n, a[N];
vector<PIII> ver[N];
int v[N];
VI ans;
//====================
void Solve()
{
cin >> n;
FOR (i, 1, n) {
v[i] = 0, a[i] = 1, ver[i].clear();
}
ans.clear();
FOR (i, 1, n - 1) {
int x, y, w1, w2; cin >> x >> y >> w1 >> w2;
ver[x].pb({y, w1, w2}), ver[y].pb({x, w2, w1});
int t = mygcd(w1, w2);
w1 /= t, w2 /= t;
int W1 = a[x], W2 = a[y];
a[x] *= w1 * W2, a[y] *= w2 * W1;
}
int m = 0, mnum = 0;
FOR (i, 1, n) {
if (a[i] > m) {
m = a[i];
mnum = i;
}
}
priority_queue<PII> q; q.push({m, mnum});
while (!q.empty()) {
auto [w, x] = q.top(); q.pop();
ans.pb(w);
v[x] = 1;
for (auto [y, w1, w2] : ver[x]) {
if (v[y]) continue;
a[y] = max(a[y], w / w1 * w2);
}
m = 0, mnum = 0;
for (int i = 1; i <= n; ++ i) {
if (a[i] > m && v[i] == 0) {
m = a[i];
mnum = i;
}
}
if (mnum != 0) q.push({m, mnum});
}
int num = ans[0];
Z Ans = ans[0];
FOR (i, 1, n - 1) {
num = __gcd(num, ans[i]);
Ans += ans[i];
}
Ans /= num;
cout << Ans.val() << endl;
}
正解
我们从逆向的角度出发思考本题。假定用量可以是分数:不妨设 \(1\) 号原料的用量为 \(1\) ,那么通过一遍 \(\tt{}DFS\) 可以得到其他所有原料的用量,而转化分数为整数的方式也很简单,如果我们能找到一个整数 \(T\) ,使得所有的数乘上 \(T\) 后都能变成整数,那么就可以解决分数的问题。
现在,问题变成了如何求解 \(T\) ,假定不考虑最小值:答案即为 \(\tt{}lcm(p_1,p_2,…)\) ,而我们发现,如果 \(p\) 中的某一些因子在此前的 \(q\) 中出现过,那么就不需要再加入计算了,所以,我们要维护一个 \(\tt{}size\) 数组用于统计此前场上出现过的因子数量,以及一个 \(\tt{}max\_size\) 数组用于统计某一个因子此前出现过的最大数量。
以样例2举例说明,如下。
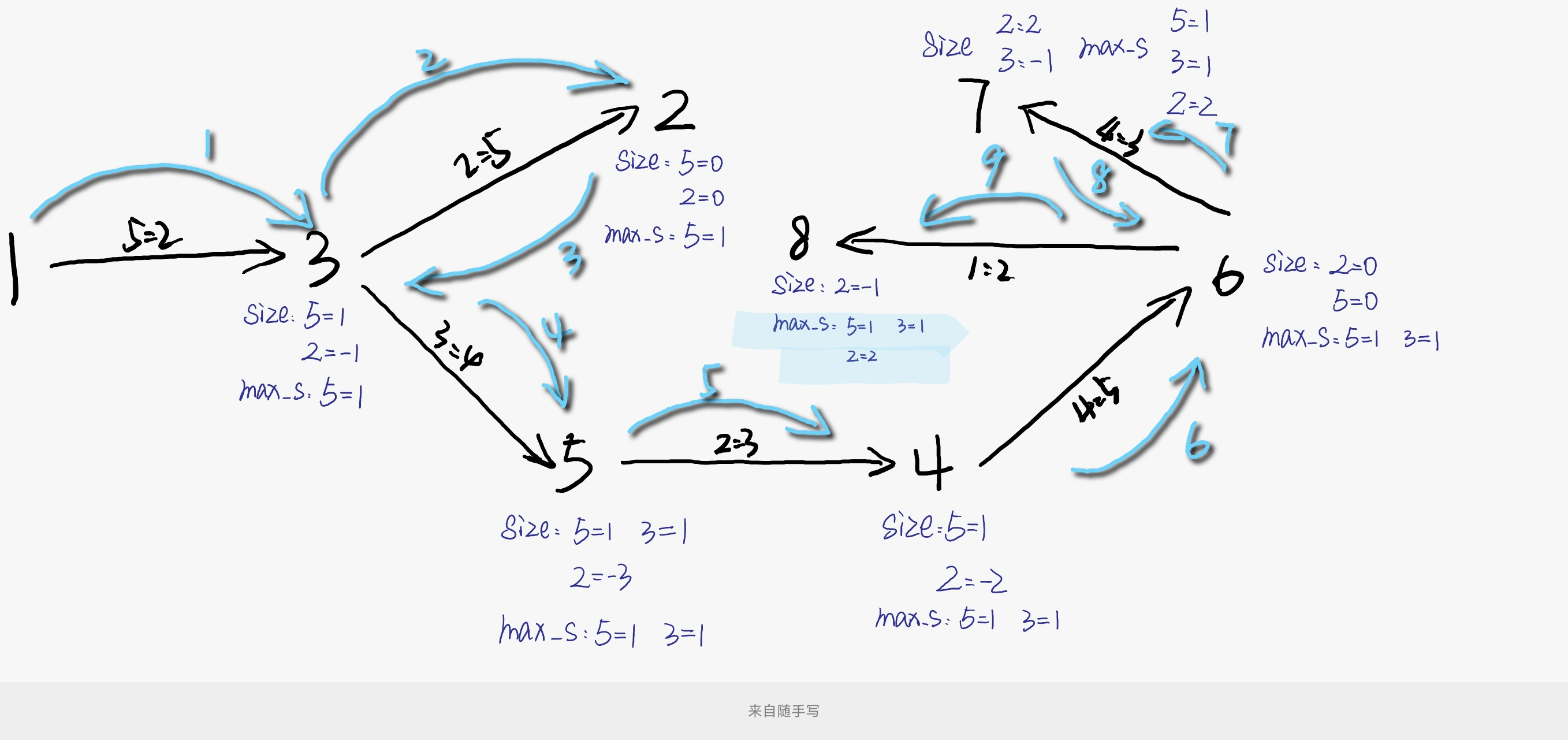
- 使用试除法对每一个 \(p,q\) 分解质因数: \(\mathcal{O}(N*\sqrt N)\) 。
- 递推+预处理所有数的质因数:\(\mathcal O(N*logN)\) 。
- 在第一轮处理的同时计算结果(压缩掉第二次 \(\tt{}DFS\) ):常数减小。
AC代码
点击查看代码
其中 \(Z\) 代表的是大整数类,此处略。
//====================
const int N = 2e5 + 7;
map<int, int> mp, max_size;
vector<PIII> ver[N];
int vis[N];
Z ans, w[N];
//====================
void add(int x, int type) {
for (int i = 2; i <= x / i; ++ i) {
while (x % i == 0) {
max_size[i] = max(max_size[i], mp[i] += type);
x /= i;
}
}
if (x > 1) max_size[x] = max(max_size[x], mp[x] += type);
}
void dfs(int x) {
vis[x] = 1;
for (auto [y, fz, fm] : ver[x]) {
if (vis[y]) continue;
add(fm, -1), add(fz, 1);
dfs(y);
add(fz, -1), add(fm, 1);
}
}
void dfs_w(int x) {
vis[x] = 1;
ans += w[x];
for (auto [y, fz, fm] : ver[x]) {
if (vis[y]) continue;
w[y] = w[x] / fz * fm;
dfs_w(y);
}
}
void Solve() {
int n; cin >> n;
//Clear
for (int i = 1; i <= n; ++ i) vis[i] = 0, ver[i].clear();
mp.clear(), max_size.clear();
for (int i = 1; i < n; ++ i) {
int x, y, fz, fm; cin >> x >> y >> fz >> fm;
ver[x].pb({y, fz, fm}), ver[y].pb({x, fm, fz});
}
dfs(1);
//Clear
for (int i = 1; i <= n; ++ i) vis[i] = 0, w[i] = 0;
ans = 0, w[1] = 1;
for (auto [i, j] : max_size) w[1] *= mypow((Z)i, j); //在这里错了七次……
dfs_w(1);
cout << ans.val() << endl;
}
错误次数
(补题 2 次)预处理时直接套用数组大小,导致 RE 。
(补题 2 次)未对 \(p,q\) 预先做 \(\tt{}gcd\) 处理(后续才发现,此处的 \(\tt{}gcd\) 可以不做,但是相应的, \(\tt{}add\) 函数的顺序需要唯一(例如比例为 \(4:2\) 时,若 \(\tt{}add\) 函数先处理了 \(4\) ,那么 \(\tt{}max\_size[2]\) 会多出 \(1\) 来;而先处理 \(2\) 则不会发生这种情况)。
(补题 7 次)大整数类与 \(\tt{}int\) 型共存的转化出现问题(使用的快速幂是针对大整数类的,没有取模操作,而我直接将 \(\tt{}int\) 型传入,导致整型溢出,但是没有报错,找了好久好久……)错误代码展示
参考借鉴
难题学习不易,在此附上参考借鉴的所有内容。
B站 - 电音抖腿不能改 ,B站 - gzchenben ,知乎 - pzr (大佬的图解让我明白了思路的核心原理),Codeforces - platelet(大佬的代码风格非常清晰明了,借鉴许多)。
文 / WIDA
2022.03.34 成文
首发于WIDA个人博客,仅供学习讨论



 浙公网安备 33010602011771号
浙公网安备 33010602011771号