BLOG-1
题目集二:7-2 串口字符解析
1. 前言:本题主要涉及知识点为运用正则表达式来判断是否有0
2. 设计与分析:
(1)判断是否是长度大于最小结构:
1个起始位‘0’+八个有效数据+一个奇校验位+一个结束位 = 11位;
(2)判断是否有0:
通过正则表达式来判断;
(正则表达式相关语法:正则表达式 – 语法 | 菜鸟教程 (runoob.com))
(3)开始找0:
找到0后开始对他后面10位做处理;
(4)先判断最后一位是不是结束1;
(5)再判断是否奇校验正确;
(6)通过两次判断结果来输出。
源码:
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); String ch; boolean validate=false,parity=false; int start=0,j=0,num=1,sum=0; ch=input.next(); if(ch.length()<11) { System.out.println("null data"); return; } if(ch.matches("^[1]*$")) { System.out.print("null data"); return; } for(start=0;start<ch.length()-10;start++) { if(ch.charAt(start)=='0') { System.out.print(num+":"); num++; if(ch.charAt(start+10)=='0') { validate=false; System.out.println("validate error"); return; } else { validate=true; sum=0; for(j=start+1;j<start+9;j++) { if(ch.charAt(j)=='1') sum++; } if(sum%2==0) { if(ch.charAt(start+9)=='1') parity=true; else { parity=false; System.out.println("parity check error"); return; } } else { if(ch.charAt(start+9)=='0') parity=true; else { parity=false; System.out.println("parity check error"); return; } } } if(validate=true) { if(parity=true) { for(j=start+1;j<start+9;j++) System.out.print(ch.charAt(j)); System.out.print("\n"); } } start=start+10; } } } }
3. 采坑心得:运用正则表达式进行判断时发生错误
4. 改进建议:此代码对于两组异常值同时出现的情况输出错误——只能输出一行(1:validate error),正常情况应为(1:validate error \n 2:validate error)
题目集三:
1. 前言:题目集三涉及知识点:
(1)以空格、逗号以及冒号分隔的输入格式(基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y);
String a=input.nextLine(); String point[]=a.split(" "); String num[]=null; num=point[0].split(","); double x1=Double.valueOf(num[0]); double y1=Double.valueOf(num[1]);
String a=input.nextLine(); String[] b=a.split(":"); String[] d1=c[0].split(","); String[] d2=c[1].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]);
(2)点,线,三角形之间的关系及性质。
7-1 点线形系列1-计算两点之间的距离
1. 设计与分析:
源码:
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); String a=input.nextLine(); String point[]=a.split(" "); String num[]=null; for(String i:point) { num = i.split(","); for(String j:num) { //正则表达式 if(!j.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")) { System.out.print("Wrong Format"); System.exit(0); } } } if(point.length!=2) { System.out.print("wrong number of points"); System.exit(0); } num=point[0].split(","); double x1=Double.valueOf(num[0]); double y1=Double.valueOf(num[1]); num=point[1].split(","); double x2=Double.valueOf(num[0]); double y2=Double.valueOf(num[1]); if(x1==x2&&y1==y2) { System.out.println("Wrong Format"); return; } System.out.print(Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))); } }
7-2 点线形系列2-线的计算
1. 设计与分析:
源码:
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); String a=input.nextLine(); String[] b=a.split(":"); switch(b[0]) { case "1": String[] c=b[1].split(" "); if(c.length!=2) { System.out.print("wrong number of points"); } else { String[] d1=c[0].split(","); String[] d2=c[1].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double k=(y2-y1)/(x2-x1); if(x1==x2&&y1==y2) { System.out.print("points coincide"); } else if(x1==x2) { System.out.print("Slope does not exist"); } else { System.out.print(k); } } break; case "2": String[] d=b[1].split(" "); if(d.length!=3) { System.out.print("wrong number of points"); } else { String[] d1=d[0].split(","); String[] d2=d[1].split(","); String[] d3=d[2].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); if(x2==x3&&y2==y3) { System.out.print("points coincide"); } double k1=(y3-y2)/(x3-x2); double m=y2-k1*x2; double s=(Math.abs((y3 - y2) * x1 + (x2 - x3) * y1 + ((x3 * y2) - (x2 * y3)))) / (Math.sqrt(Math.pow(y3 - y2, 2) + Math.pow(x2 - x3, 2))); System.out.print(s); } break; case "3": String[] e=b[1].split(" "); if(e.length!=3) { System.out.print("wrong number of points"); } else { String[] d1=e[0].split(","); String[] d2=e[1].split(","); String[] d3=e[2].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); double k2=(y2-y1)/(x2-x1); double k3=(y3-y1)/(x3-x1); if(x2==x3&&y2==y3) { System.out.print("points coincide"); } else if(k2==k3) { System.out.print("true"); } else { System.out.print("false"); } } break; case "4": String[] f=b[1].split(" "); if(f.length!=4) { System.out.print("wrong number of points"); } else { String[] d1=f[0].split(","); String[] d2=f[1].split(","); String[] d3=f[2].split(","); String[] d4=f[3].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); double x4=Double.parseDouble(d4[0]); double y4=Double.parseDouble(d4[1]); double k4=(y2-y1)/(x2-x1); double k5=(y4-y3)/(x4-x3); if((x1==x2&&y1==y2)||(x3==x4&&y3==y4)) { System.out.print("points coincide"); } else if(x2==x1&&x4==x3) { System.out.print("true"); } else if(k4==k5) { System.out.print("true"); } else { System.out.print("false"); } } break; case "5": String[] g=b[1].split(" "); if(g.length!=4) { System.out.print("wrong number of points"); } else { String[] d1=g[0].split(","); String[] d2=g[1].split(","); String[] d3=g[2].split(","); String[] d4=g[3].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); double x4=Double.parseDouble(d4[0]); double y4=Double.parseDouble(d4[1]); if((x1==x2&&y1==y2)||(x3==x4&&y3==y4)) { System.out.print("points coincide"); } double k4=(y2-y1)/(x2-x1); double k5=(y4-y3)/(x4-x3); if(k4==k5) { System.out.print("is parallel lines,have no intersection point"); } else { double A1,B1,C1; A1 = y2 - y1; B1 = x1 - x2; C1 = x2*y1-x1*y2; double A2,B2,C2; A2 = y4 - y3; B2 = x3 - x4; C2 = x4*y3-x3*y4; double x,y; y = (C1 * A2 - C2 * A1) / (A1 * B2 - A2 * B1); x = (C2 * B1 - C1 * B2) / (A1 * B2 - A2 * B1); double dax,xiaox,day,xiaoy; if(x1>x2) { dax = x1; xiaox = x2; } else { dax = x2; xiaox = x1; } if(y1>y2) { day = y1; xiaoy = y2; } else { day = y2; xiaoy = y1; } if(xiaox<x&&x<dax&&xiaoy<y&&y<day) { System.out.println(x+","+y+" "+"true"); } if(x3>x4) { dax = x3; xiaox = x4; } else { dax = x4; xiaox = x3; } if(y3>y4) { day = y3; xiaoy = y4; } else { day = y4; xiaoy = y3; } if(xiaox<x&&x<dax&&xiaoy<y&&y<day) { System.out.println(x+","+y+" "+"true"); } else System.out.println(x+","+y+" "+"false"); } break; } default: System.out.print("Wrong Format"); } } }
2. 采坑心得:未使用正则表达式导致输出格式的错误
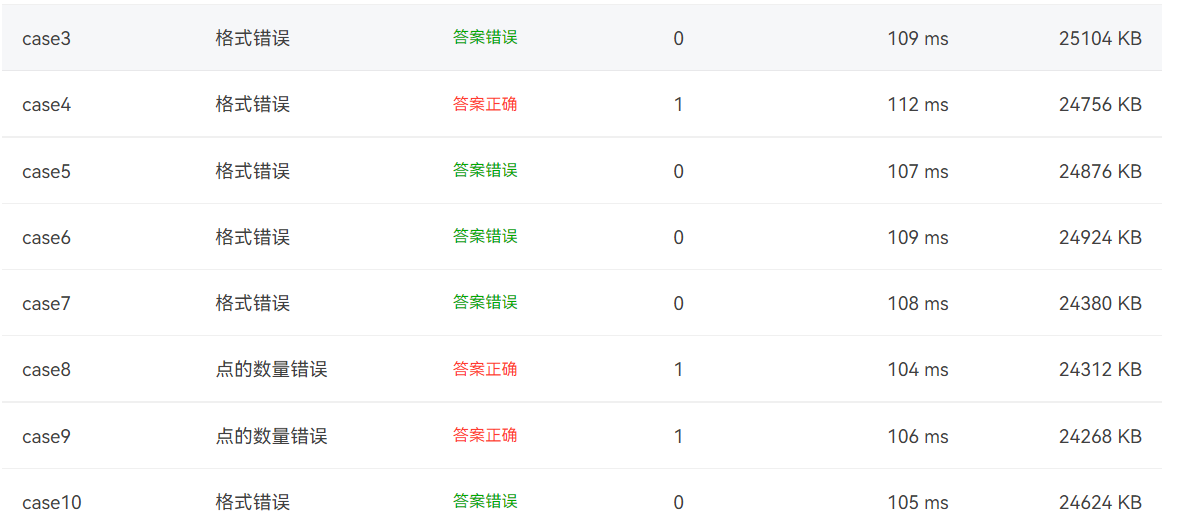
3. 改进建议:
7-3 点线形系列3-三角形的计算
1. 设计与分析:
源码:
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner input=new Scanner(System.in); String a=input.nextLine(); String[] b=a.split(":"); switch(b[0]) { case "1": String[] c=b[1].split(" "); if(c.length!=3) { System.out.print("wrong number of points"); } else { String[] d1=c[0].split(","); String[] d2=c[1].split(","); String[] d3=c[2].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); double A=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); double B=Math.sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2)); double C=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); if(A+B<=C||A+C<=B||B+C<=A) { System.out.print("data error"); return ; } else { if(A==B||A==C||B==C) { System.out.print("true"+" "); if(A==B&&A==C) System.out.print("true"); else System.out.print("false"); } } } break; case "2": String[] d=b[1].split(" "); if(d.length!=3) { System.out.print("wrong number of points"); } else { String[] d1=d[0].split(","); String[] d2=d[1].split(","); String[] d3=d[2].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); double A=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); double B=Math.sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2)); double C=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); if(A+B<=C||A+C<=B||B+C<=A) { System.out.print("data error"); return ; } else { double L=A+B+C; if((L*1000000)%10!=0) { System.out.printf("%.6f ",L); } else { System.out.printf("%f",L); }//周长 double p=(A+B+C)/2; double S=Math.sqrt(p*(p-A)*(p-B)*(p-C)); if((S*1000000)%10!=0) { System.out.printf("%.1f ",S); } else { System.out.printf(S+" "); }//面积 double X=(x1+x2+x3)/3; double Y=(y1+y2+y3)/3; if((X*1000000)%10!=0) { System.out.printf("%.6f",X); System.out.print(","); } else { System.out.print(X+","); } if((Y*1000000)%10!=0) { System.out.printf("%.6f",Y); } else { System.out.print(Y); } } } break; case "3": String[] e=b[1].split(" "); if(e.length!=3) { System.out.print("wrong number of points"); } else { String[] d1=e[0].split(","); String[] d2=e[1].split(","); String[] d3=e[2].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); double A=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); double B=Math.sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2)); double C=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); if(A+B<=C||A+C<=B||B+C<=A) { System.out.print("data error"); return ; } else { if(A*A+B*B<C*C||A*A+C*C<B*B||B*B+C*C<A*A) System.out.print("true false false"); else if(A*A+B*B>C*C||A*A+C*C>B*B||B*B+C*C>A*A) System.out.print("false false true"); else if(A*A+B*B==C*C||A*A+C*C==B*B||B*B+C*C==A*A) System.out.print("false true false"); } } break; case "4": String[] f=b[1].split(" "); if(f.length!=5) { System.out.print("wrong number of points"); } else { String[] d1=f[0].split(","); String[] d2=f[1].split(","); String[] d3=f[2].split(","); String[] d4=f[3].split(","); String[] d5=f[4].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); double x4=Double.parseDouble(d4[0]); double y4=Double.parseDouble(d4[1]); double x5=Double.parseDouble(d5[0]); double y5=Double.parseDouble(d5[1]); double A=Math.sqrt((x4-x3)*(x4-x3)+(y4-y3)*(y4-y3)); double B=Math.sqrt((x4-x5)*(x4-x5)+(y4-y5)*(y4-y5)); double C=Math.sqrt((x5-x3)*(x5-x3)+(y5-y3)*(y5-y3)); if(A+B<=C||A+C<=B||B+C<=A) { System.out.print("data error"); return ; } else if(x1==x2&&y1==y2) { System.out.print("points coincide"); } else { } } break; case "5": String[] g=b[1].split(" "); if(g.length!=4) { System.out.print("wrong number of points"); } else { String[] d1=g[0].split(","); String[] d2=g[1].split(","); String[] d3=g[2].split(","); String[] d4=g[3].split(","); double x1=Double.parseDouble(d1[0]); double y1=Double.parseDouble(d1[1]); double x2=Double.parseDouble(d2[0]); double y2=Double.parseDouble(d2[1]); double x3=Double.parseDouble(d3[0]); double y3=Double.parseDouble(d3[1]); double x4=Double.parseDouble(d4[0]); double y4=Double.parseDouble(d4[1]); double A=Math.sqrt((x4-x3)*(x4-x3)+(y4-y3)*(y4-y3)); double B=Math.sqrt((x4-x2)*(x4-x2)+(y4-y2)*(y4-y2)); double C=Math.sqrt((x2-x3)*(x2-x3)+(y2-y3)*(y2-y3)); if(A+B<=C||A+C<=B||B+C<=A) { System.out.print("data error"); return ; } System.out.print("in the triangle"); /*else { double ab,ac,ad; double p=(A+B+C)/2; double S=Math.sqrt(p*(p-A)*(p-B)*(p-C)); ab=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); ac=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); ad=Math.sqrt((x1-x4)*(x1-x4)+(y1-y4)*(y1-y4)); double p1=(ab+ac+C)/2; double p2=(ab+ad+B)/2; double p3=(ac+ad+A)/2; double S1=Math.sqrt(p1*(p1-ab)*(p1-ac)*(p1-C))+Math.sqrt(p2*(p2-ab)*(p2-B)*(p2-ad))+Math.sqrt(p3*(p3-A)*(p3-ac)*(p3-ad)); if(ab+ac==C||ab+ad==B||ac+ad==A) System.out.print("on the triangle"); else if(S==S1) System.out.print("in the triangle"); else System.out.print("outof triangle"); }*/ } break; default: System.out.print("Wrong Format"); } } }
2. 采坑心得:第四小问和第五小问(4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle")设计不足,此代码不能实现4、5小问的一部分功能。
总结:
对本阶段三次题目集的综合性总结,学到了Java语言的基本结构,基本掌握Java语言的输入输出格式,但在正则表达式这个知识点上还有很大不足,应持续学习正则表达式的应用,同时对于每道题目应使用多个类的应用,使用面向对象的思想来进行解题。
附录:
正则表达式-语法:正则表达式 – 语法 | 菜鸟教程 (runoob.com)
正则表达式-示例:正则表达式 – 示例 | 菜鸟教程 (runoob.com)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号