二、数字信号处理——DFT及其快速算法(二)
离散傅里叶变换的性质
- 线性
- 循环移位性质
- 循环卷积定理
- 复共轭的DFT
- DFT的共轭对称性
1.线性

例题
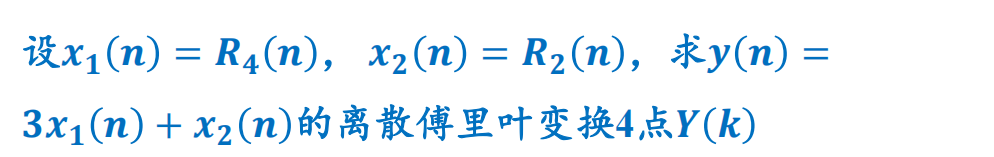
2.循环移位

例题


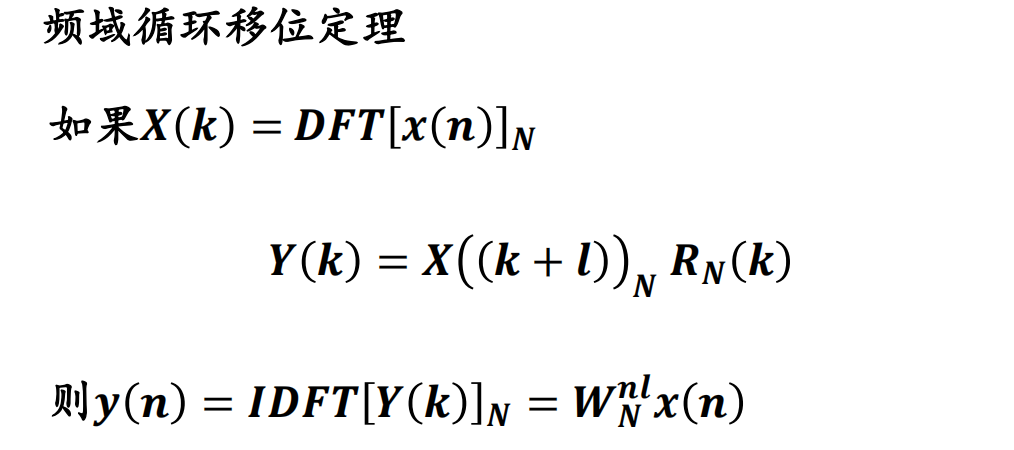
3.循环卷积定理




例题
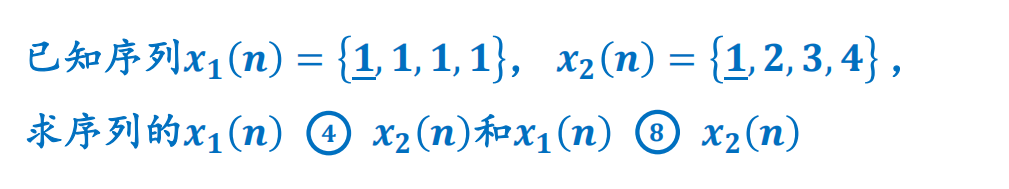
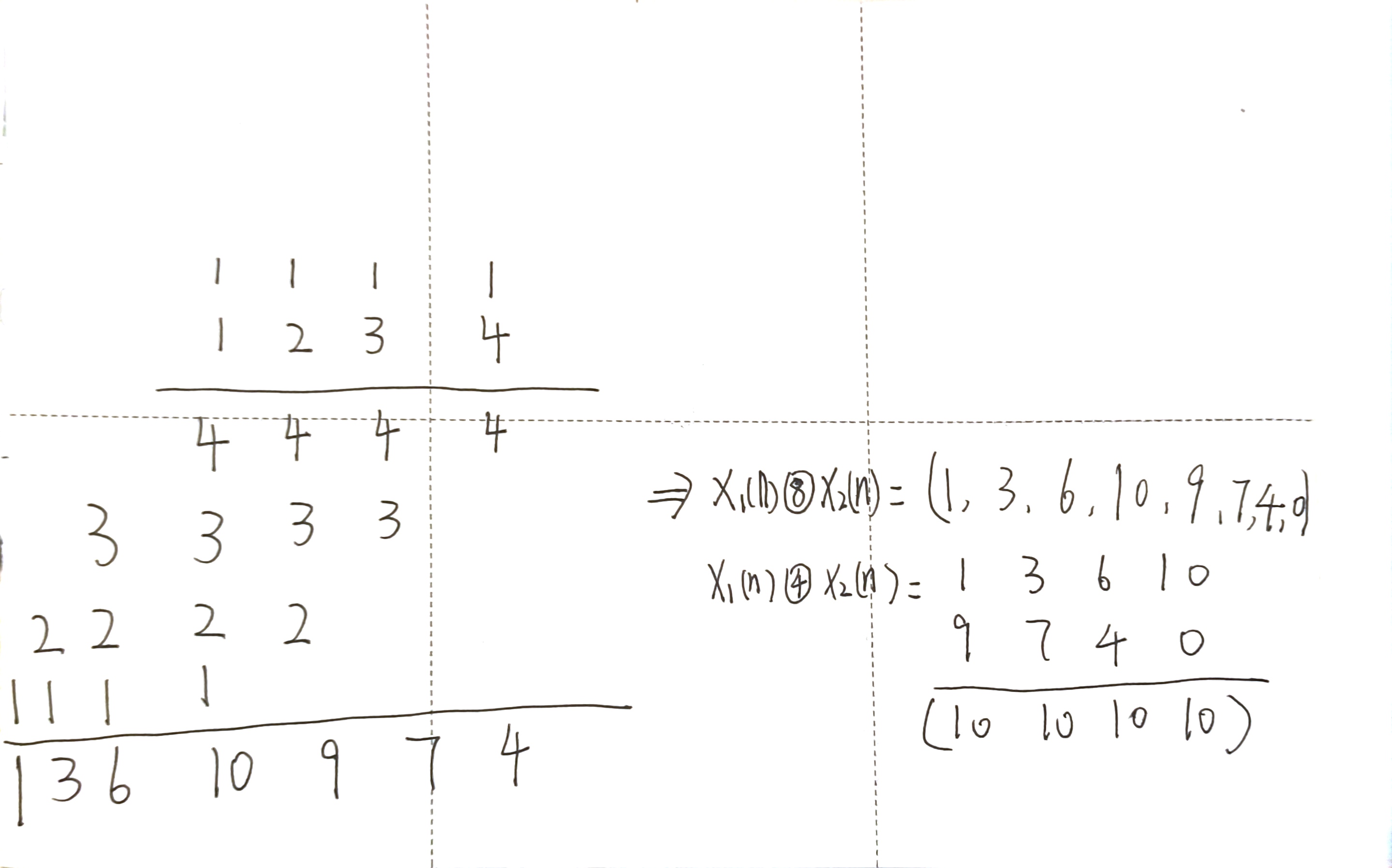
4.复共轭的DFT

例题
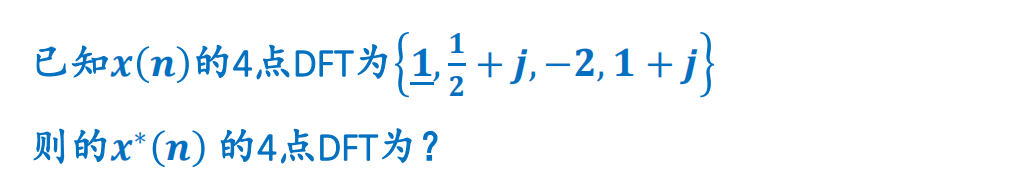
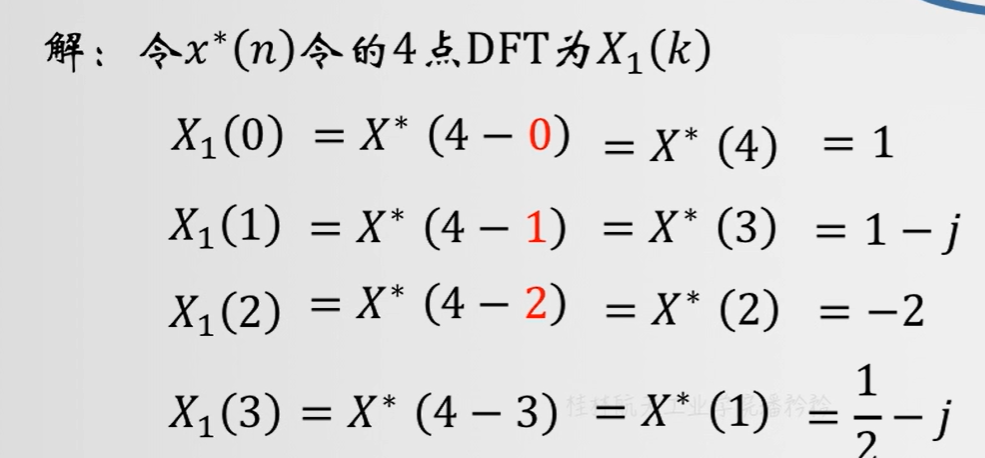
5.DFT的共轭对称性

例题

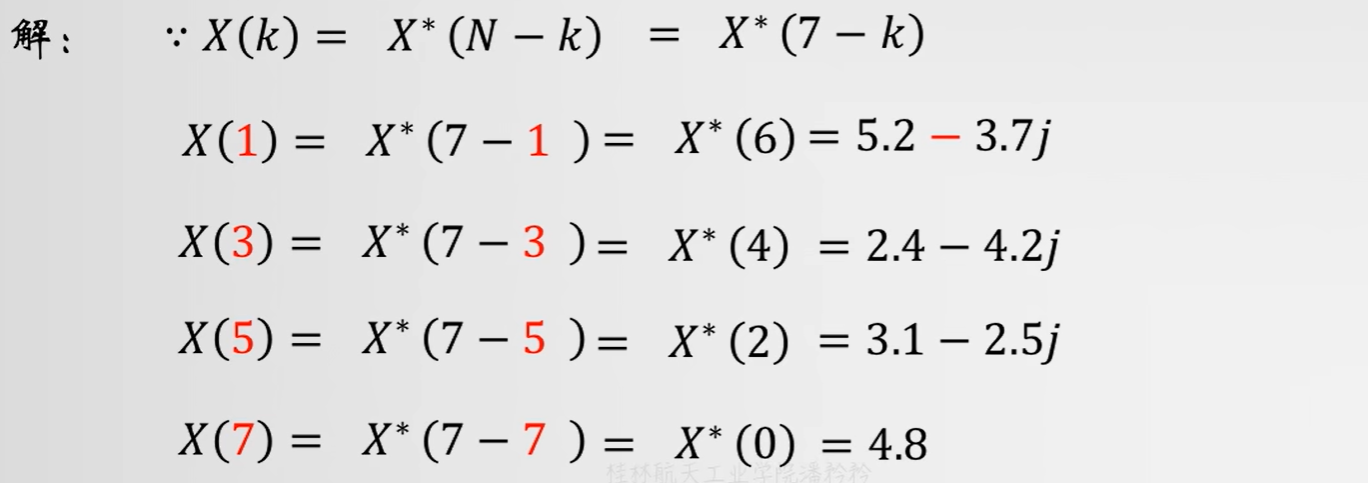
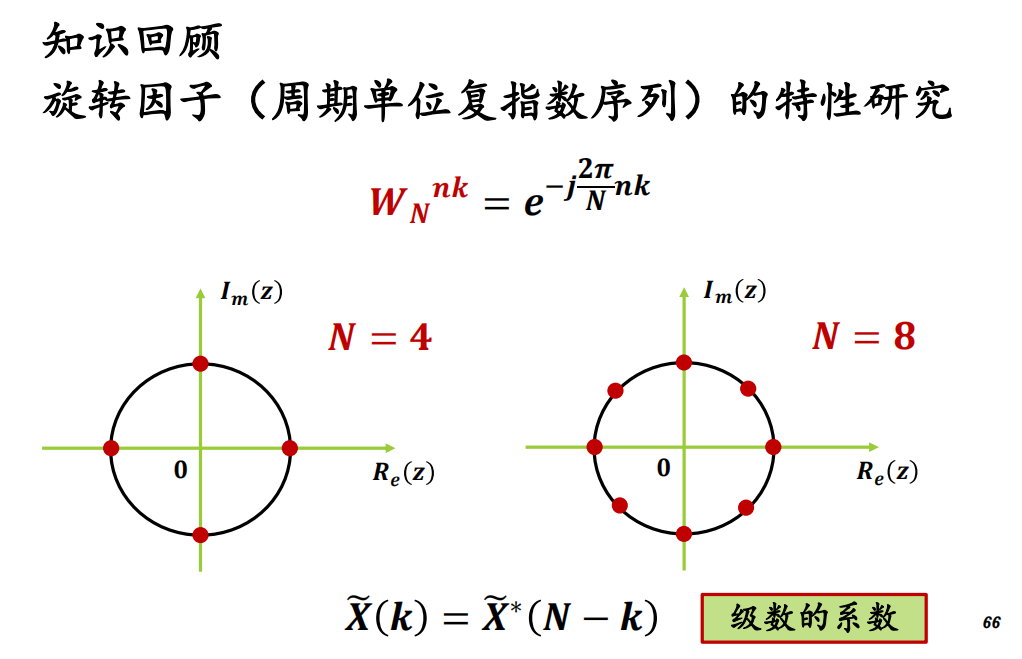
周期序列的傅里叶级数
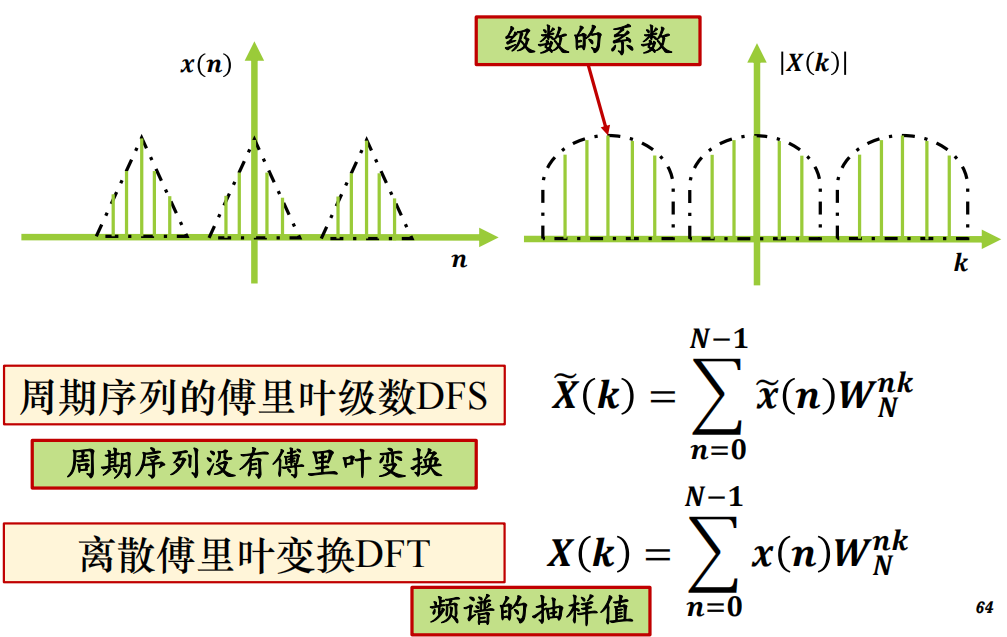
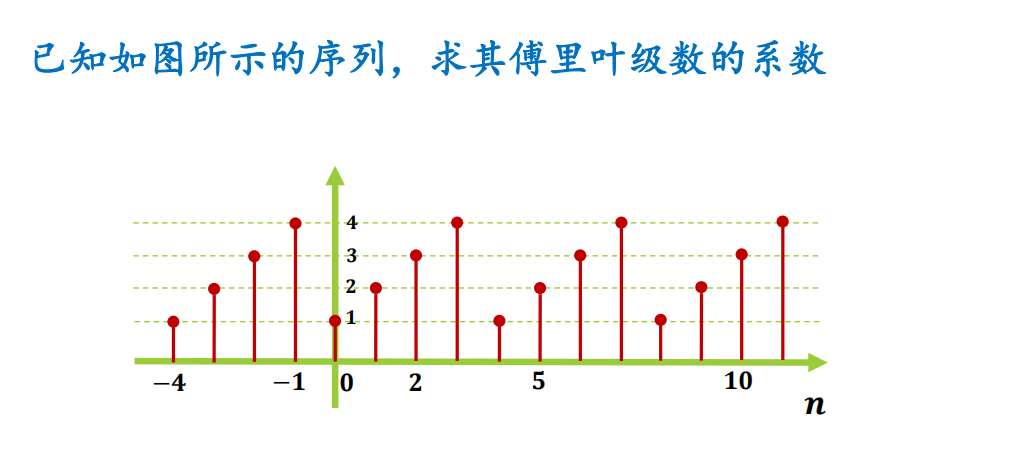

频率域采样
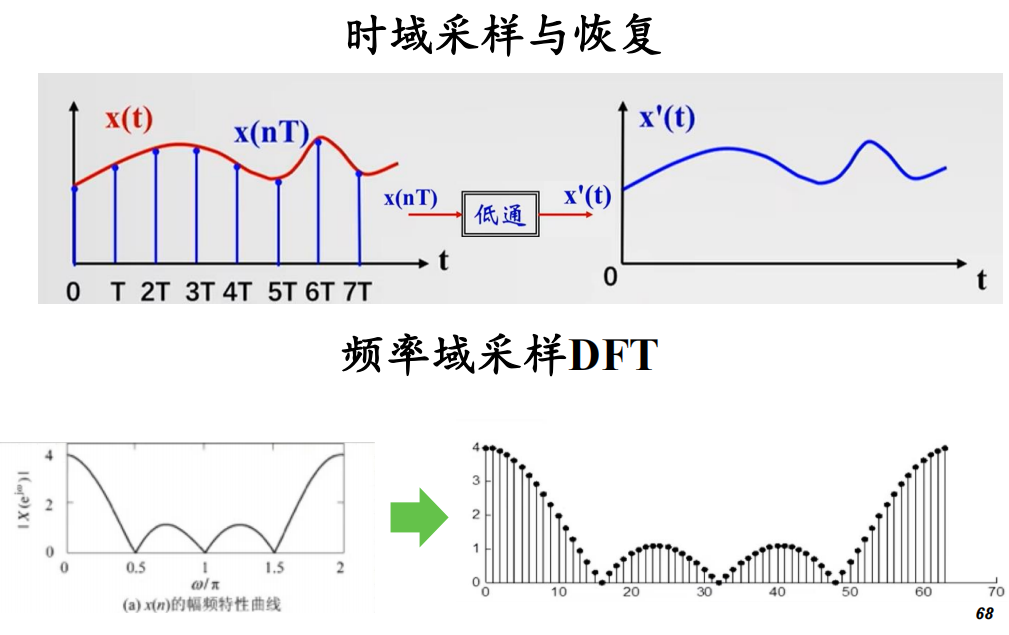

例题



快速傅里叶变换
注:参考B站UP主:讲信号与系统的潘老师
主页:https://space.bilibili.com/400184544


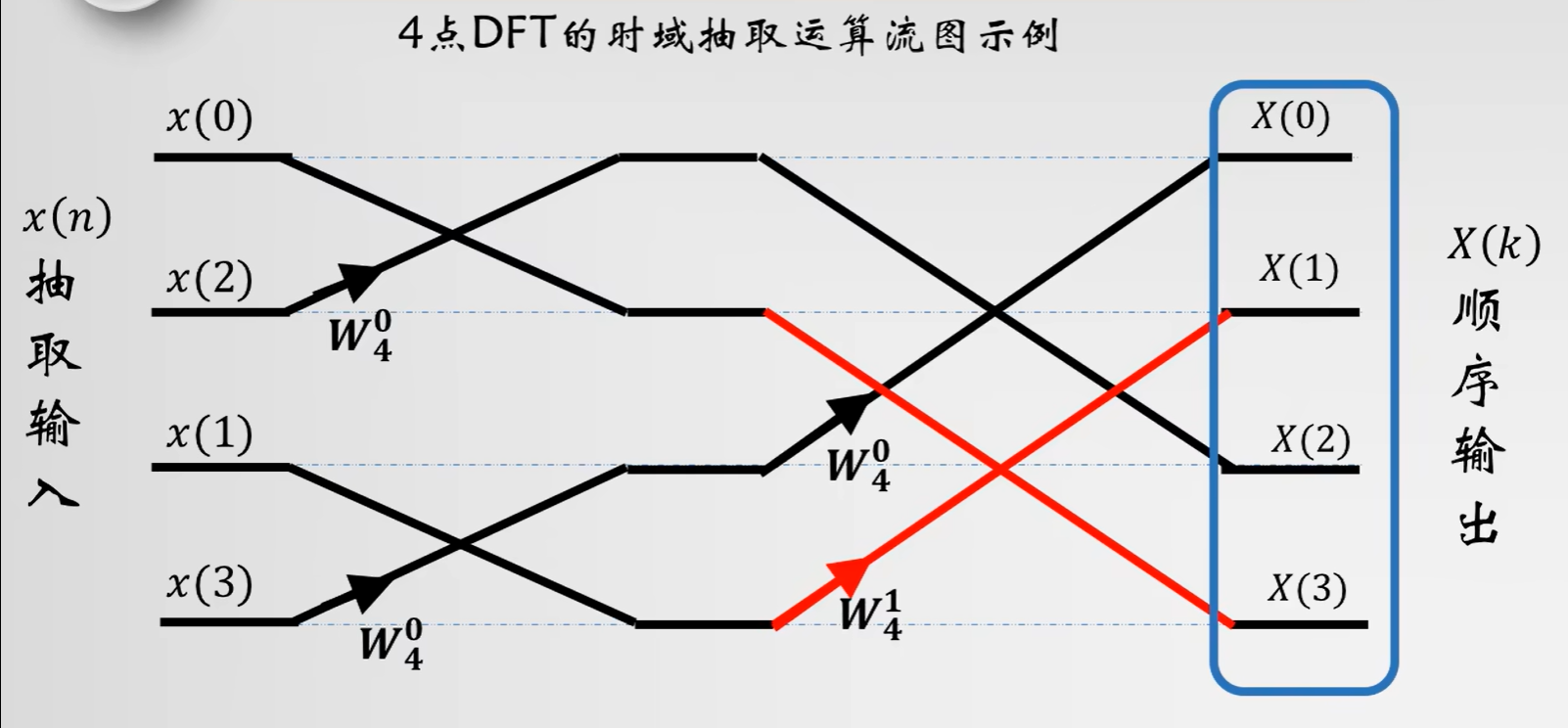
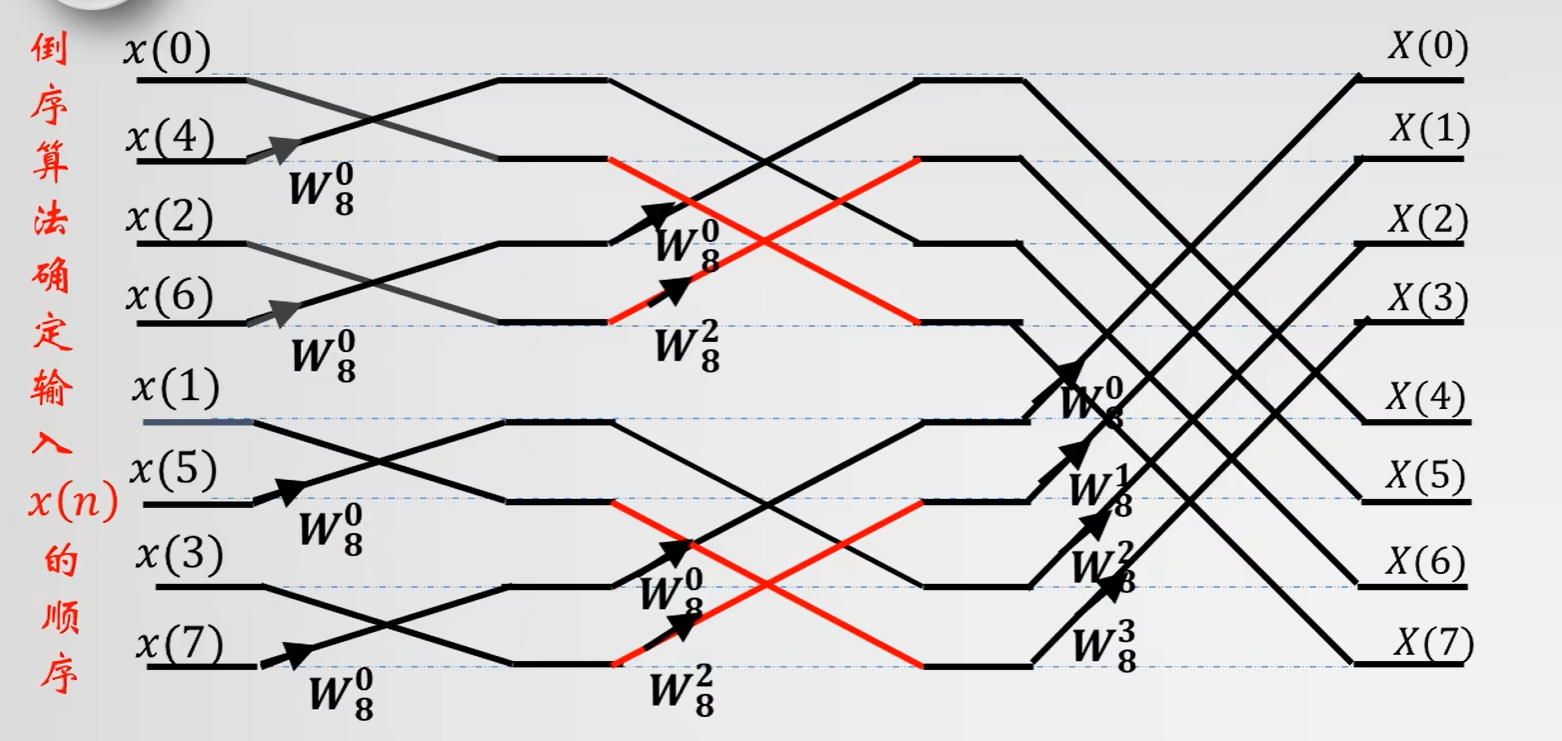
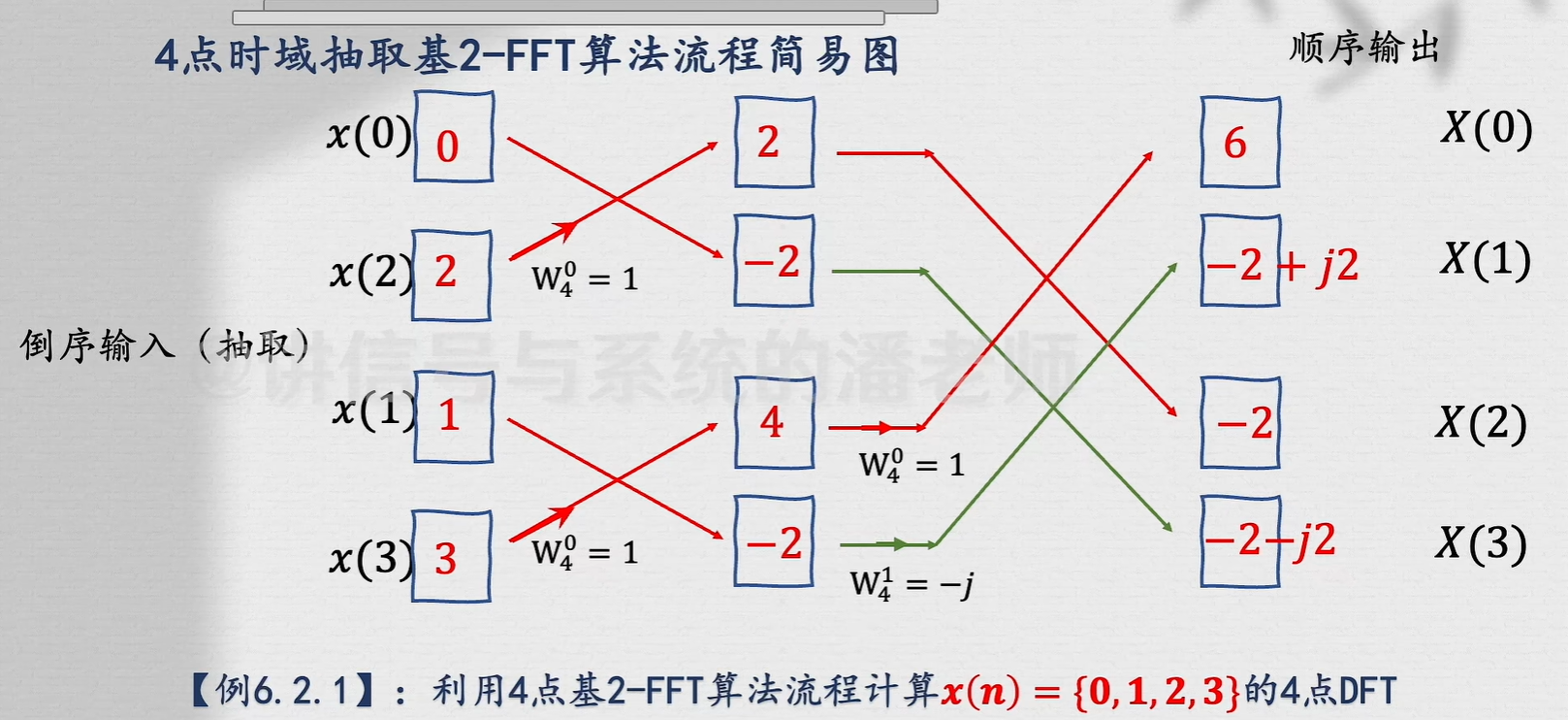
要点:
-
输入的顺序如何排?
- 初始为0,二进制表示为 00 ( 位数是通过点数取2的对数得到,即\(log_2{4}=2\) )
- 第二位为 \(00 + 10 = 10\),也就是十进制的2(在最高位加上1,若有进位,向次高位进位)
- 第三位为 \(10 + 10 = 01\),也就是十进制的1
- 第四位为 \(01 + 10 = 11\),也就是是禁止的3
-
旋转因子放哪里?如何算?
- 旋转因子的位置固定,记下就好
- 第一阶旋转因子有 \(2^0=1\) 个
- 第二阶旋转因子有 \(2^1=2\) 个
- 第三阶旋转因子有 \(2^2=4\) 个
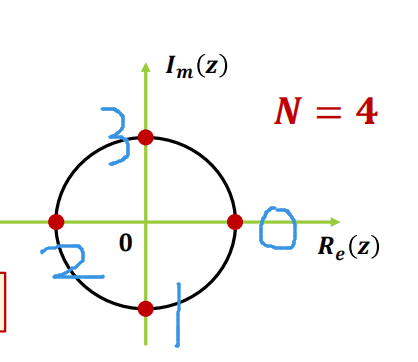
- 如何算的问题,以此题4个点为例
![image]()
![image]()
- 则\(w_4^1\)是旋转因子图中的第一个位置,等于 \(-j\)
- 旋转因子的位置固定,记下就好
-
记住运算规律:箭头向上加,向下减,记得乘上旋转因子再加减
例题




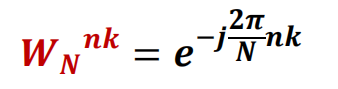

 浙公网安备 33010602011771号
浙公网安备 33010602011771号