第 7 章:常微分方程的数值解法(二)
7.4 龙格-库塔法
龙格-库塔法的基本思想
- 欧拉公式可以写成
![image]()
- 则\(y_{i+1}\)的表达式与\(y(x_{i+1})\)的泰勒展开式的前两项完全相同,即局部截断误差为\(O(h^2)\)
- 改进的欧拉公式又可以写成
![image]()
- 上述两个公式在形式上都有一个共同特点,都是用\(f(x,y)\)在某些点上值的线性组合得出\(y(x_{i+1})\)的近似值\(y_{i+1}\),而且增加计算\(f(x,y)\)的次数,可提高截断误差的阶。
- 于是可考虑用函数\(f(x,y)\)在若干点上的函数值的线性组合来构造近似公式,构造时要求近似公式在(x_i,y_i)处的泰勒展开式与解\(y(x)\)在\(x_i\)处的泰勒展开式的前面几项重合,从而使得近似公式达到需要的阶数。既避免求偏导,又提高了计算方法精度的阶数。
- 或者这样说,在\([x_i,x_{i+1}]\)这一步多预报几个点的斜率值,然后将其加权平均作为平均斜率,则可构造出更高精度的计算格式,这就是龙格-库塔法的基本思想
二阶龙格库塔法
在\([x_i,x_{i+1}]\)上取两点\(x_i\)和\(x_{i+p}=x_i+ph\),以该两点处斜率值\(k_1\)和\(k_2\)的加权平均(或称为线性组合)来求取平均斜率\(k^*\)的近似值\(K\),即
\[K = \lambda_1 k_1 + \lambda_2 k_2
\]
- 式子中,\(k_1\)是\(x_i\)点处的切线的斜率值,\(k_1=f(x_i,y_i)=y'(x_i),k_2\)为\(x_i+ph\)点处的切线斜率值,比照该进的欧拉法,将\(x_{i+p}\)视为\(x_{i+1}\),即可得到
\[k_2 = f(x_i + ph, y_i + phk_1)
\]
- 对常微分方程初值问题的解\(y=y(x)\),根据微分中值定理,存在点\(\xi \in (x_i, x_{i+1})\)使得
\[y(x_{i+1}) - y(x_i) = y'(\xi)(x_{i+1} - x_i)
\]
- 也即
\[y(x_{i+1}) = y(x_i) + hK
\]
- 式中,\(K = y'(\xi) = f(\xi, y(\xi))\)
- \(K\)可以看做是\(y=y(x)\)在区间\([x_i,x_{i+1}]\)上的平均斜率
- 所以可得计算公式为
\[\begin{align*}
y(x_{i+1}) &= y(x_i) + hK \\
&= y(x_i) + h(\lambda_1 k_1 + \lambda_2 k_2)
\end{align*}\]
- 将\(y(x_{i+1})\)在\(x=x_i\)处进行二阶泰勒展开
\[y(x_{i+1}) = y(x_i) + hy'(x_i) + \frac{h^2}{2!}y''(x_i) + O(h^3)
\]
- 将$$在\(x=x_i\)处进行一阶泰勒展开
\[\begin{align*}
k_2 &= f(x_i, y_i) + ph \left[ f_x(x_i, y_i) + f(x_i, y_i) f_y(x_i, y_i) \right] + O(h^2) \\
&= y'(x_i) + ph \cdot y''(x_i) + O(h^2)
\end{align*}\]
- 将以上结果带入\(y(x_{i+1}) = y(x_i) + hK = y(x_i) + h(\lambda_1 k_1 + \lambda_2 k_2)\),得
\[\begin{align*}
y(x_{i+1}) &= y(x_i) + h(\lambda_1 k_1 + \lambda_2 k_2) \\
&= y(x_i) + h\left\{\lambda_1 y'(x_i) + \lambda_2 \left[ y'(x_i) + ph \cdot y''(x_i) + O(h^2) \right] \right\} \\
&= y(x_i) + h(\lambda_1 + \lambda_2) y'(x_i) + \lambda_2 ph^2 y''(x_i) + O(h^3)
\end{align*}\]
- 对\((x_{i+1}) = y(x_i) + hy'(x_i) + \frac{h^2}{2!}y''(x_i) + O(h^3)\) 和 上式进行比较可知,只要
\[\left\{
\begin{array}{l}
\lambda_1 + \lambda_2 = 1 \\
\lambda_2 \cdot p = \frac{1}{2}
\end{array}
\right.\]
- 成立,格式\(y(x_{i+1}) = y(x_i) + hK = y(x_i) + h(\lambda_1 k_1 + \lambda_2 k_2)\)的局部截断误差就等于\(O(h^3)\)
- 上式有三个未知量,但只有两个方程,因而有无穷多个解。可以取\(\lambda_1 = \lambda_2 = \frac{1}{2}\),则\(p=1\),这是无穷多解中的一个解,将以上所解的值代入式子\((x_{i+1}) = y(x_i) + hy'(x_i) + \frac{h^2}{2!}y''(x_i) + O(h^3)\)并改写可得
\[\left\{
\begin{array}{l}
y_{i+1} = y_i + \frac{h}{2}(k_1 + k_2) \\
k_1 = f(x_i, y_i) \\
k_2 = f(x_{i+1}, y_i + hk_1)
\end{array}
\right.\]
- 不难发现,上面的格式就是该进的欧拉格式。凡是满足条件式
\[\left\{
\begin{array}{l}
\lambda_1 + \lambda_2 = 1 \\
\lambda_2 \cdot p = \frac{1}{2}
\end{array}
\right.\]
- 并且有一簇形如上式的计算格式,这些格式统称为二阶龙格-库塔格式。因此改进的欧拉格式是众多龙格-库塔法中的一个特殊格式
- 若取\(\lambda_1=0\),则\(\lambda_2=1,p=1/2\),此时龙格-库塔法的计算公式为
\[\left\{
\begin{array}{l}
y_{i+1} = y_i + h k_2 \\
k_1 = f(x_i, y_i) \\
k_2 = f\left(x_{i+\frac{1}{2}}, y_i + \frac{h}{2} k_1\right)
\end{array}
\right.\]
- 这个计算公式称为变形的二阶龙格-库塔法(也称为中点公式)。式子\(x_{i+1/2}\)为区间\([x_i,x_{i+1}]\)的中点
三阶龙格-库塔法


四阶龙格-库塔法

龙格-库塔方法的推导是基于泰勒展开方法的,因而它所要求的解具有较好的光滑性,如果解的光滑性差,那么使用四阶龙格-库塔方法求得的数值解,其精度可能反而不如改进的欧拉方法。在实际计算时,应当针对具体问题选择合适的算法
7.5 亚当姆斯法
龙格-库塔方法是一类重要的算法,但是这类算法在每一步都需要先预报几个点上的斜率值,计算量比较大。考虑到计算\(y_{i+1}\)之前已经得到一系列节点上\(x_i,x_{i-1},...,x_i\)的斜率值,能否利用这些已知值来减少计算量呢?这就是亚当姆斯法的思想
- 设用\(x_i,x_{i+1}\)两点的斜率值加权平均作为区间\([x_i,x_{i+1}]\)上的平均斜率,有计算格式
![]()
- 选取参数\(\lambda\),使上述格式具有二阶精度
![]()
![]()
![]()
![]()
![]()
![image]()
7.6 算法的稳定性及收敛性
稳定性
稳定性在微分方程数值解法中是一个非常重要的问题。因为微分方程初值问题的数值方法是用差分格式进行计算的,而在差分方程的求解过程中,存在着各种计算误差,这些计算误差如舍入误差等引起的扰动,在传播过程中,可能会大量积累,对计算结果的准确性将产生影响。这就涉及到算法稳定性问题




收敛性




7.7 一阶常微分方程与高阶方程


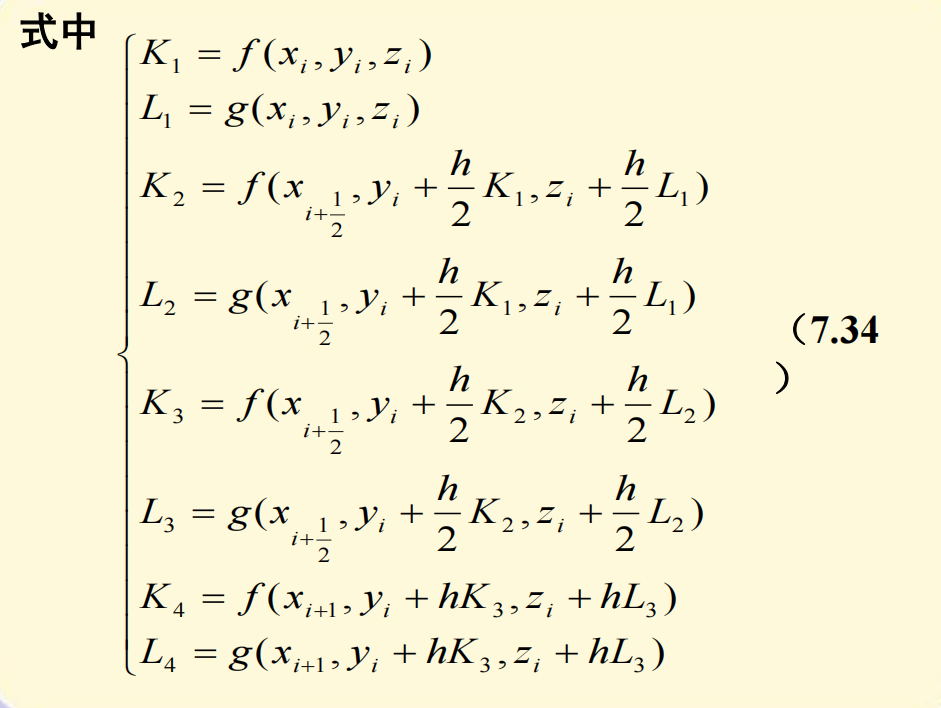



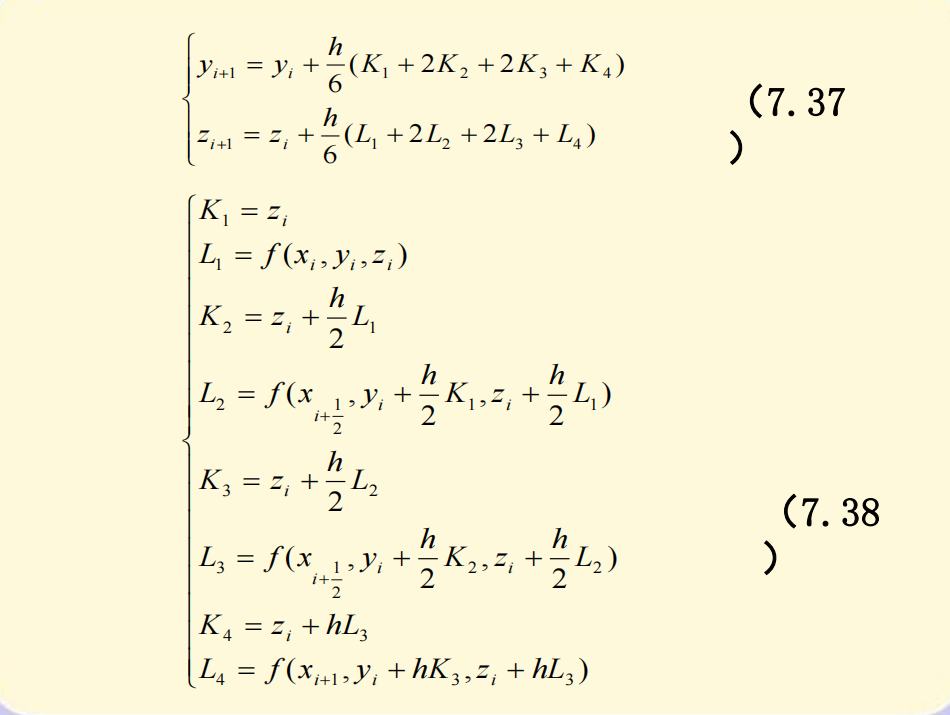


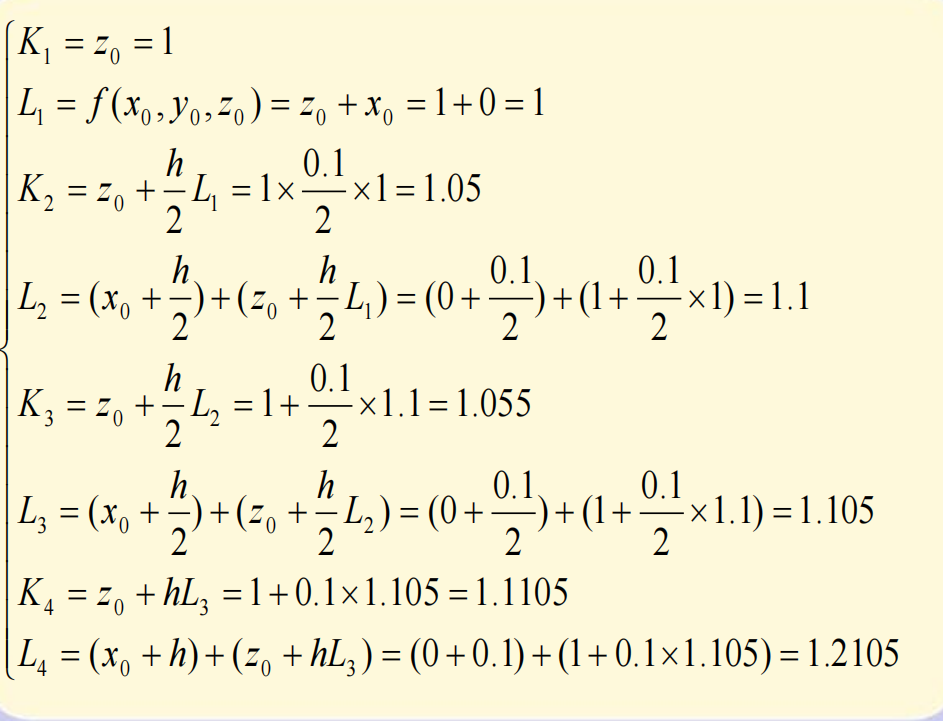

本章介绍了常微分方程初值问题的基本数值解法,包括单步法和多步法。单步法主要有欧拉法、改进欧拉法和龙格-库塔方法。多步法是亚当姆斯法。它们都是基于把一个连续的定解问题离散化为一个差分方程来求解,是一种步进式的方法。用多步法求常微分方程的数值解可获得较高的精度。
实际应用时,选择合适的算法有一定的难度,既要考虑算法的简易性和计算量,又要考虑截断误差和收敛性、稳定性
课后习题




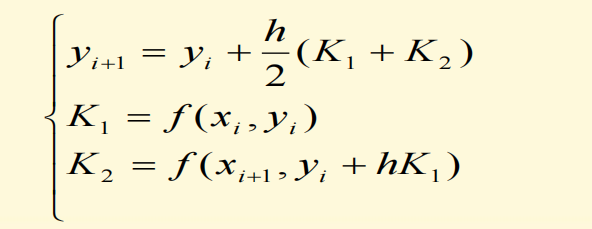








 浙公网安备 33010602011771号
浙公网安备 33010602011771号