第 4 章:解线性方程组的直接法(二)
由前文提到的矩阵的\(LU\)分解派生出解方程组的直接分解法

\(由高斯分解法得到启发,对A的消元过程相当于将A分解为一个上三角阵和一个下三角阵的过程。\)
如果直接分解\(A\)得到\(L\)和\(U\),\(A=LU\),这时候方程组\(AX=b\)化为\(LUX=b\),令\(UX=Y\),由\(LY=b\)解出\(Y\),再由\(UX=Y\)解出\(X\),原方程组的求解问题化为求解两个三角形方程组
- 杜立特尔分解:将方阵\(A\)分解为\(A=LU\),\(L\)是单位下三角阵,\(U\)是上三角阵
- 克劳特分解:将方阵\(A\)分解为\(A=LU\),当\(L\)是下三角阵,\(U\)是单位上三角阵
- 分解的条件:方阵\(A\)的各阶顺序主子式不为零
杜利特尔分解
若\(A\)的各阶顺序主子式不为零,\(A\)可分解为\(A=LU\),其中\(L\)为单位下三角阵,\(U\)为上三角阵,即为
矩阵\(L\)和\(U\)共有\(n^2\)个未知元素,按照一定的顺序,对每个\(a_{ij}\)列出上式对应元素的关系式,一个关系式解出一个\(L\)或\(U\)的元素
按下面的步骤计算\(L\)和\(U\)的元素
- 计算 \(U\) 的第一行元素\(u_{11},u_{12},...,u_{1n}\)
- 要计算\(u_{11}\)则列出上面矩阵中两边的第一行第一列关系式
![image]()
- 故\(u_{11}=a_{11}\)
- 一般地,由\(U\)的第一行元素的关系式
![image]()
- 得到
![image]()
- 计算\(L\)的第一列元素\(l_{21},l_{31},...,l_{n1}\)
- 要计算\(l_{21}\)则列出等号两边第二行第一列的元素
![image]()
- 故有
![image]()
- 一般的,由\(L\)的第一列元素的关系式
![image]()
- 得到
![image]()
- \(计算U的第二行元素\)
- \(计算U的第二列元素\)
若已计算出\(U\)的前\(k-1\)行,\(L\)的\(k-1\)列元素
- 计算\(U\)的第\(k\)行元素\(u_{kk},u_{k,k+1},...,u_{kn}\)
- 由\(U\)的第\(k\)行元素的关系式
![image]()
- 因为\(U\)是上三角阵,所以列标不小于行标,\(j≥k\)
![image]()
- 得到
![image]()
- 计算\(L\)的第\(k\)列元素\(l_{k+1,k},l_{k+2,k},...,l_{nk}\)
- 由\(L\)的第\(k\)列元素的关系式
![image]()
- 因为\(L\)是下三角阵,所以行标不小于列标,\(i≥k\)
![image]()
- 得到
![image]()
- 一直做到\(L\)的第\(n-1\)列,\(U\)的第\(n\)行为止
用LU直接分解方法求解方程组所需要的计算量仍为\(\frac{1}{3}n^3 + O(n^2)\),与用高斯消元法的计算量基本相同
如果需要节省空间,可以将\(U\)以及\(L\)的元素直接放在矩阵\(A\)相应元素的位置上。例如
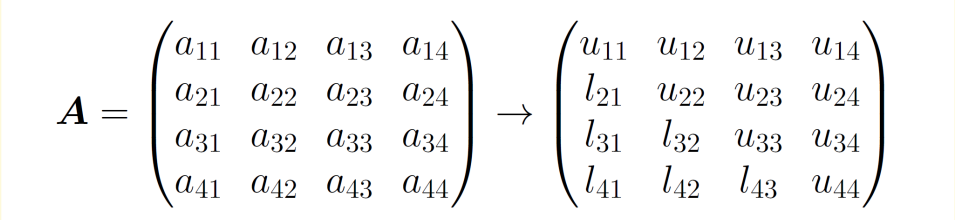
最后在存放\(A\)的数组中得到\(L,U\)的元素
- 用直接分解法解方程\(AX=b\),首先作出分解\(A=LU\),令\(UX=Y\),解方程组\(LY=b\),由于\(L\)是单位下三角阵,容易得到
![image]()
- 再解方程组\(UX=Y\),其中
![image]()
对\(A\)进行LU分解时,并不涉及常数项\(b\),因此,若需要解具有相同系数的一系列线性方程组时。使用直接分解法可以达到事半功倍的效果
例题


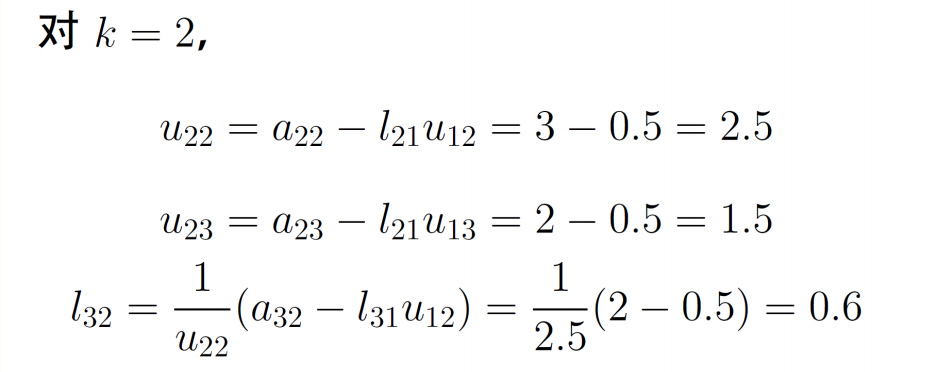
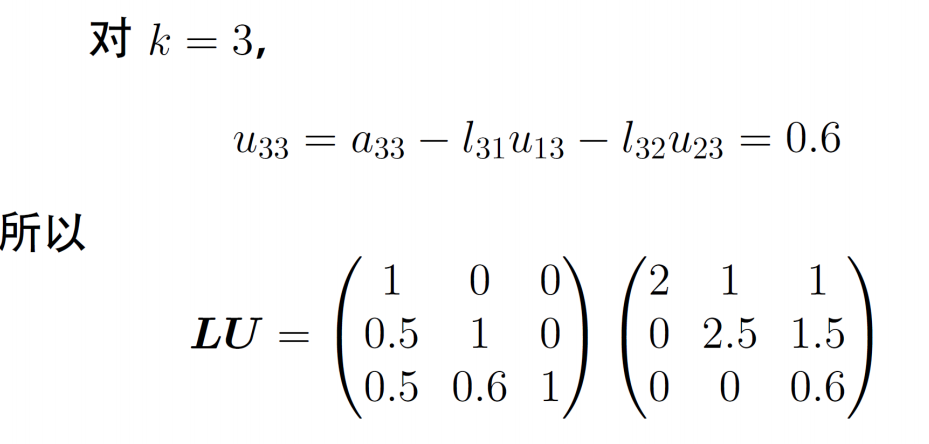
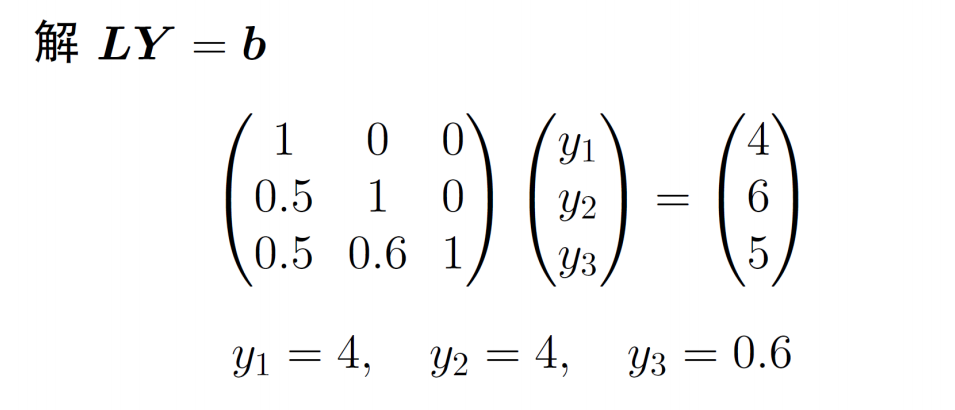
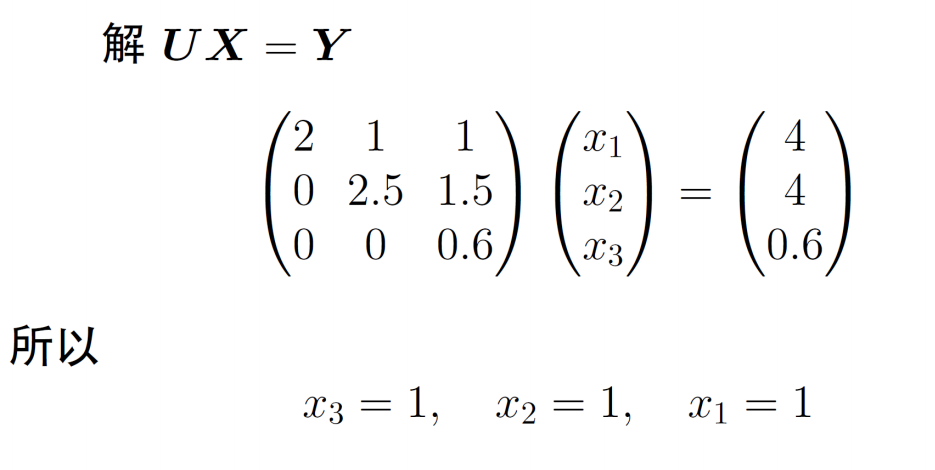
克劳特分解
克劳特分解是在矩阵\(A=LU\)的克劳特分解形式中,\(L\)是下三角矩阵,\(U\)是单位上三角矩阵,记
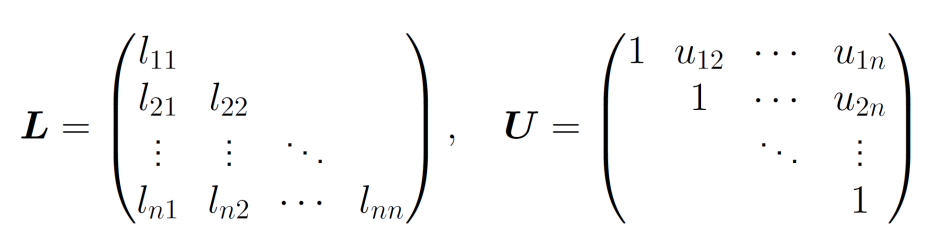
矩阵的克劳特分解与多利特尔分解完全类似,只是次序不同。设\(A\)的各阶顺序主子式不为零,按计算\(L\)的第一列,\(U\)的第一行,...,\(L\)的第\(k\)列,\(U\)的第\(k\)行的顺序进行计算,类似于多利特尔
分解,做\(A=LU\)两边矩阵元素的关系式\(a_{ij} = \sum_{r=1}^{n} l_{ir} u_{rj}\),可导出计算公式,对\(k=1,2,...,n\)
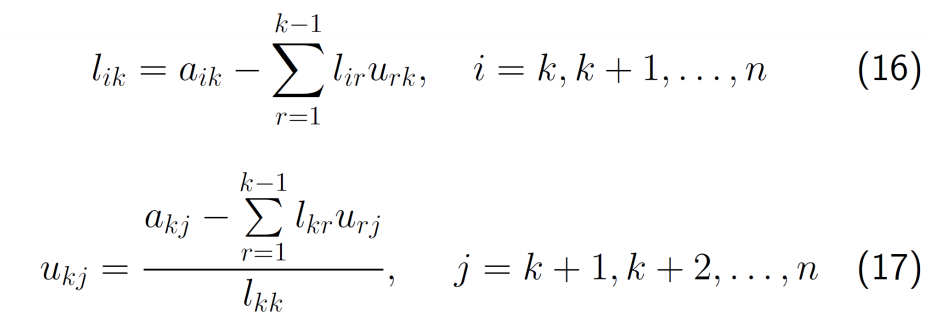

追赶法

- 利用矩阵直接分解法,求解具有三对角系数矩阵的线性方程组十分简单而有效。采用\(Crout\)分解法,分解形如(20)的三对角矩阵\(A=LU\),容易验证,\(L,U\)具有以下形式
- 比较 \(A=LU\) 两边元素,可得到
- 若规定\(c_i = 0\),可得到一般计算公式
- 考虑三对角系数矩阵的线性方程组\(Ax=f\),这里\(x=(x_1,x_2,...,x_n)^T,f=(f_1,f_2,...,f_n)^T\),令\(Ux=y\),则有
- \(Ly=f\)
- 于是有
- 规定\(v_n=0\),由\(Ux=y\)得到
- 事实上,由(21),每计算出一个\(u_i\),就可以按(22)计算出\(y_i\),若规定\(c_1=0\),由(21)和(22)可合并成
- 称上面(23)和(24)的公式为追赶法
- 计算量为\(O(n)\)
对称正定矩阵的\(LDL^T\)分解
正定矩阵:

若\(A\)正定,则存在下三角矩阵\(U\),使得\(A=UU^T\),直接分解\(A=UU^T\)的分解方法,称为平方根分解法。由于在平方根分解法中含有计算平方根的步骤,因此很少采用平方根法的分解形式。对于对称正定矩阵,常用的是\(LDL^T\)分解
对\(A\)做多利特尔分解 \(A=LU\)
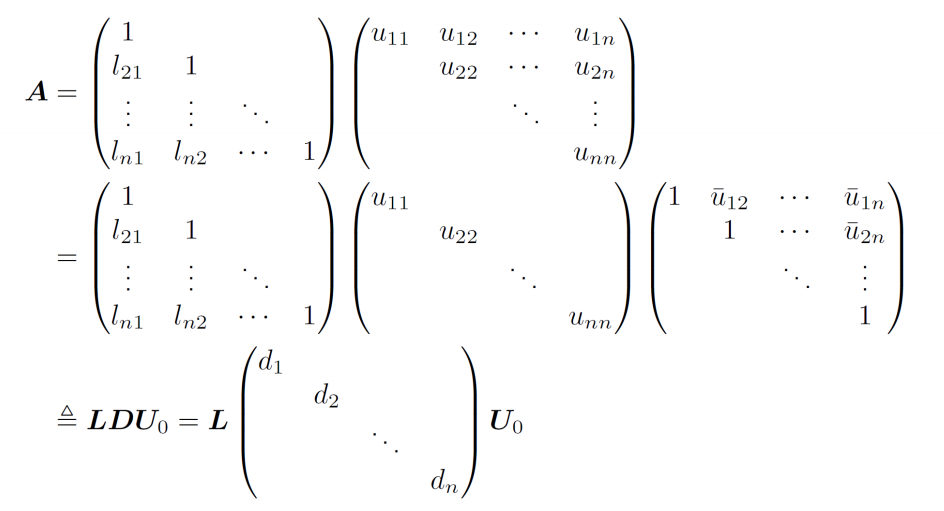
- 又因为\(A=A^T=U_0^TDL^T\),由分解的唯一性即得
- \(T_0^T=L\)
- \(A=LDL^T\)
- \(L\)是对角线元素为1的单位下三角矩阵
对矩阵\(A\)做多利特尔分解或克劳特分解,共需要\(n^2\)个矩阵元素;对称矩阵\(LDL^T\)分解,只需计算\(n(n+1)/2\)个元素,减少了近一半分解元素的工作量
![image]()
![image]()
![image]()
![image]()
- 解三次方程组!
例题



病态方程组
-
定义
![image]()
-
注:非奇异矩阵
![image]()
-
对于线性方程组\(Ax=b\),若系数矩阵有小扰动\(\delta A\),这时方程组的解也有小扰动,于是
- $\delta x $ 受到 \(\delta A\)的影响表示为
- 若常数\(b\)有小扰动,\(\delta b\)的影响表示为
- 因此,称\(Cond(A)\)大的矩阵为“坏矩阵”或者“病态矩阵”,对于条件数大的矩阵,小的误差可能会引起解的失真。
- 一般来说,若\(A\)的按模最大的特征值与按模最小的特征值之比较大时,矩阵就会呈病态
- 特别的,当\(del A\)很小时,\(A\)总是病态的
例子
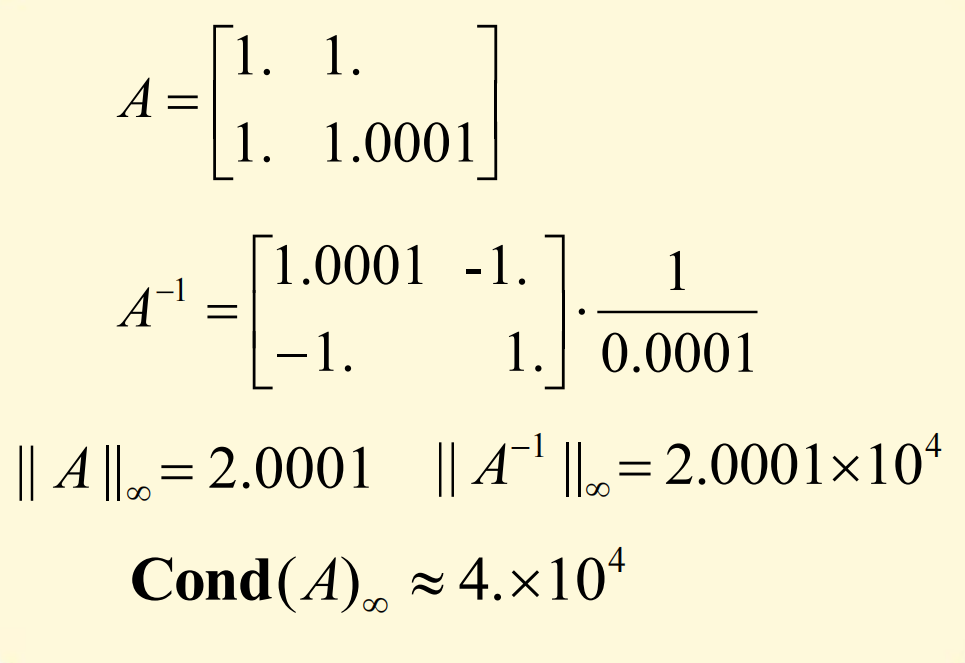
关于病态方程组的解法
- 1.采用高精度的算术运算
- 2.采用预处理方法
- 3.平衡方法
课后习题


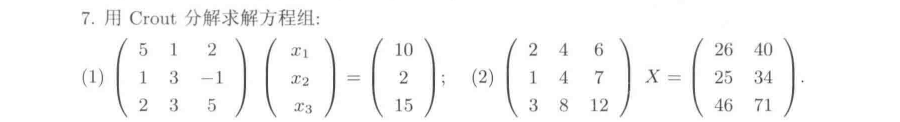


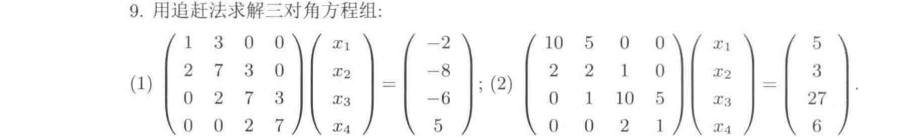


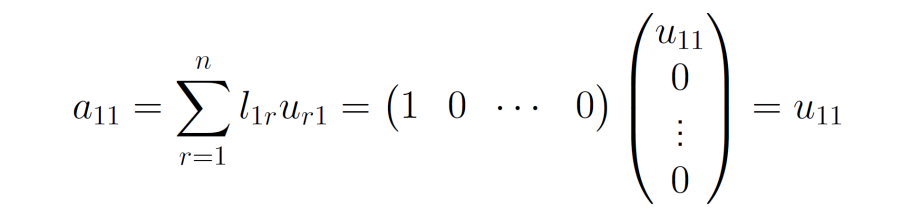
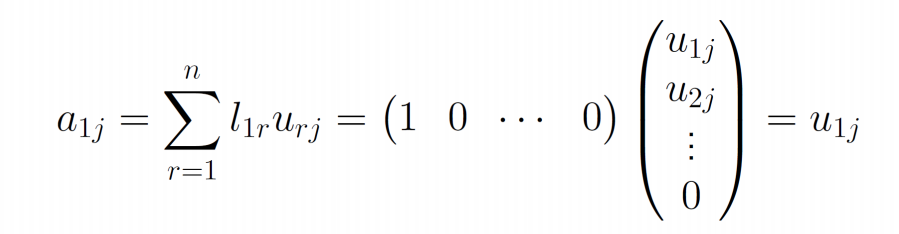
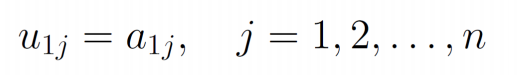
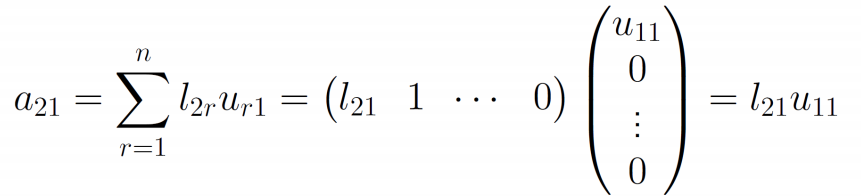
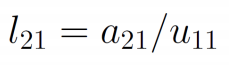
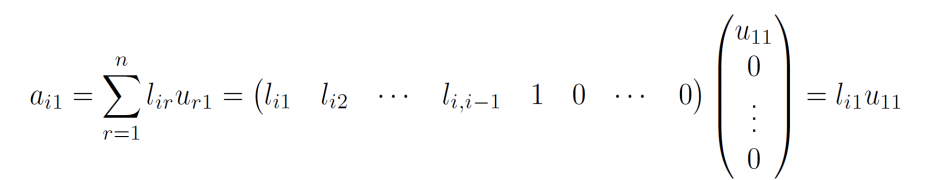
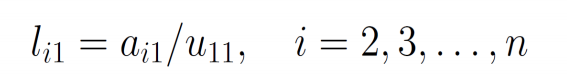
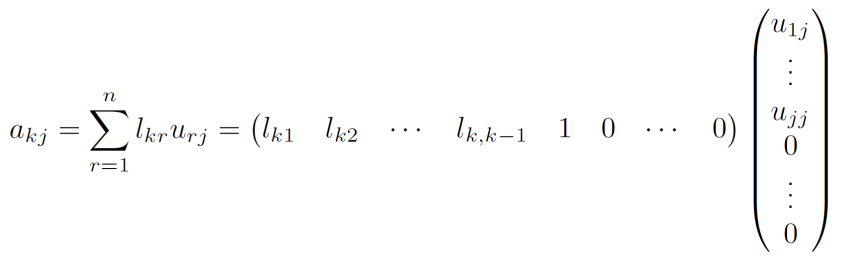
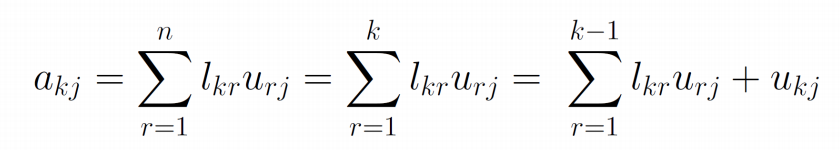

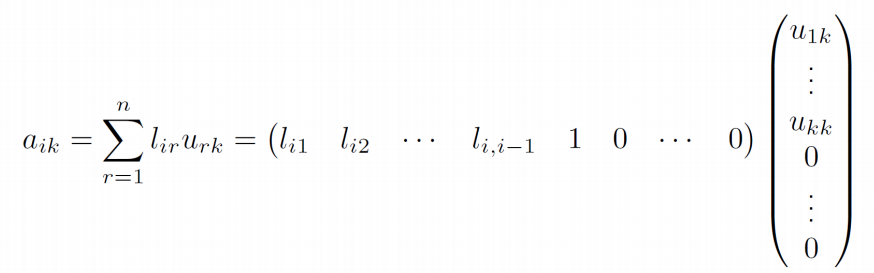
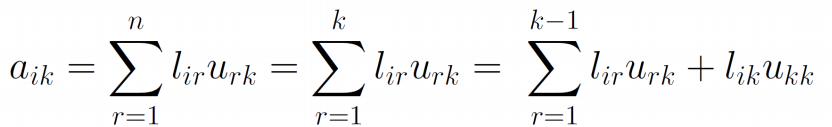
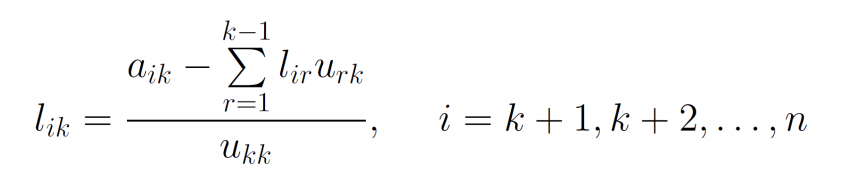
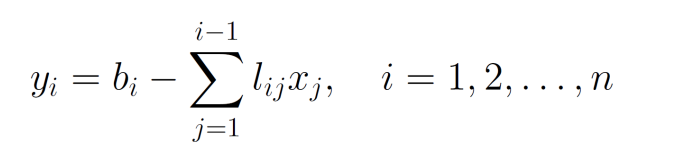
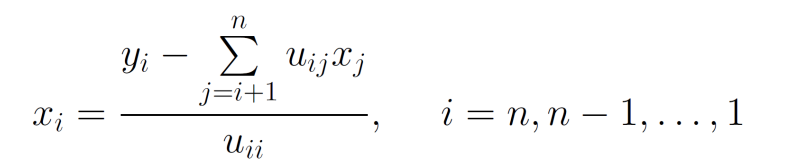
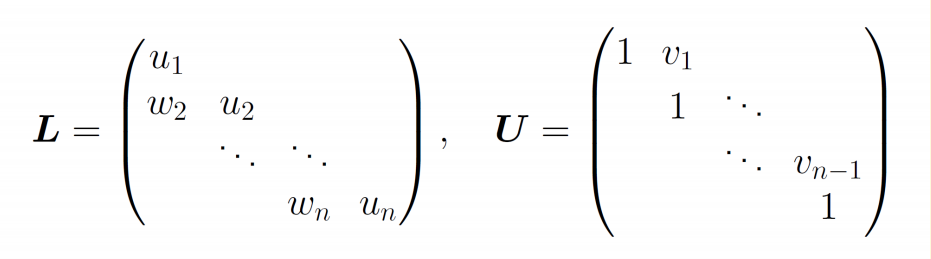
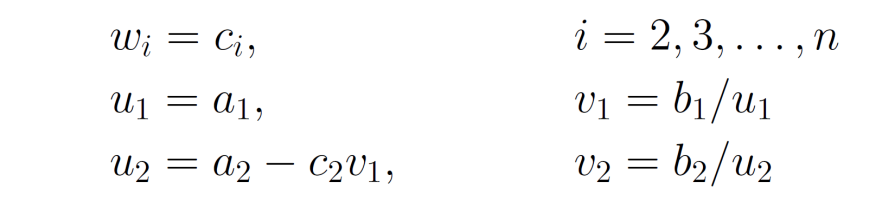
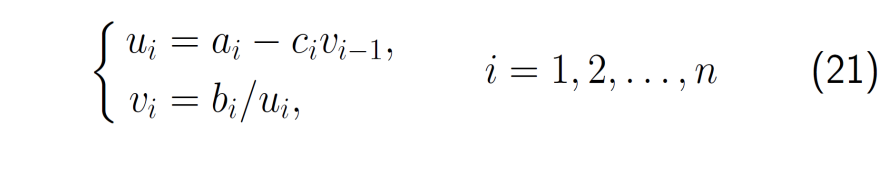
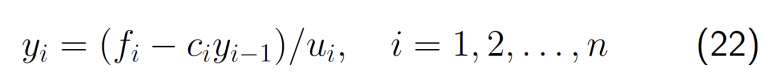
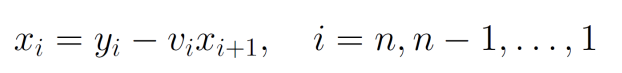
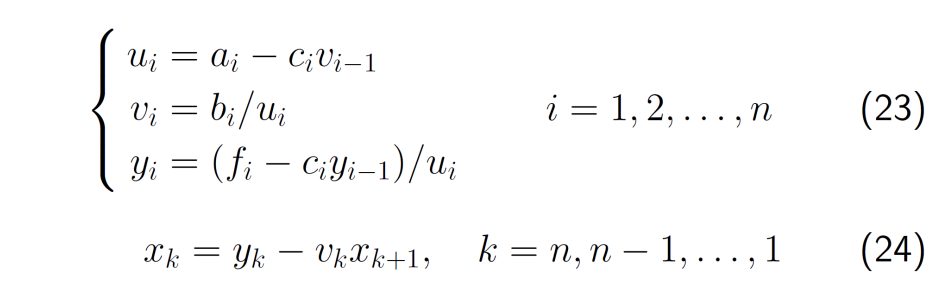


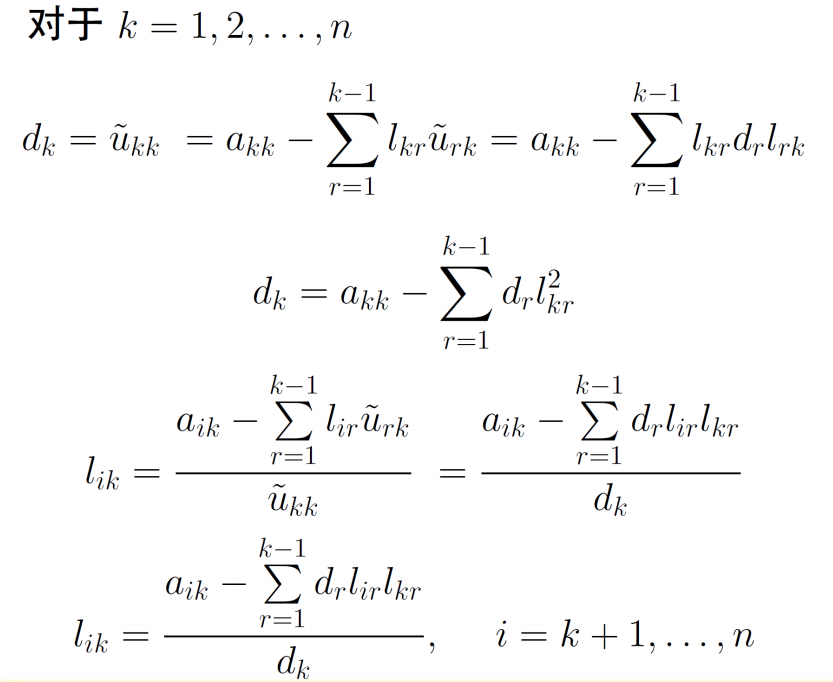






 浙公网安备 33010602011771号
浙公网安备 33010602011771号