上采样的几种方式

上采样：

在卷积神经网络中，由于输入图像通过卷积神经网络(CNN)提取特征后，输出的尺寸往往会变小

而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(如图像的语义分割)，这个使图像由小分辨率映射到大分辨率的操作，叫做上采样。

上采样的几种方法：

插值：
一、最近邻插值（Nearest Neighbor Interpolation）

对于未知位置，直接采用与它最邻近的像素点的值为其赋值

原图中（0，0）在放大后对应（0，0）

原图中（1，1）在放大后对应（4，4）

 

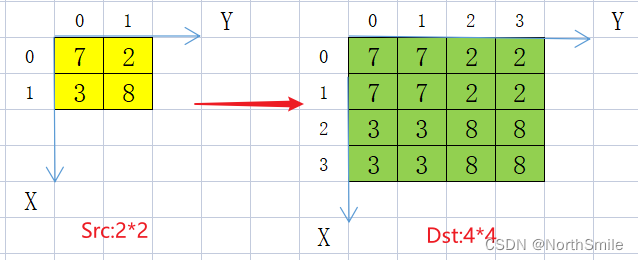
二、双线性插值（Bilinear Interpolation）

 

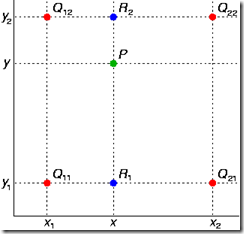
双线性插值就是做两次线性变换，先在X轴上做一次线性变换，求出每一行的R点：

 

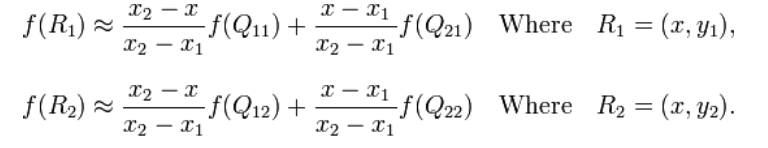
再通过一次线性变换求出在该区域中的P点：

可以把上式汇成所要计算的f（x,y）

 

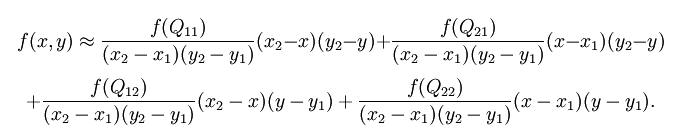
三、双三次插值（Bicubic Interpolation）

图中点（x,y）=(i+u,j+v)的值通过矩形网格中该点邻近的16个点加权平均得到。

假设源图像A大小为m*n，缩放K倍后的目标图像B的大小为M*N，即K=M/m。

A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一像素点(X,Y)的值，必须先找出像素(X,Y)在源图像A中对应的像素(x,y)，再根据源图像A距离像素(x,y)最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数，利用BiCubic基函数求出16个像素点的权重，图B像素(x,y)的值就等于16个像素点的加权叠加。

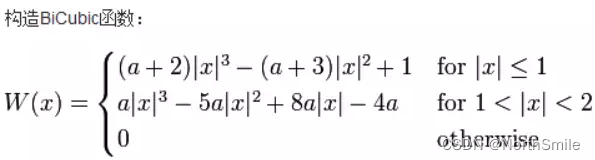
  根据比例关系x/X=m/M=1/K，我们可以得到B(X,Y)在A上的对应坐标为A(x,y)=A(X*(m/M),Y*(n/N))=A(X/K,Y/K)。

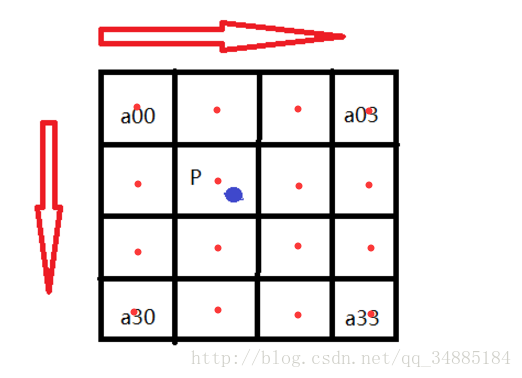
如图所示P点就是目标图像B在(X,Y)处对应于源图像A中的位置，P的坐标位置会出现小数部分，

所以我们假设 P的坐标为P(x+u,y+v)，其中x,y分别表示整数部分，u,v分别表示小数部分（蓝点到a11方格中红点的距离）。

那么我们就可以得到如图所示的最近16个像素的位置，在这里用a(i,j)(i,j=0,1,2,3)来表示，如上图。

 

 我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的权重W(x)。

BiCubic基函数是一维的，而像素是二维的，所以我们将像素点的行与列分开计算。

BiCubic函数中的参数x表示该像素点到P点的距离：

例如a00距离P(x+u,y+v)的距离为(1+u,1+v)，因此a00的横坐标权重i_0=W(1+u)，纵坐标权重j_0=W(1+v)，a00对B(X,Y)的贡献值为：（a00像素值）* i_0* j_0。

因此，a0X的横坐标权重分别为W(1+u)，W(u)，W(1-u)，W(2-u)；ay0的纵坐标权重分别为W(1+v)，W(v)，W(1-v)，W(2-v)；

B(X,Y)像素值为：

 

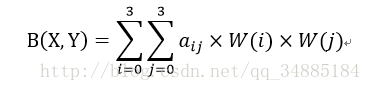
其实在插值计算时还可以使用矩阵表示，如下：

其中f(i+u,j+v)即为要计算的值，而A、C分别表示权重也就是第一种方式中的w_x,w_y，B为原图中16个邻近点构成的矩阵，计算权重的函数使用S(x)去近似。

 

源代码：

import torch
from torchvision import transforms
from PIL import Image
from torchvision.utils import  save_image


img=Image.open('./Jay.png',mode='r')
img_to_tensor=transforms.ToTensor()(img)
# print(img_to_tensor.shape)

nearest_neighbor_interpolation=transforms.Resize(size=(1024,1024),
                                       interpolation=transforms.InterpolationMode.NEAREST)
nearest_resize_img=nearest_neighbor_interpolation(img_to_tensor)

bilinear_interpolation=transforms.Resize(size=(1024,10248),
                                       interpolation=transforms.InterpolationMode.BILINEAR)
bilinear_resize_img=bilinear_interpolation(img_to_tensor)
#
bicubic_interpolation=transforms.Resize(size=(1024,1024),
                                       interpolation=transforms.InterpolationMode.BICUBIC)
bicubic_resize_img=bicubic_interpolation(img_to_tensor)

save_image(nearest_resize_img,'./nearest.png')
save_image(bilinear_resize_img,'./bilinear.png')
save_image(bicubic_resize_img,'./bicubic.png')

 

 

 特征金字塔相关补充知识：

对于深度卷积网络，从一个特征层卷积到另一个特征层，无论步长是1还是2还是更多，卷积核都要遍布整个图片进行卷积，大的目标所占的像素点比小目多，所以大的目标被经过卷积核的次数远比小的目标多，所以在下一个特征层里，会更多的反应大目标的特点。

特别是在步长大于等于2的情况下，大目标的特点更容易得到保留，小目标的特征点容易被跳过。

因此，经过很多层的卷积之后，小目标的特点会越来越少，越小越小。

其对特征点进行不断的下采样后，拥有了一堆具有高语义内容的特征层，然后重新进行上采样，使得特征层的长宽重新变大，用大size的feature map去检测小目标，当然不可以简单只上采样，因为这样上采样的结果对小目标的特征与信息也不明确了。

因此我们可以将下采样中，与上采样中长宽相同的特征层进行堆叠，这样可以保证小目标的特征与信息。

 

 

 

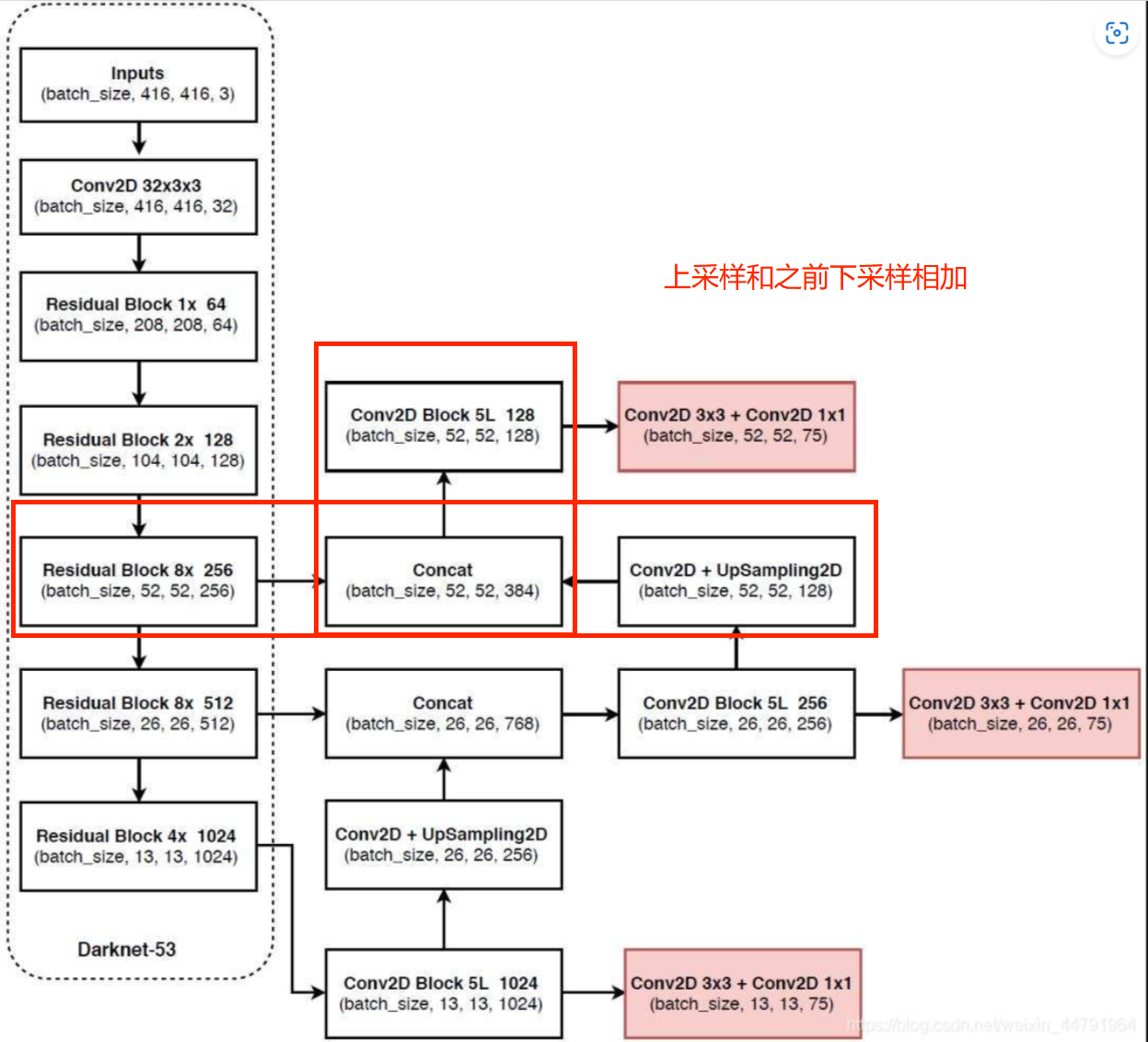
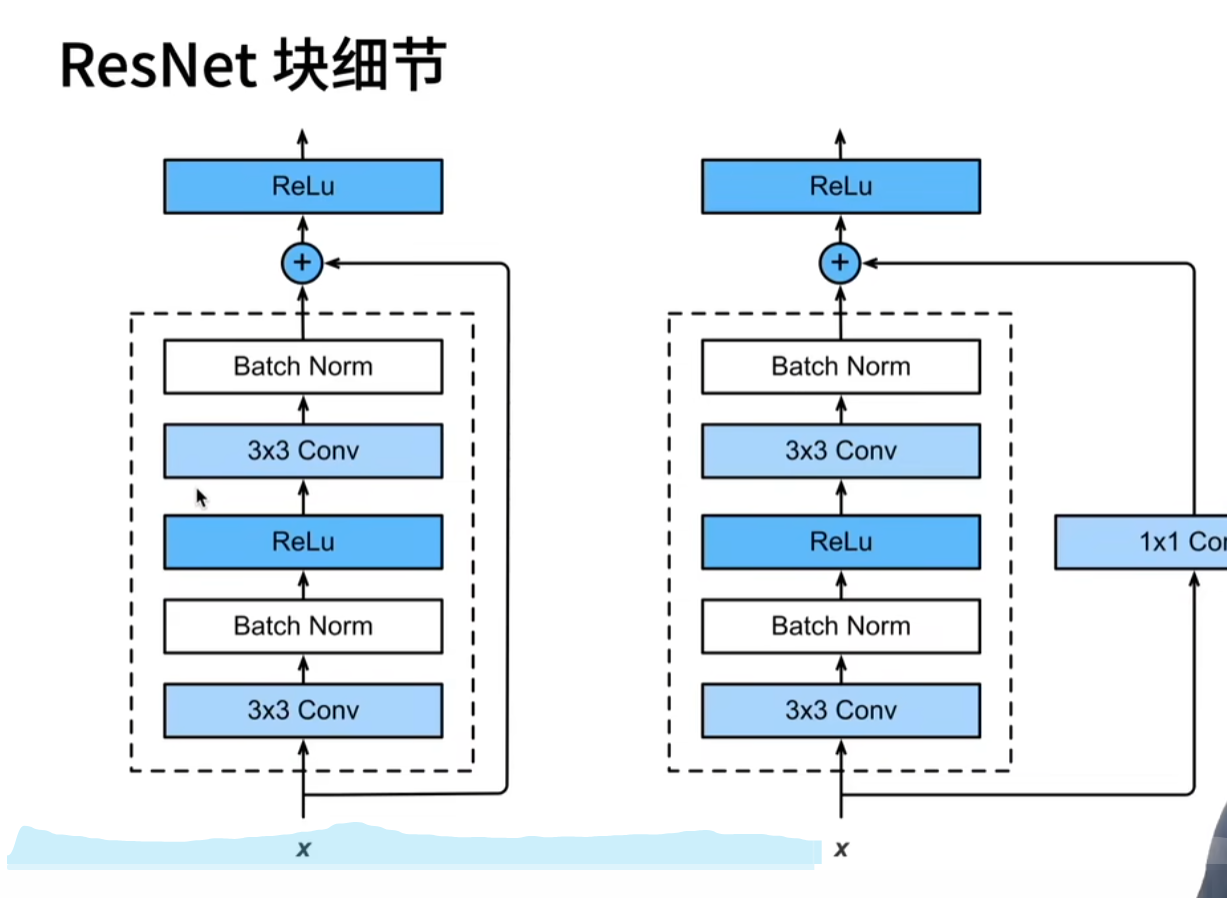
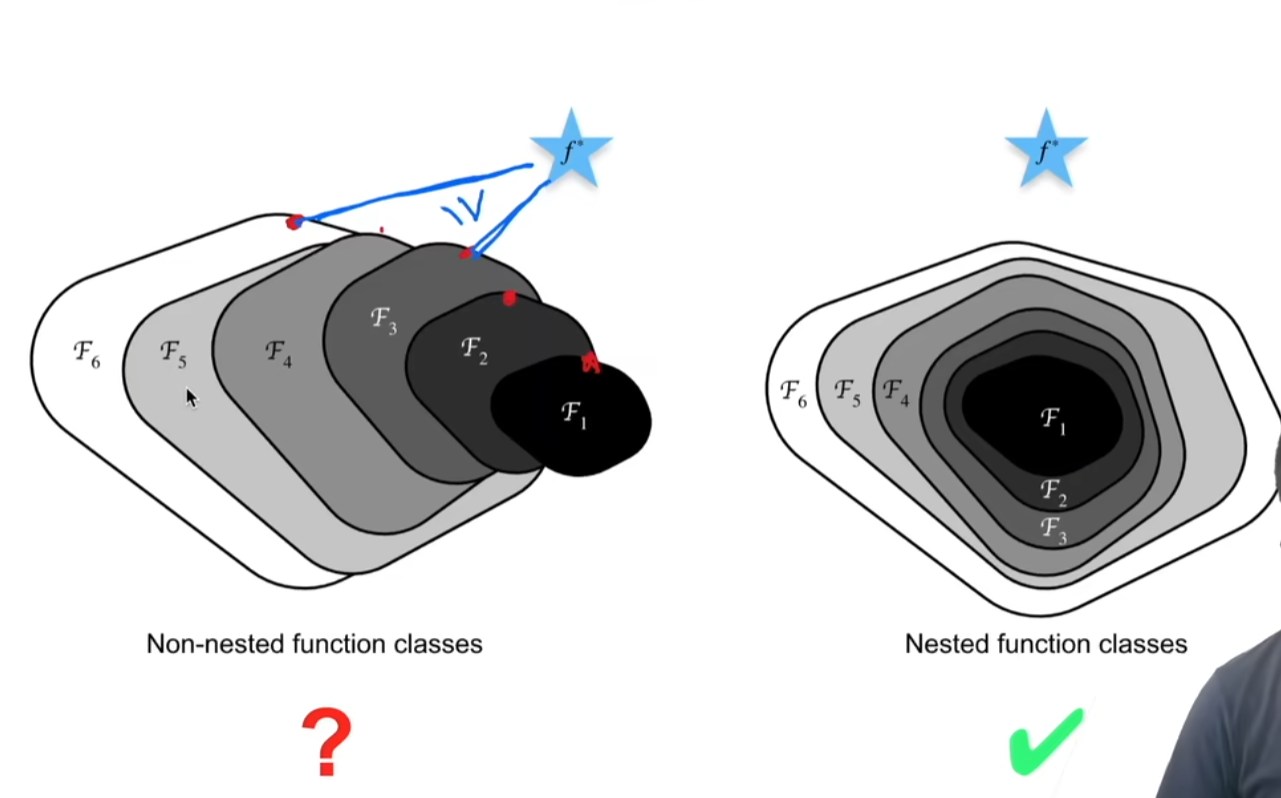
残差网络：