矩阵应用

经典题目6 给定n和p，求第n个Fibonacci数mod p的值，n不超过2^31
    根据前面的一些思路，现在我们需要构造一个2 x 2的矩阵，使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵，这两个数就会多迭代一次。那么，我们把这个2 x 2的矩阵自乘n次，再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想，这个2 x 2的矩阵很容易构造出来：
     　　

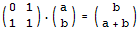
//矩阵乘法 +  矩阵快速幂 。。。求斐波拉契数 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>

typedef struct Matrix {
       int mt[10][10]; //存储矩阵值 
       int r, c; //存储矩阵维度 
}Mt;

int n, p;
//构造一个矩阵 
Matrix init_Matrix( Matrix A)
{      
       Matrix B = A; 
       B.r = 2;
       B.c = 2;
       for( int i = 0; i < B.r; i++)
            for( int j = 0; j < B.c; j++)
                B.mt[i][j] = 1;
       B.mt[0][0] = 0;
       return B;

}

//构造一个二维单位矩阵 
Matrix build_E_Matrix(Matrix C)
{
       C.r = 2;
       C.c = 2;
       C.mt[0][0] = 1, C.mt[0][1] = 0;
       C.mt[1][1] = 1, C.mt[1][0] = 0;
       return C;
}


 
 //矩阵相乘 
Matrix mul( Matrix A, Matrix B) 
{       
       Matrix C;
       C.r = A.r, C.c = B.c; // m * n * n * p = m * p;
       for( int i = 0; i < A.r; i++) {
            for( int j = 0; j < A.c; j++) {
                   int c = 0; 
                for ( int k = 0; k < B.c; k++) { 
                  c += A.mt[i][k] * B.mt[k][j] ;
                }
                   C.mt[i][j] = c ;
            }
       }
       return C;
}
               
//矩阵快速幂 
Matrix quickpow(Matrix A, Matrix C, int v)
{      
       Matrix B;
       B.r = 2;
       B.c = 1;
       B.mt[0][0] = 1;
       B.mt[1][0] = 1;
       while ( v ) {
             if ( v % 2 == 1 )
                  C =  mul(C, A);
             v = v / 2;
             A = mul(A, A);
       }
       C = mul(C, B);
       return C;
}
              
void print(Matrix A)
{
     for (int i = 0; i < A.r; i++) {
         for( int j = 0; j < A.c; j++) {
              printf("%d ", A.mt[i][j]);
         }
         puts("");
     }
}

int main( )
{
    int N;
    scanf("%d", &N);
    while( N-- ) {
           scanf("%d", &n); //求第几个斐波拉契数 
           Matrix A, B, C;
           A = init_Matrix(A);
           C = build_E_Matrix(C);
           B = quickpow(A, C, n);
           printf("%d\n",B.mt[1][0]);
    }
    return 0;
}