红黑树插入与删除操作的基本规则

刷题又久违刷到了红黑树的知识，才发现上次学完之后没有及时留下笔记，现在又回到了一知半解的状态。写技术笔记是多么重要啊（喝老鼠药.jpg），以下为这次学到知识的简单总结。

通俗来说

红黑树更像是一种有规则的“交通系统”，每个交叉口是一个节点，红色代表“警示”或“等待”的信号，黑色代表“通行”的信号。红色的交叉口不能连续，因为连续的等待会导致交通堵塞。所以，交叉口需要通过调控信号来保证交通的流畅和畅通，避免拥堵。这些规则确保了无论交通流量如何变化，整体的交通系统保持稳定高效。

更有网友云：左根右，根叶黑。不红红，黑路同。

红黑树基本规则

红黑树是一棵二叉查找树，即每个节点都有最多两个子节点的树。它的特点是每个节点都带有颜色（红色或黑色），通过特定的规则来保持树的平衡，确保操作（如插入、删除、查找）在最坏情况下的时间复杂度为O(log n)。

数值规则

• 左子树的值<父节点的值<右子树的值

这意味着，红黑树和普通的二叉查找树一样，节点的顺序是有要求的。

颜色规则

• 根节点为黑色
• 叶节点(NIL)为黑色
• 红节点的子节点必为黑色：不能出现两个连续的红节点
• 任何点到其可达叶节点的路径上，都经过相同数量的黑节点

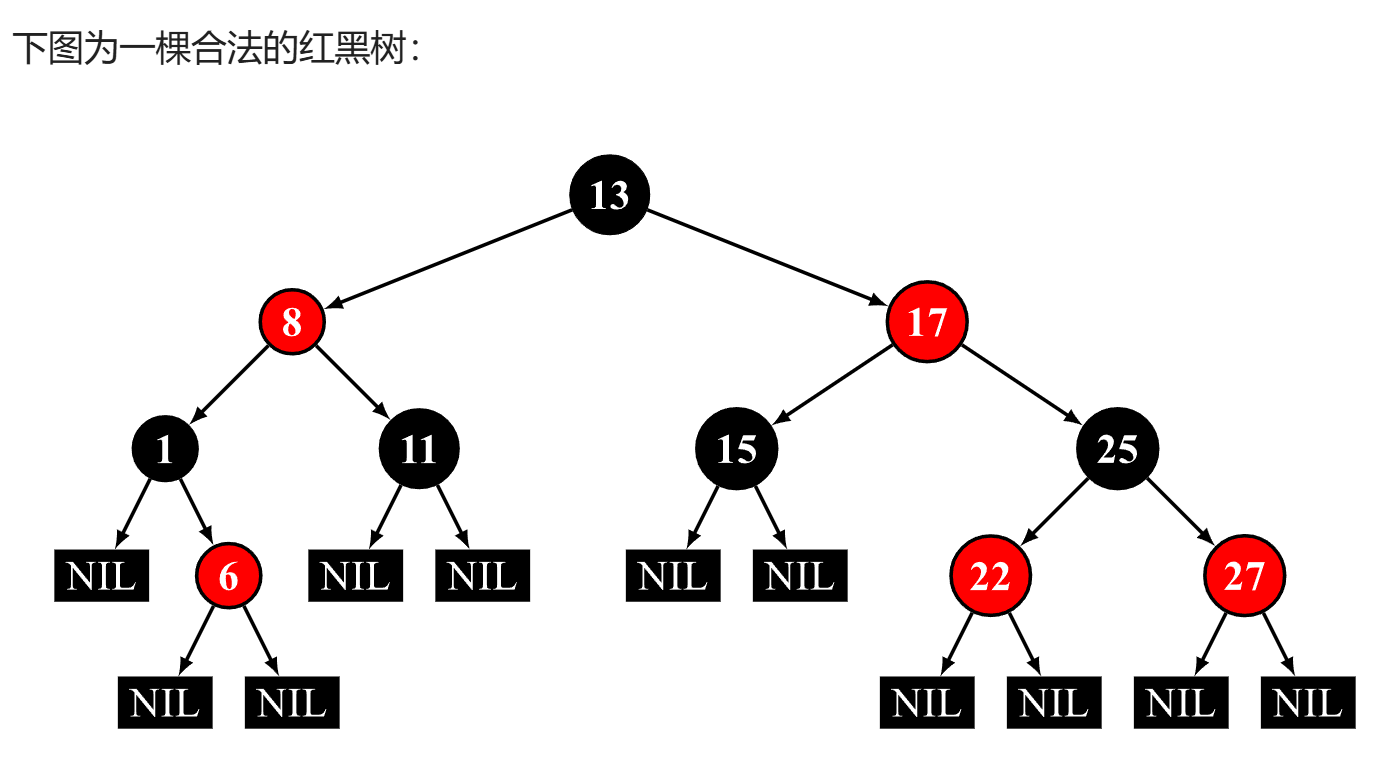
平衡规则

	平衡因子	优点
AVL树	任一节点左右子树高度差绝对值不超过1	查询更高效
红黑树	任一节点左右子树高度差不超过2倍	频繁插入和删除更高效

• 插入操作

  默认插入节点为红时，讨论cur节点在以下位置的情况

  • 根节点：翻黑色

  • uncle节点为红：翻色

    uncle/father/grandf翻色，往上递归判定grandf的uncle/father是否合法；
    

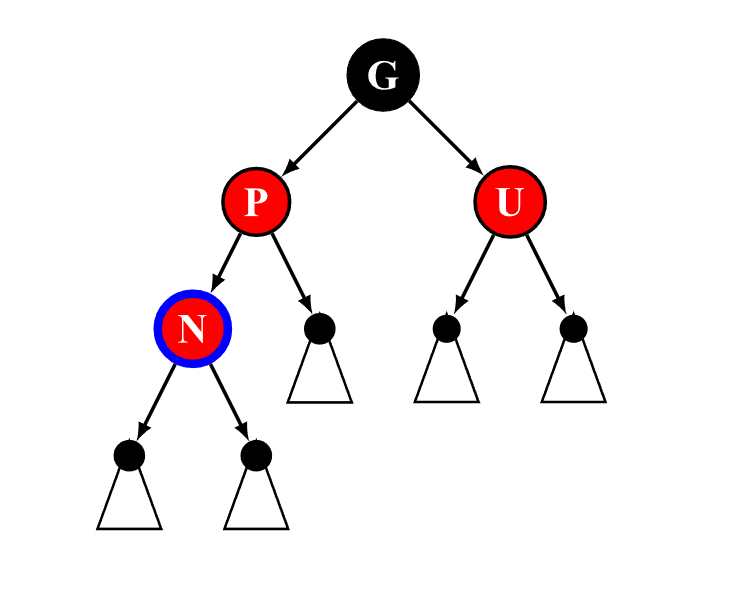
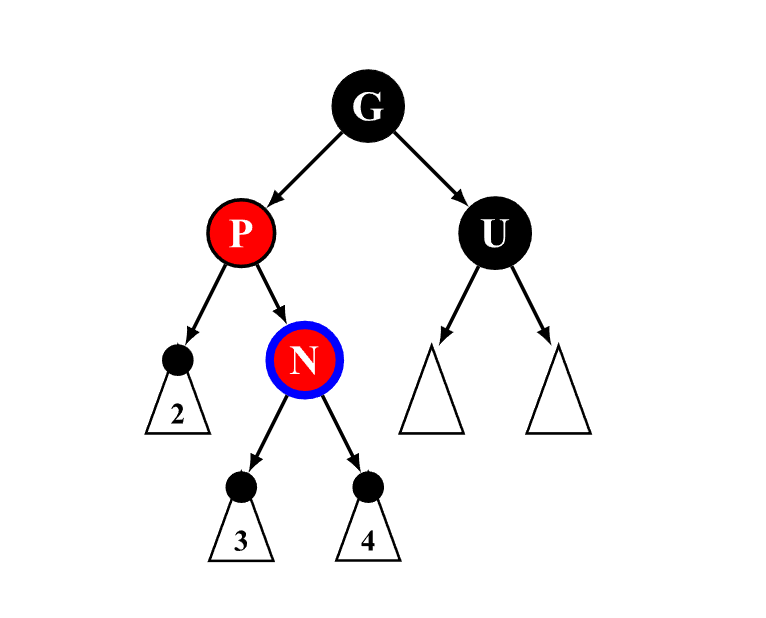
  • uncle节点为黑：旋转后翻色

    • LL型

      father为根，grandf右旋--翻色

    • RR型

      father为根，grandf左旋--翻色

    • LR型

      cur为根，father左旋，grandf右旋--翻色
      

    • RL型

      cur为根，father左旋，grandf右旋--翻色

• 删除操作

举例

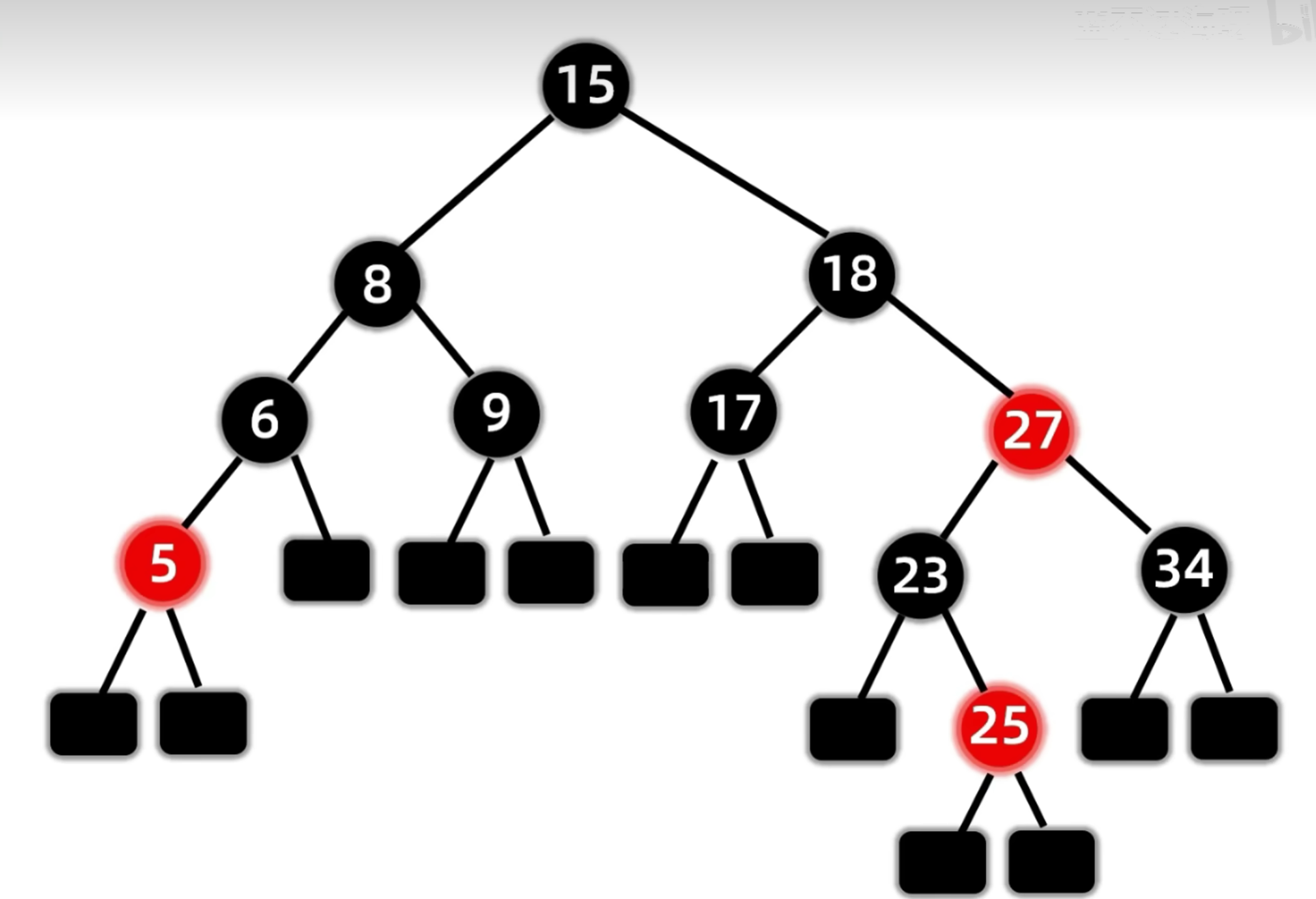
插入：17 18 23 34 27 15 9 6 8 5 25。转换为红黑树后如图：

友情链接

B站--红黑树动画演示

OIWIKI--数据结构：红黑树