【阅读笔记】《数学之美》（一）图论部分

9.图论和网络爬虫

9.1 欧拉七桥问题

能否将下图中的每座桥恰好走过一遍并回到出发点：

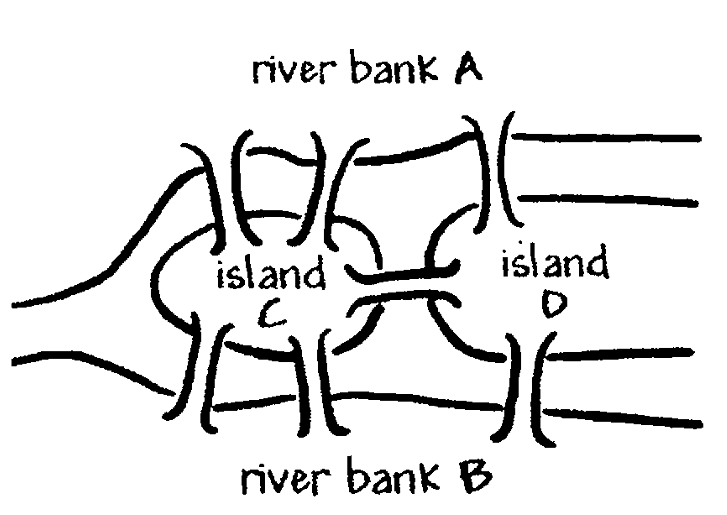
不能。

将每一块连通的陆地抽象为一个顶点，每一座桥当成图的一条边，则上图可简化为：

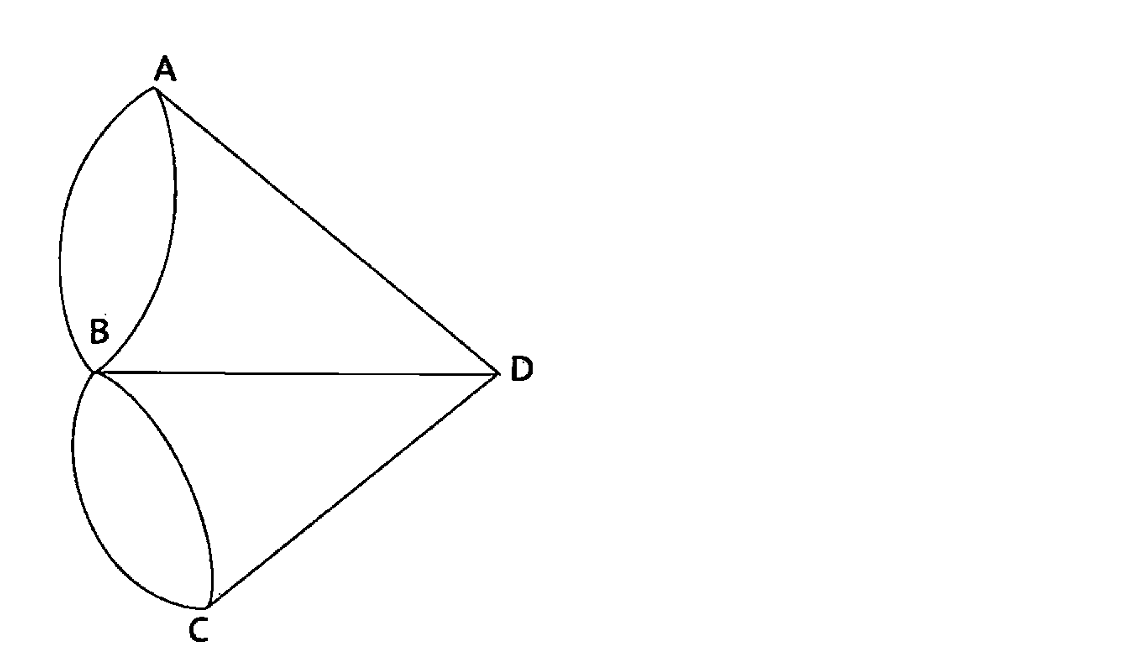
每一个顶点，其相连的边的数量定义为它的度（degree）。

定理：如果一个图能够从一个顶点出发，每条边不重复的遍历一遍回到该顶点，那么每一顶点的度必须为偶数。

证明：若能遍历图的每一条边各一次，那么对每个顶点，需要从某条边进入顶点，同时从另一条边离开这个顶点。进入和离开顶点的次数是相同的，因此每个顶点有多少条入边，就有多少条出边。换句话说，每个顶点相连的边的数量是成对出现的，即每个顶点的度都是偶数。

在七桥问题中，多个顶点的度为奇数，因此，这个图无法从一个顶点出发，遍历每条边各一次再回到这个顶点。

9.2 如何构建网络爬虫

在超链接的基础上，从任何一个网页出发，用图的遍历算法，自动的访问到每一个网页并存储，完成这个功能的程序即为网络爬虫（某些文献中称为“机器人”）。

构建网络爬虫有三个关键问题：

1. BFS or DFS

   • 假设不考虑时间因素、互联网静态不变，二者都能在大致相同的时间里“爬下”整个“静态”互联网上的内容
   • 但在现实中，搜索引擎的网络爬虫问题更应定义为——如何在有限时间里最多的爬下最重要的网页
   • 最重要的网页应该是首页，如果把爬虫再扩大些，应爬下与首页直接链接的网页
   • 因此，BFS明显优于DFS
   • DFS的使用情况需要考虑爬虫的分布式结构，以及网络通信的握手成本

2. 页面的分析和URL的提取

   • 早期互联网用HTML语言书写网页，前后都有明显的标识，可直接提取
   • 现在很多网页用脚本语言（e.g.JavaScript）生成，URL是运行一段脚本之后得到的结果
   • 分析页面需要模拟一个浏览器运行一个网页，才能得到隐含的URL
   • 但考虑到网页能在浏览器中打开，说明浏览器可以解析，做浏览器内核的工程师来写网络爬虫中的解析程序，能有效的解析网页的脚本

3. 记录哪些网页已经下载过的小本本--URL表

   • 用哈希表来记录已下载的URL

   • 在一台下载服务器上建立、维护一张哈希表不是难事，但同时有上千台服务器一起下载网页，维护一张统一的哈希表可能会出现问题（容量问题，通信问题）

   • 针对通信问题，好的解决办法一般采用这两种技术：

     • 明确每台下载服务器负责的URL类别，避免多台服务器对同一个URL的下载判断
     • 在明确分工的基础上，批处理判断是否下载该URL
     • 这样即可大大减少通信次数

9.3 小结

• 下载网页到服务器（网络爬虫）只是搜索引擎建立索引前的步骤，基于离散数学中的图论原理
• 如何构建网络爬虫是很能考察工程素养的一道面试题，它的答案没有完全的对错，但是有好与不好、可行和不可行的答案，也需要考虑非常多工程上实现的细节，需要好好思考

10.PageRank————民主表决式网页排名技术

最先试图给网站排序的不是谷歌，而是雅虎，他们尝试使用目录分类的方式让用户通过互联网检索信息，但收录网页量有限，而且只能对常见用词进行索引。

后来DEC开发了AltaVista，只用了一台Alpha服务器就收录大量网页，并且能对每个词都进行索引，有效的解决了覆盖率问题。尽管AltaVista能给出大量结果，但大部分结果与查询本身不太相关。

直到谷歌提出的PageRank技术，提升了网页内容与查询的相关度。

10.1 PageRank算法原理

简单来说就是民主表决：

• 网页之间的投票
  • 每个网页都是一个节点，而网页之间的链接就像是一种“投票”
  • 网页A链接到网页B时，可以看作是A对B投了一票
  • 表明A认为B是重要的
• 投票权重
  • 并不是所有的投票都具有相同的权重
  • 一个PageRank值很高的网页投出的票比一个PageRank值很低的网页投出的票更有价值
  • 权威的网页的“推荐”更能影响其他网页的排名
• 迭代计算
  • PageRank算法通过不断迭代计算，最终为每个网页分配一个0到1之间的PageRank值
  • 这个值越高，说明该网页越重要

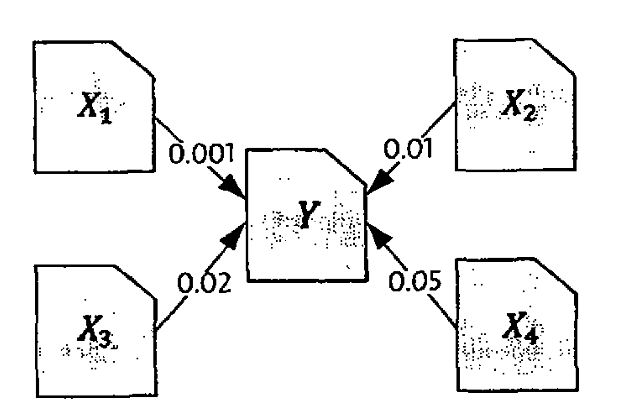
10.2 PageRank计算方法

主要是矩阵相乘，这种计算很容易分解成许多小任务，在多台计算机上并行。

10.3 小结

• PageRank算法看起来复杂，但其核心思想非常直观：一个网页的重要性取决于指向它的链接的数量和质量

11.确定网页与查询的相关性

11.1 TF-IDF

搜索关键词的科学度量：

• Term Frequency（单文本词频）
  • 各关键词\(w\)在\(D_w\)个网页中出现的总词频
• Inverse Document Frequency（逆文本频率指数）
  • \(log( \cfrac DD_w)\)
  • 考虑到停止词和专业词汇应该分配不同权重
  • 停止词权重=0
  • TF越小，越专业，权重越大

11.2 小结

• TF-IDF = TF * IDF
• 是一种用于信息检索与文本挖掘的常用加权技术
• 它通过统计一个词语在文档中出现的频率（TF）以及该词语在整个语料库中出现的频率（IDF），来评估该词语对于一个文档的重要程度

12.有限状态机、动态规划（地图和本地搜索的最基本技术）

地图服务的流量与网页搜索相比，只是众多垂直搜索的一部分。

智能手机的定位和导航功能，关键技术有三：

• 利用卫星定位

• 地址识别——有限状态机

• 根据用户输入的始终点规划最短/快路线——动态规划

12.1 地址分析

在地址描述不规范的情况下，人类可以确定准确地址，但机器很难准确的提炼出相应的地理信息。根本原因在于，地址描述看上去简单，但仍是比较复杂的上下文相关的文法，而非上下文无关。

对此，最有效的识别和分析地址的方法，是有限状态机。

12.2 有限状态机

（Finite State Machine，FSM）
是一个特殊的有向图，包括状态（节点）和连接状态的有向弧

数学定义为一个五元组（\(\Sigma\), \(S\), \(s_0\), \(\delta\), \(f\) ） ：

元素	描述
\(\Sigma\)	输入符号
\(S\)	非空的状态节点
\(s_0\)	起始状态
\(\delta\)	\(S\times\Sigma\rightarrow S\)
\(f\)	终止状态

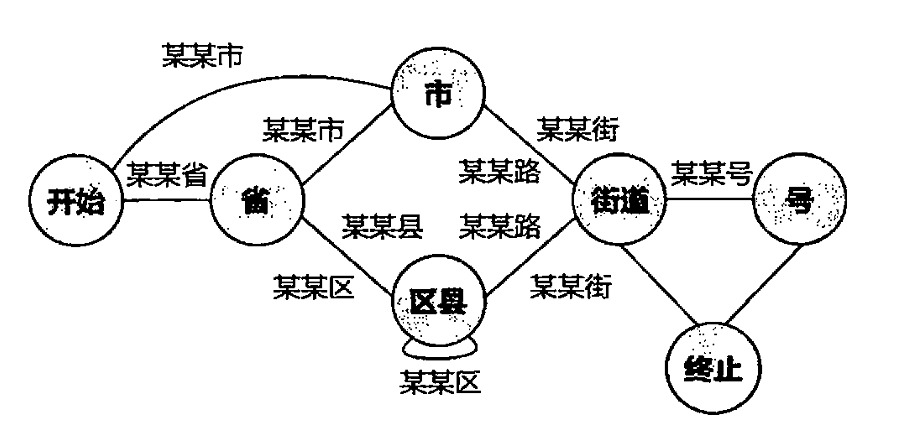
使用有限状态机识别地址，有两个关键问题（目前已有现成算法）：

• 通过有效的地址建立状态机
• 地址字串的匹配算法
  • 有了有限状态机之后，用它分析网页
  • 找出网页的地质部份，建立本地搜索的数据库
  • 同样也可以分析用户输入的查询，挑出描述地址部分

有限状态机只能进行严格匹配，所以对于自然语言的随意性和错别字问题，显得效率极低。如果可以实现模糊匹配，地址识别的准确性将大幅提升。

因此，科学家们提出了基于概率的有限状态机，基本等效于离散的马尔科夫链。

12.3 全球导航与动态规划

所有的导航系统都是用的动态规划的办法，这里面的programming一词在数学上的含义是“规划”，不是计算机里的“编程”。

具体步骤为：

• 从起点开始，逐步计算到达其他节点的最短路径长度。
• 利用状态转移方程，根据已计算出的子问题的解，计算当前状态的解。
• 为了避免重复计算，可以采用记忆化搜索或自底向上的迭代方法。
• 从终点开始，根据动态规划表中的信息，逐步回溯，找到最短路径。

此外，不得不提动规和贪心的区别：

特点	动态规划	贪心
核心思想	最优子结构，重叠子问题	贪心选择性质
解决问题方式	自底向上，逐步求解子问题	自顶向下，逐次做出贪心选择
时间复杂度	一般较高，但能保证最优解	一般较低，但不能保证最优解
适用范围	具有最优子结构和重叠子问题的优化问题	具有贪心选择性质的问题

12.4 有限状态传感器

FSM在语音识别和自然语言理解领域调整为一种特殊的有限状态机————加权的有限状态传感器WFST：每个状态由输入和输出符号定义

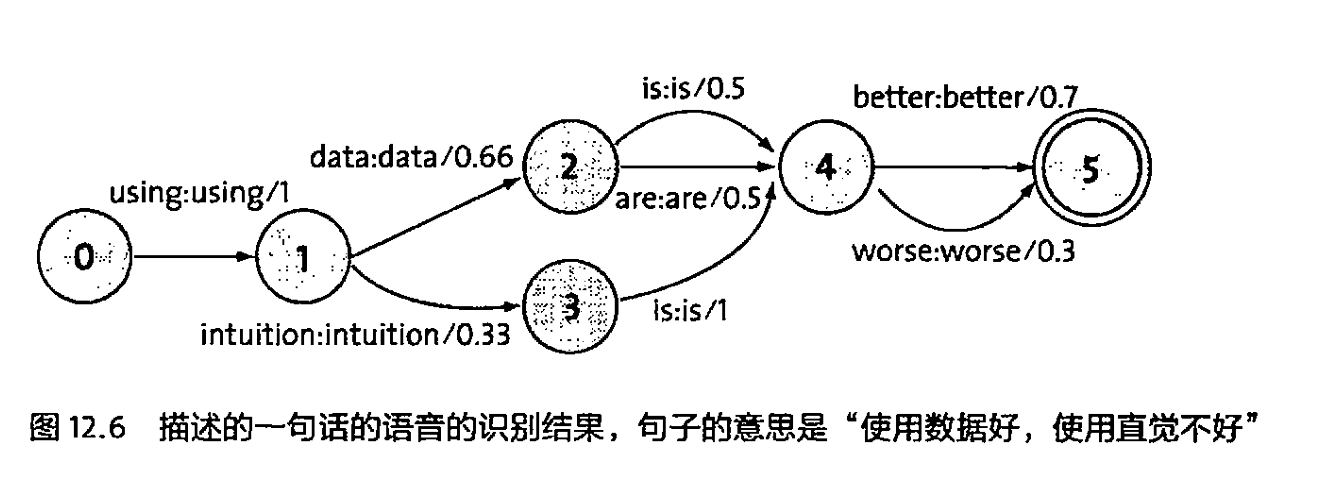
算法原理基于动态规划，WFST中的每一条路径就是一个候选的句子，概率最大的路径则为该句子的识别结果。

12.5 小结

• 有限状态机（FSM）可以简单粗暴的理解成：特定状态节点下的有向图
• 使用FSM进行地址识别，是因为他能有效的结构化解析地址
• 动规是路径规划问题中寻优路径的最佳选择
• 在语音识别和NLP领域，FSM扩展为WFST
  • 因其任何一个节点的前后二元组，都能对应一个状态，WFST也是天然的NLP分析、解码工具