【小题狂练B】“堆砌的书本纸张失去了它们应有的意义 回想一天的场景辗转恐惧天明”

P2290 [HNOI2004] 树的计数

一眼 prufer 序列板子题，我们考虑相当于在长度为 \(n-2\) 的序列中填 \(n\) 个数，每个数可以出现 \(a_i-1\) 次，根据可重集的组合数，答案为 \(\frac{(n-2)!}{\prod\limits_{i=1}^{n}(a_i-1)}\)，但是这道题不取模很坏，预处理组合数暴力做，复杂度 \(O(n^2)\)。

P1715 [USACO16DEC] Lots of Triangles P

萌萌计几题，但是往面积想于是倒闭了。

点击查看图片

对于一个这样的三角形，我们先把形成的这个直角梯形里头包含的点算出来，然后容斥一下去掉下面两个的直角梯形内部的点，然后就能直接做了。

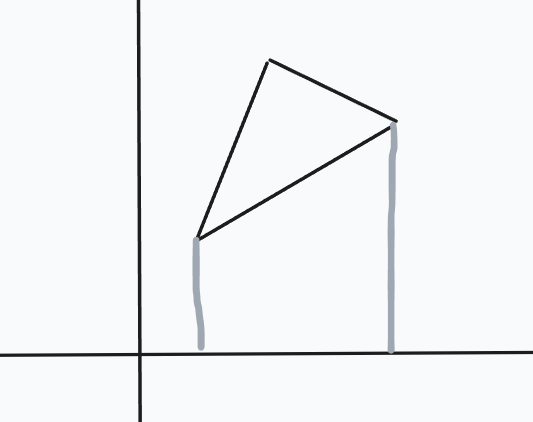
对于这样的三角形和上面的同理，直接把底下的直角梯形内部包含的点算出来然后容斥即可。

P6162 [Cnoi2020] 四角链

很容易想到一个 \(dp_{i,j}=(i-j+1)dp_{i-1,j-1}+dp_{i,j-1}\)，其中 \(dp_{i,j}\) 表示前 \(j\) 个已经填了 \(i\) 个的方案数。

这个，长得很像斯特林数吧，所以推一下，发现是一个 \({n\brace n-k}\) 的形式，直接算即可。

P2182 翻硬币

我们考虑对于一个硬币如何才是正确的情况，很简单，就是被翻了偶数次。朴素的想法就是 \(dp_{i,j}\) 表示翻转 \(i\) 次有 \(j\) 个相同的方案数，我们假设我们一次操作翻了 \(x\) 个同方向硬币 \(y\) 个反向硬币，可以知道 \(x+y=m\)，假设我们上一个状态是 \(k\)，那么 \(k-x+y=j\)。那么我们就知道 \(dp_{i,j}=\sum_k dp_{i-1,k}\binom{\frac{m-j+k}{2}}{k}\binom{\frac{m+j-k}{2}}{n-k}\)，复杂度 \(O(n^2k)\)

P2714 四元组统计

容易想到对于 \(\gcd(a_i,a_j,a_k,a_l)=1\) 的个数，我们可以转化为 \(\gcd(a_i,a_j,a_k,a_l)\not = 1\) 的个数然后用 \(\binom{n}{4}\) 减去 \(\sum_i\sum_j\sum_k\sum_l{[\gcd(a_i,a_j,a_k,a_l)\not = 1]}\)，这个显然比较菜，我们可以考虑分解质因数，假设我们现在选取的答案是 \(v\)，对应的包含这个因数的个数是 \(m_v\)，那么我们这一部分的答案就是 \(\binom{m_v}{4}\)，但是有重复的，我们考虑倒着算，然后算新的的时候把旧的减去 \(ans_{i}=\binom{m_i}{4}-\sum_{j=2}^{\frac{maxn}{i}}ans_{j\times i}\)。

P5596 【XR-4】题

这题怎么看起来这么典。

考虑转化，原式等于 \(y^2-ax-x^2+b=0\)，再进行一步变换也就是 \(y^2+\frac{a^2-4b}{4}=(x+\frac{a}{2})^2\)。这个显然很菜啊，我们把右边的移动到左边发现是一个平方差。\((y-x-\frac{a}{2})(y+x+\frac{a}{2})=\frac{4b-a^2}{4}\)。两边同时乘上 \(4\) 化一下，变成 \((2y-2x-a)(2y+2x+a)=4b-a^2\)。右侧我们可以直接计算，左侧我们尝试暴力枚举因数，然后判断即可。

P4921 [MtOI2018] 情侣？给我烧了！

我们考虑先求出来坐 \(k\) 对情侣是啥情况，显然是一个 \(\binom{n}{k}^2\times k!\times 2^k\) 的形式，我们设 \(f_i\) 表示 \(i\) 对情侣不坐在一排的方案数，那么答案就是 \(ans_{n,k}=f_i\times (n-k)! \times 2^{n-k} \times \binom{n}{k}^2\times k!\times 2^k\)。我们现在考虑如何计算这个 \(f_i\)。

根据题目提示，我们想到一个容斥：用所有数量减去所有存在和睦的人数，剩下的就是不和睦的人数。也就是 \(f_n=2^n-\sum_{i=1}^{n} ans_{n,i}\)。

P4345 [SHOI2015] 超能粒子炮·改

欧耶香香软软的小模数我们都很喜欢你。

我们考虑我们要求的是 \(\sum_{i=1}^{k} \binom{n}{i}\)，设这个是 \(f_{n,k}\)，稍微化简一下，\(\sum_{i=1}^{k} \binom{n}{i}=\sum_{i=1}^k\binom{\lfloor n/p \rfloor}{\lfloor i/p\rfloor}\binom{n \bmod p}{i \bmod p}=\sum_{x=0}^{p-1}\binom{n \bmod p}{x}\sum_{i=0}^{k}[i \bmod p=x]\binom{\lfloor n/p \rfloor}{\lfloor i/p\rfloor}\)。
然后类似莫反时候的做法，我也不知道该叫什么。\(\sum_{x=0}^{p-1}\binom{n \bmod p}{x}\sum_{i=0}^{k}[i \bmod p=x]\binom{\lfloor n/p \rfloor}{\lfloor i/p\rfloor}=\sum_{x=0}^{p-1}\binom{n \bmod p}{x}\sum_{i=0}^{\frac{k-x}{p}}\binom{\lfloor n/p\rfloor}{i}=\sum_{x=0}^{p-1}\binom{n \bmod p}{x}f_{\frac{n}{p},\frac{k-x}{p}}\)

前面的太菜了，可以预处理前缀和。

P4430 小猴打架

显然的 prufer 序列板子，相当于在 \(n-2\) 个位置填 \(n\) 个可以相同的数，然后每个生成树有 \((n-1)!\) 种生成方式，答案也就是 \((n-1)!n^{n-2}\)

P3414 SAC#1 - 组合数

低能粒子炮。答案显然是 \(2^{n-1}\)

P4981 父子

容易想到这个是一个类似树的形式的，相当于求一个完全图的生成树（有根）个数，答案就是 \(n^{n-1}\)。

P2675 《瞿葩的数字游戏》T3-三角圣地

这个题好诡异。

我们容易想到肯定要把比较大的放在尽可能中间，这样就会多产生一点贡献。对于位置 \(i\)，其对底部的贡献是 \(\binom{n-1}{i-1}\)，然后卢卡斯暴力计算即可。

P2490 [SDOI2011] 黑白棋

考虑什么情况下小 A 先手必然获胜。