一些 NOIP 前复习
11.19
我草我草怎么只剩下 10 天了呜呜呜呜呜呜呜呜不要不要不要这种事情绝对不要呜啊。
建树，考虑对于建出来的树在上面进行一个类似归并排序的状态可以直接做。
欧几里得距离是 \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)，我们考虑这题看起来就比较 dp。
我们设一个 \(dp_{i,j,S}\) 表示选取第 \(i\) 列，已经选取了 \(j\) 个，\(S\) 表示状态。抛掉一个都不选的状态，我们有 \(7\) 种状态，我们枚举下一列和选择情况即可。
考虑对于每个城市爆炸的概率都是 \(\dfrac{1}{n}\)，不被选中的概率是 \(\dfrac{n-1}{n}\)。容易想到我们递推求解，设 \(E_i(x)\) 表示第 \(x\) 天后城市 \(i\) 威力的期望，对于第 \(k\) 天的城市 \(i\)，有两种可能。被选中爆炸，概率为 \(\dfrac{1}{n}\)，城市 \(i\) 的威力变为 \(0\)，其他城市增加 \(\dfrac{E_i(k-1)}{n}\)。没有被选中爆炸，概率为 \(\dfrac{n-1}{n}\)，第 \(i\) 个城市变为 \(\dfrac{E_{被选中的城市}(k-1)}{n-1}+E_i(k-1)\)。
我们可以比较容易的计算出来了吧，我们定义一个 \(S=\sum_{i=1}^na_i\)。
我们发现复杂度为 \(O(nk)\) 的不是很能过，考虑递归化简。
直接做即可。
邪恶题，我们考虑只有一整个从 \(0\) 开始连续的自然数才是有用的。如果对于一个 \(i\)，它的个数比 \(i-1\) 还要多，那么多出来的部分也是没有用的，可以直接求 \(\min\)，容易发现这会是一个单调不升的状态。
我们对于给定的 \((a_i,b_i)\) 进行按照 \(a_i\) 从小到大排序，排序后对于 \(b_i\) 和前面的其他 \(b_i\) 进行求最小值，我们就可以直接维护算出所能求出的 \(\text{mex}\) 总和的最大值。
考虑长度固定，我们二分答案 \(u\) 枚举序列判断大于等于 \(u\) 的数的个数计算能否成立即可，我们的长度是固定的所以可以直接枚举起始点。
11.20
容易发现 \(a\) 是 \(n\) 的因数，我们枚举因数 \(a\)，剩下的就是 \(1+p+pq = \frac{n}{a}\)，然后枚举 \(\frac{n}{a}-1\) 因数即可。
考虑我们往前走 \(x\) 和往前走 \(y\) 步再回头走到 \(x\) 都能走 \(x\)，那么我们考虑建图算出来往前走 \(i\) 格的最小花费。
我们尝试进行 \(dp\)，定义一个 \(f_{i}\) 表示到 \(i\) 需要的最小花费，转移方程为 \(f_i=\min\limits_{j=1}^{i-1}\{\max(f_j,f_{i-j})+dis_{j}\}\)。
最开始以为是直线读错题了。
发现有 \(n\) 个颜色和 \(n+1\) 个点，于是注意到不会有交点，只需要考虑怎么构造即可。
我们发现可以拍到一维来做，因为一维上构造是好做的，注意到二维上没有重点，如果投影后都不交显然是不交的。我们每次选出来最短的，里头最多只会让每种颜色去掉一个，所以成立。
我们考虑只有两组，我们对第一组排序，然后用第二维做第二关键字。然后我们对于每个排序后的求 \(\max\)，因为较大者必然产生贡献。
然后我们对于较小者跑一个 LIS 即可。
我草这题是啥，有一个 20 位数位 dp 做法但是好像比较邪恶，所以来朴素的。
我们考虑先对 \(k\) 进行质因数分解，这个是比较显然的。分解之后只会有若干个 \(2,3,5,7\) 和一些比 \(10\) 还大的质数。因为我们能且只能选 \(0\sim9\) 的数作为位数，所以遇到比 \(10\) 还大的数就只能选 \(0\) 了，没有比 \(0\) 大的就可以考虑往里头填 \(2,3,5,7\)，对于填 \(4\) 和 \(8\) 当做填多个 \(2\)，\(9\) 也是同理。
我们发现最多填 \(60\) 个 \(2\)，\(40\) 个 \(3\)，其他的都是 \(20\) 个，暴力枚举即可。
11.21
- P3435 [POI 2006] OKR-Periods of Words
我们对于一个字符串 \(S\) 和前缀 \(s\)，判断字符串 \(S\) 是不是 \(ss\) 的前缀就是判断 \(S_{|s| \sim len}\) 是否和 \(s\) 中这段的对应是否相等即可。
我们枚举暴力判断的复杂度是 \(O(n^2)\) 的，显然没法过，因为具有单调性所以我们考虑进行二分查找。暴力统计答案即可。
- P9149 串串题
开题想到考虑每次枚举删除的数，然后把这些形成的串中间拼起来成一个串跑一遍出现次数。复杂度 \(O(n\binom{W}{d})\)，显然过不去考虑优化。
我们考虑到所有有可能产生影响的数是一定不能选的，这里很显然。我们先把 A 中所有不可以选的全部拉出来，然后枚举左端点跑子串 Hash 求出可以提出来 B 的子串位置。我们发现我们其实需要的只是权值和，这个可以拆成每个序列出现的次数，所以并不互相影响，直接计算即可。
11.23
- P14098 [POCamp 2022] 狼抓兔子 II / Djur
邪恶题目。我们考虑题目是需要求出两条从 \((1,1)\) 到 \((n,m)\) 不交的路线，答案是一个尽可能往左走一个尽可能往右走，这样构造出来的一定是成立且不交的，想起来很自然但是我不会证。不过我们发现，其实可以直接网络流。
11.24
- P14125 [SCCPC 2021] Monster Hunter
读错题了没看到 \(a_i\) 小于等于 \(3\)。
显然二分答案，我们二分攻击次数判定是否成立。我们贪心的去想肯定要让攻击怪物溢出的尽可能少，因为溢出就浪费掉了。我们可以直接算出来每个攻击可以对应多少次。
我们发现 \(a_i\) 只能取 \(0,1,2\)，我们先考虑只能取 \(1,2\) 的情况，此时很显然我们只需要暴力填即可。如果加入 \(3\) 呢？我们需要尽可能避免浪费，往比 \(3\) 大的奇数和比 \(6\) 大的偶数里头放 \(3\)，把血量全都转化为 \(\{1,2,4\}\)，如果有剩余的 \(3\) 就往最大的里头填就行了。此时就转化为了攻击力只取 \(1,2\) 的情况。
- T700721 11.23 T1 - 深搜(dfs)
不是这场为什么人均 300+ 啊，我怎么只会 200。
我们先考虑没有子树 \(size\) 为奇数的情况，遍历后下一个的奇偶性没有产生变化。可以不管顺序遍历。如果子数 \(size\) 为奇数，那么此时遍历后下一个的奇偶性会取反。
然后就很板了，我们先让子树大小偶数的取其最大值，然后对子树大小为奇数的分成一半一半取即可。
- P14139 「SFMOI Round II」Strange Counting Game
观察到样例前五项全都是 \((n^2+1) \bmod (10^9+7)\)，猜测答案肯定是 \(n^2+k\) 的形式。我们把后面不为 \(n^2+1\) 的 \(n\) 扔到终端里头 factor 一下发现每一个都存在多个相同的质因数，无脑猜测一下 \(k\) 肯定和这个有关，猜到是所有出现了不只一次的质因数之积，但是这个显然很不对，因为可能会出现一些出现了不只两次的质因数。我们考虑怎么办。
打个表吧，然后注意到存在 \(k\) 个相同质因数的情况下其实是取了 \(\lfloor\frac{k}{2}\rfloor\) 的。这样做就行。
- P14146 朝花
怎么没人写树的做法，来一个。
我们考虑先把这个神秘的图变成一个森林的形式，我们只需要把环都消掉就行了，很显然的，我们付出的代价是 \(9m-9n+9\)。
对于一个仅有一个儿子节点的我们可以这样维护。
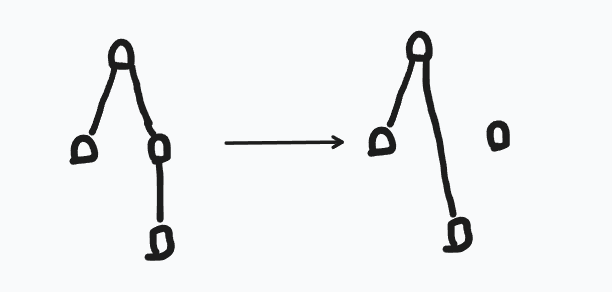
这样做的消耗是 \(9n\)。
对于一个有多个叶子节点的我们可以进行两步转化。
这样的消耗是 \(9+16=25\)，消掉了三个点，所以实则代价是 \(\frac{25}{3}n\) 的。
如果有超过两个甚至很多很多个呢？
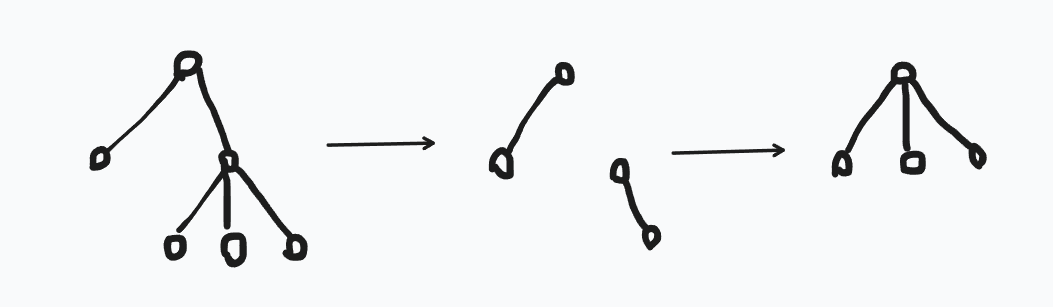
我们在这种时候这样连接的代价是 \(25+9\)，消掉了两个点，所以代价是 \(17n\) 的。
如果有四个以上我们就直接重复之前的，可以直接做。消到最后只剩下一条边，用样例二的做法是 \(88\) 代价的。
所以我们的总代价是 \(17n+9m+97\) 的，能做。
11.25
- P14411 [JOISC 2015] 道路建设 / Road Development
树剖题单出现动态加边？事已至此，LCT 启动！板子题。
我草这题题面好恶心。依旧经典的边权转点权，然后直接做即可。
- P14080 [GESP202509 八级] 最小生成树
我草怎么是最小生成树，有心理阴影了。考虑使用 LCT 维护，
首先很明显的是 LCT 当辅助树。对于加边的时候我们考虑两个可能：这条边还没有在最小生成树里头连通或者已经连通。对于前者我们可以直接选中这条边，对于后者我们找到用新边去找到原来在这个路径上的边权最大值，然后替换掉即可。
但是这道题不行。
浙公网安备 33010602011771号