【十一月上旬训练纪要】“她说 威诺希啊 威诺希 是你的失败,她说 威诺希啊 威诺希 别不知悔改。”
11.1
CSP 野鸡比赛能不能滚出 OI 啊
CSP 野鸡比赛能不能滚出 OI 啊
CSP 野鸡比赛能不能滚出 OI 啊
考的很烂,出来的时候正在下雨,原来我已经是高二老登了吗,可是——
11.2
考 CSP 烂完了,找 PrincessQi 玩,交流了一下,pcq 和我说我可以先板刷月赛绿题,ABC 或者 CF *1500,因为 TJ 是神秘弱省,NOIP 其实只需要 200+ 就比较稳了,至于模拟赛比较烂完了所以不要打(?)
不过模拟赛出现了 LCT 板子我感觉确实不是啥正常模拟赛
11.3
感觉没有发生任何比较有趣的事情?话说怎么都在打 FPS24,这是啥。
原题 AT_joisc2018_f。
题面比较邪恶,但是我们可以发现第 \(i\) 个人一定是在某回合后一下子走好多步,也就是 \(f_i\) 个回合后一下子移动 \(f_i\) 步。
我们考虑对于 \(f_i\),它与 \(f_{i-1}\) 的关系是:
-
若 \(f_{i-1}≥d_i\),那么在移动后 \(i\) 就直接移动了 \(f_i\) 步直接移动到了第 \(i-1\) 人的身后,保持同步,\(f_i = f_{i-1}\)
-
若 \(f_{i-1}<d_i\),那么在移动很多次之后才会移动,比较邪恶,这个时候 \(f_i=\lceil\frac{d_i}{f_{i-1}}\rceil f_{i-1}\)。
我们维护连续段,然后在询问时查询即可。
容易发现这个是一个冒泡排序,我们设 \(f_i\) 表示对于 \(a_i\),其前面的比它大的数的个数,在每一轮的排序中必然会导致 \(f_i - 1\),因为会有一个比他大的数在这个过程中与他交换,由于排序完成的条件是 \(\max\{p_i\}=0\),所以我们可以得出我们需要找的是 \(\max\{p_i\}≤k\) 的排列个数。
我们从小到大排序,可以发现 \(1\) 必须填到 \([1,k+1]\) 的位置,\(2\) 必须填到 \([1,k+2]\) 的位置……可以发现每个数都有 \(k+1\) 种填写方案,但是最后的 \(k\) 个数可以填的位置不够,只有 \(k!\) 种,那么我们可以算出方案数是 \(k!(k+1)^{n-k}\)。
对于 \(k>n\) 的情况我们特判,答案为 \(n!\)。
由于我写的时候很唐用数组存的阶乘,但是这道题是 \(n<10^{18}\),写个函数求就好了。
我去这道题我完全没思路啊,就只能看出来是二分答案,我怎么这么菜,但是我找题解能力比较强,找到了别人的题解,研究了一下。
我们可以很显然发现这道题是二分答案,我们二分时间 \(T\),计算对于 \(T\) 需要的总人数作为判断是否合法。
我们从右往左,去把工人分配给第 \(A_i\) 个设施,每个工人最多能检查的次数是 \(T-A_i\),而需要检查的次数是 \(\sum_{j=i}^{n}{B_j}-cnt\),这里的 \(cnt\) 是其他工人剩下的空闲检查次数,比较好发现对于这个 \(A_i\) 需要的工人数是 \(\lceil\frac{\sum_{j=i}^{n}B_j-cnt}{T-A_i}\rceil\) 人,我们维护一下总人数和 \(cnt\) 即可。
题目比较诡异,翻译一下其实是可以在整数时刻移动,只要在上个整数时刻到这个地方下个整数时刻直接跑路也算你过了一次活动。
感觉比较像是一个 dp,我们设 \(f_{0/1,w}\) 代表在 \(1/2\) 个城市,恰好参加了 \(w\) 个活动的最早结束时间。
对于一个 \(f_{i,w}\),其转移的路径有两条:跨城和同城,同城即 \(f_{i,w-1}≤S\),跨城即 \(f_{!i,w-1}+D+Kj≤S\)。
线段数优化即可。
哈哈你怎么知道我赛时想出来了做法死活想不起来怎么打最小生成树。
最显然的思路,直接跑一个最小生成树然后拿出 \(n-1\) 条边,暴力枚举 \(k\) 个二进制位然后建边跑最小生成树,复杂度 \(O(2^kkn \log n)\),不是很能过,发现这个 \(\log\) 太邪恶,考虑怎么去掉,这个瓶颈在于每次的排序。
直接在最开始就排序,然后跑的时候判断在不在考虑范围就行,复杂度 \(O(2^kkn)\) 过了。
11.4
JOI 能不能来点人类题面啊。
题意大概是给定 \(Q\) 个长度为 \(N\) 的只含有 abc 的字符串,可以翻转区间 \([1,k]\),问需要最少多少次变成字典序单调不降。
注意到 \(n<13\),而且只有 abc 三个字符,考虑直接把 abc 压成 \(012\),然后有一个很神秘的思路,因为所有询问的 \(n\) 都是一样的,考虑把 \(3^n\) 的状态全部用 BFS 预处理出来,从每一种状态搜索变成单调不降是不好做的,所以倒着做即可。
感觉比较深刻,最开始没什么思路,看了题解比较恍然大悟。
我们考虑对于一棵树,我们向下搜索时每次加深都在对应的字符串中加入 (,回溯时则加入 ),那么我们就会得到一个长度为 \(2n-2\) 的字符串,这个字符串对于一棵树构成双射,
很显然的就是深度是对于每个 ) 前面的 ( 的个数减去前面 ) 的个数,容易发现这个其实相当于是在 \(2n-2\) 的长度中搞出来 \(n-1\) 个 (),然后我们就能搞出来一个式子 \(ans=\binom{n-2}{2}\binom{n-4}{2}\cdots\binom{2}{2}\frac{1}{(n-1)!}\)。
感觉题目比较神秘,仔细想了一下发现这题是似乎最短路板子题,考虑如果一个点灯人如果在一个点在 \(x\) 可以待着那么必然可以在 \(x+2\) 时刻待着,我们考虑跑最短路求最小值,诶诶这个好像是奇偶最短路啊,没事我写的时候不知道,我不会奇偶最短路/dk。
我们发现我们每次进行这样来回绕圈跑此时 \(x\) 的奇偶性没变,我们可以分两层跑最短路,然后就解决了,记得特判所有人卡在 1 号城市出不去的时候。
这不是搜索板子题吗,懒得写了。
容易发现由于只能在两端删除,因此亮着的部分是一个连续段,我们设连续段为 \([l,r]\),然后先计算 \([1,l-1]\) 和 \([r+1,n]\) 的贡献,我们可以枚举两端 \(l,r\) 写一个转移方程得到一个 \(O(n^2)\) 的做法,但是比较邪恶的是这个做法好像过不了。
不过其实能发现跑一个三维前缀和+一个后缀和即可通过。
11.5
一早上就开始难受,没啥写题的欲望
我错了我再也不诋毁最小生成树了。
有一些比较暴力的想法比如把所有点都连起来然后硬做,一看复杂度 \(O(n^2 \log n^2)\) 过不去啊。
考虑先对边权排序,然后进行判断:
-
如果两边颜色相同并且颜色内部没有联通,那么我们设这个颜色有 \(x\) 个点,我们用 \((x-1)b\) 的代价把内部的点全部连起来即可,此时我们就可以把这一整个颜色缩为一个点。
-
如果两边颜色不同且没有联通,让两个点内部为 \(x,y\) 的话可以直接用 \(x+y-1\) 条边给连起来,算一下代价就行,然后把两个颜色缩点。
连通性可以并查集维护。
这题有绿?这题有绿?这题有绿?那我感觉绿题良莠不齐啊。
考虑每次移动的除了一次项以外还有一个常数,这个常数比较邪恶,所以考虑一次性尽可能多的运,限制我们的只有钱和时间,然后根据这两个进行调整即可。
神秘贪心题,思考一个接送的策略。
容易发现顺水是对答案没有影响的,只考虑对于逆行的情况。
对于一个 \(A\) 和 \(B\) 两个乘客(\(B<A\)),我们根据其中一个的目的地和另一个的出发点来考虑策略,容易发现:
-
如果 \(A\) 的目的地在 \(B\) 的出发点之前,那么我们可以拿到 \(A\) 再退回 \(B\) 之前把那个人送过去就行。
-
如果 \(A\) 的目的地在 \(B\) 的出发点之后,那么就先送 \(A\) 再跑 \(B\) 的即可。
这个应该是比较显然的吧,你就考虑怎么才能不多跑原本不需要多跑的部分。
好久没看到 SPJ 了话说,看看怎么做。
这题感觉不算很恶心,你先把时间转化为秒数,这个时候每个时间都对应了一个独一无二的秒数(显然),然后跑一个区间加的线段树,线段树维护区间 \(+1\) 和区间和即可。
11.6
我们把整个区间分为三个部分:\([1,l-1]\),\([l,r]\),\([r,n]\)。最朴素的方法:对于每个 \(l\) 枚举 \(r\)。复杂度是平方级别的过不去,考虑优化。
我们发现对于一个区间 \([l,r]\),我们扩展一位变为 \([l-1,r]\) 或者 \([l,r+1]\),新得到的 \(\gcd\) 是原本区间 \(\gcd\) 的因数,容易发现最多降低 \(\log\) 次。
我们固定住一个端点,此时影响的就只有左端点 \(\gcd\) 的前缀和,发现左端点保持不变的情况下中间一段边长不会使答案变大,所以只取每段前缀 \(\gcd\) 相等区间的右端点作为前缀 \(\gcd\) 的计算即可。
傻子模拟题,不写但是给你挂题单里。
注意到下降不消耗电量,我们考虑对于初始起点 \(f\) 对所有人分为两类:\(r_i<f\) 和 \(r_i>f\) 的。我们必然优先处理 \(r_i>f\) 的人,因为下降不消耗电量,不然会比较麻烦。我们对于 \(r_i>f\) 内部按照 \(l_i\) 排序,优先处理比较小的即可。
哈哈我不会字符串,赛时获得 0pts 的优秀成绩。
有一个比较显然的就是如果 \(|t_1|\not=|t_2|\),那么答案必然为 0,因为 \(|s_1|=|s_2|\) 无论怎么变换都变换不过去,不过我当时没看到,真是一对苦命鸳鸯/dk。upd:并非苦命,没卡这个。
后面的以后再补,写别的题去了,蹲一下 wang5 博客。
upd:wang5 居然更新了,但是我不想补,后面再说。
11.7
这题好像是签到题,容易发现移动唯一的影响只有把 \(S[1]\) 转移到 \(S[n]\) 处的时候会减少一次,把一个偶数串变成两个奇数串喵,然后暴力计算即可喵。
这题好像也是签到题,容易发现需要优先让各个队伍变成 \(k\) 的整数倍,我们按照距离 \(k\) 的整数倍的差进行排序,如果能全部填满剩下的直接计算就行了。
打个表先 \(\{1,0,2,4,3,5,6,8,7,9,10,12,11\}\),可以很简单的发现对于这种 impossible 的情况只出现在 \(n \pmod 4 = 0\) 的地方以及 \(n=1\) 两种情况下。
11.10
周末玩了两天,困死了呜呜呜。
来写 shadow 大人的题单喵。
我们对于每个房子做差分,这是显然的。变成 \(n-1\) 个点,第 \(i\) 个点代表大楼 \(i\) 与 \(i+1\) 的距离之差。
原题转化为不能选取相邻的两个点,最小化总和。我们建立一个优先队列维护,每次取出最小的点,然后把周围两个点不让取,但是这样不对,因为我们这样会放弃一些比较小的可能。
我们可以把抛弃掉的点转化为 \(a_{i-1}+a_{i+1}-a_{i}\),当我们选取这个点的时候前面必然也选取到了 \(a_i\),此时就变成了不选 \(a_i\) 而是选 \(a_{i-1}\) 和 \(a_{i+1}\)。
上道题的双倍经验,应该是。
11.11
懒得写了,直接放图
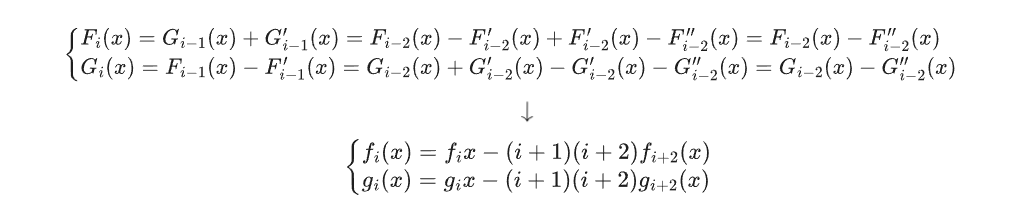
然后你把下面这个拆开变成组合数的形式就行了,我懒得写题解了。
最开始想了一个贪心做法,不是很优,现在写个 dp 试试。
我们设一个 \(f_i\) 表示到达位置 \(i\) 时的答案,那么我们就很容易做,从 \(f_{0,1,\cdots,i-1}\) 转移到 \(f_i\) 的转移方程是:\(f_i = \min_{j=0}^{i-1}\max(f_{j}+t_2j,ik)+t_2\times j+t_1\times(i-j)\)。
复杂度 \(O(m^2)\),如果是考试我估计我就直接跑路了,可以得到 90 分,考虑优化一下。
容易发现 \(f_j+t_2j\) 是单调递增的,我们可以直接把 \(\min\) 拆掉。然后直接维护,复杂度 \(O(m)\) 线性。
这题有紫?首先考虑构造贪心策略。容易发现我们肯定会尽可能让所有的泡面都进入一个碗里,容易想到要归到区间内泡面数最多的桶里。
我们设余下区间的最大值为 \(a\),总和为 \(sum\),很容易想到对于对于 \(a\le\frac{sum}{2}\) 的情况下需要的次数为 \(\frac{sum}{2}\) 次:我们每次选取剩下的最大,次大的元素对我们最开始选出的泡面桶中放泡面。
但是有的时候 \(a\) 太大了啊,比一半的 \(sum\) 都大,这样贪心肯定没得做,怎么办呢?我们可以考虑先对 \(a\) 进行操作给其他的不是我们最开始要全都放进去的桶,每一次都会让 \(a\) 减去 1 而 \(sum\) 不变,这样就可以变成 \(a = \frac{sum}{2}\) 的情况。此时我们可以发现操作次数为 \(a\) 次,这个也是显然的。
但是我们发现在 \(2\nmid sum\) 的情况下这个是不成立的。我们在最开始要归位到的桶里头拆一个就行,这个时候 \(sum+1\) 自然而然就变成偶数了,可以直接按照偶数的方法去做。
我们容易发现前面的想法必然需要 \(len\ge3\),那么 \(1,2\) 的情况怎么做呢?特判即可。
对于 \(len=1\) 的情况我们发现开局这个桶就填满了,完全不需要操作,\(0\) 次。
对于 \(len=2\) 的情况我们只需要从两个位置拆一下就变成 \(len=3\) 了,可以直接做,不过我们发现如果一个数是 \(1\) 另一个是 \(2\) 的时候是完全做不了的,只要动一下就会自动回退成一个 \(1\) 一个 \(2\) 了,此时无解。
很显然我们需要维护的是区间最大值,区间次大值,区间和,随便挂个 ds 就行。
等一下一些比较人话的题解,我不觉得在已经给出序列为 \(1-n\) 的排列的情况下还需要设值域为 \([1,m]\),所以我认定题解不像是人类,这题后面再说吧。
11.12
11.18
我中间这几天干啥了怎么没写这个
主播主播你怎么没写过春测的题,我错了不要再拷打我了我这就补题。
当 \(k>2\) 的时候可以直接暴力去做,这个很显然。当 \(k=2\) 的时候我们思考发现完全平方数有 \(\sqrt n\) 个,去掉被标记过的即可。
考虑这个 \(f(n)\) 其实是 \(n-\varphi(n)\),对于部分分我们有一个很优的做法:直接线性筛欧拉函数暴力计算差值。可以获得:40pts。
但是暴力线性筛的话显然是对数据范围达到 \(1e18\) 的本题是无法获得全部分数的。我们发现在最下面给了一个 PR,肯定是要单点求的啦!
注意到 \(\varphi(pq)=(p-1)(q-1)\),因此 \(f(pq)=p+q-1\),因为这个值是 \(m\),所以 \(p+q=m+1\)。
容易得出。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号