动态规划Part1
动态规划\(Part1\)
个人理解:dp相对于爆搜所能优化的原因在于dp存在转移时的决策,比如01背包每次都会从前i-1个物品中的最优决策中转移过来,这样省去考虑了哪些不优的方案
状态压缩dp
X>>1;//二进制数向右移一位
x<<1;//左移,左边x是要进行变化的数,1是指向左移1位
//左移右移都用0补齐,因此左移右移都有可能改变符号
//0^1=1 1^1=0 异或1是取反操作
//1^0=1 0^0=0 异或0是保留操作
//1&1=1 0&1=0 0&0=0 1&0=0 &1是保留操作,&0是变成0
//1|1=1 0|1=0 1|0=1 0|0=0 对1取或,得1,对0取或,保留原样
x^1;//对最后一位取反
x^0;//保留x
x|(1<<(k-1));//使右数第k位为1
x&(~(1<<(k-1)));//使第k位为0,将只有第k位为1的数取反,然后&
x^(1<<(k-1));//第k位取反
x&(-x);//-x是x取反后+1,由于lowbit前面位置全相反,所以为0,然后 //lowbit及其之后一致,则可得到lowbit,右数最低位的1,10进制大小
x&((1<<k)-1);//取右数第k位到右数第一位
(x<<1)+1;//在x最后增一个1 如011->0111
x<<1;//最后增0
x|1//在把末尾变成1
x|1-1//把末尾变成0
x>>(k-1)&1//求第k位为0还是为1
x&(1<<(k-1));//若为0则第k位为0,反之非0,用于判定第k位
x|((1<<k)-1);//使右数第k位到右数第一位为1
x^((1<<k)-1);//使右数第k位到右数第一位取反
x&((~1<<(k-1))+1))//使右数连续的1变成0,自己想的,需要知道连续几个(k-1)个
x&(x+1)//使右数连续的1变成0
x|(x+1)//右数第一个0变成1
x|(x-1)//使末尾连续的0变为1
(x^(x+1))>>1//取出末尾连续的1
(x&(x-1)>>1)//取出末尾连续的0
单调队列优化
#include<bits/stdc++.h>
using namespace std;
int a[1000005],q[1000005],head=1,tail=1;
int main()
{
int n,k;
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
while(head<tail&&a[q[tail-1]]>=a[i])
tail--;
q[tail++]=i;
if(head<tail&&q[head]<i-k+1) head++;
if(i>=k) printf("%d ",a[q[head]]);
}
printf("\n");
return 0;
}
01背包
acw1022. 宠物小精灵之收服
状态表示:
f[i] [j] [k] :i个小精灵,皮卡丘体力值为m,精灵球数为z
属性:最大捕捉小精灵数量
转移方程:
O(NMK)算法
该题本质是01背包,一共i个精灵的选择是从i-1个精灵选择中转移过来的,需要加上最后一个精灵的选与不选的不同变化,每次选择能使当前所捕捉小精灵数量最多
不同点:
1.本题有体力值和精灵球数量两个限制
2.且需要在存储空间上优化掉精灵数量这一维度
3.细节,最终体力值不能为0
4.在同等的捕捉数量求体力值损耗最小
解决方法:1.加上一维即可
2.优化方法使用滚动数组变量从大往小滚动,每次转移使用的仍然是前i-1个精灵的情况下的数值
3.把每个体力损耗+1,或者除去体力值为0的情况
4.多加一个数组保存损耗值,捕捉数量一致的时候使用损耗小的那个
#include <bits/stdc++.h>
using namespace std;
int f[505][1005], w[1005], v[505], hs[505][1005];
int main()
{
int n, m, k;
// freopen("ipt.txt", "r", stdin);
// freopen("opt.txt", "w", stdout);
cin >> n >> m >> k;
for (int i = 1; i <= k; i++)
cin >> w[i] >> v[i];
// cout << "s" << endl;
for (int i = 1; i <= k; i++)
for (int j = m; j > v[i]; j--)
{
for (int z = n; z >= w[i]; z--)
{
if (f[j - v[i]][z - w[i]] + 1 > f[j][z])
{
f[j][z] = f[j - v[i]][z - w[i]] + 1;
hs[j][z] = hs[j - v[i]][z - w[i]] + v[i];
}
else if (f[j - v[i]][z - w[i]] + 1 < f[j][z])
{
f[j][z] = f[j][z];
hs[j][z] = hs[j][z];
}
else
{
f[j][z] = f[j][z];
if (hs[j][z] < hs[j - v[i]][z - w[i]] + v[i])
{
hs[j][z] = hs[j][z];
}
else
{
hs[j][z] = hs[j - v[i]][z - w[i]] + v[i];
}
}
// cout << f[j][z] << endl;
// cout << hs[j][z] << endl;
}
}
cout << f[m][n] << " " << m - hs[m][n] << endl;
return 0;
}
O(K^2M)
思路来源于acwing @墨染空
由于本题数据
N小智的精灵球数量、M皮卡丘初始的体力值、K野生小精灵的数量。
0<N≤1000
0<M≤500
0<K≤100
本题求使用精灵球数最小或耗费体力最小的集合都包含捕捉数量最大的情况
(原因代补)
而N最大,K最小,故k*k再乘m复杂度最小
因此举一反三,有时可以看数据进行优化
完全背包

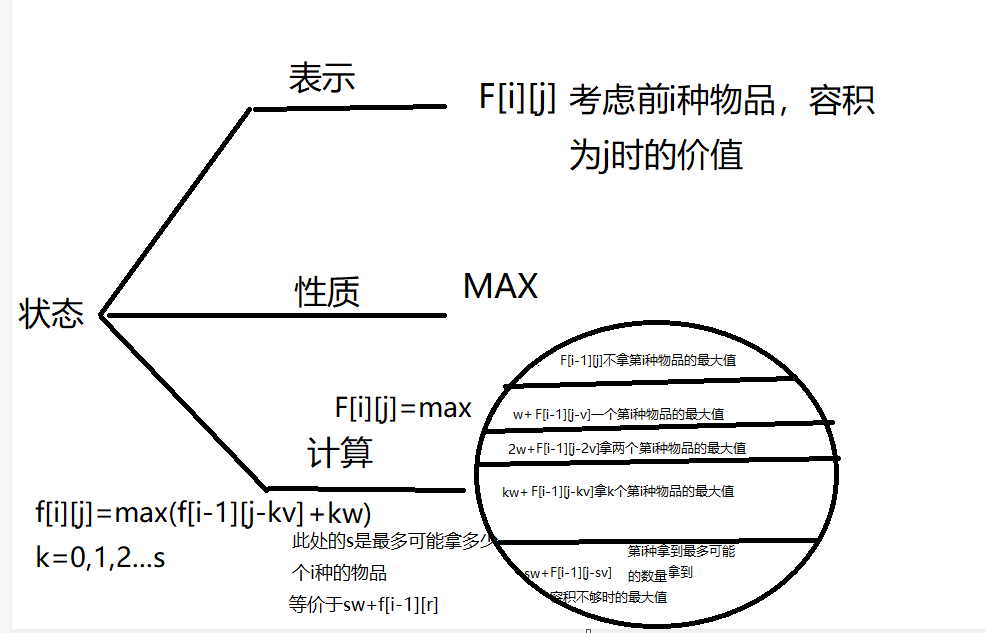
由状态转移\(f[i] [j]=max(f[i-1] [j-k*v]+kw) (k=0,1,2,3..s)\quad s=j/v\)得到
朴素版
时间复杂度\(O(NV^2)\)
空间复杂度\(O(NV)\)
for(int i=1;i<=N;i++)
for(int j=0;j<=V;j++)
{
for(int k=0;k*v[i]<=j;k++)
{
f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
\(F[i][j]=max(F[i-1][j],F[i-1][j-v]+w,...,F[i-1][j-kv]+kw,...,F[i-1][j-sv]+sw)\quad s=j/v[i]\)
\(F[i][j-v]=max(F[i-1][j-v],F[i-1][j-2v]+w,...,F[i-1][j-kv]+(k-1)w,...,F[i-1][j-sv]+(s-1)w)\quad s=j/v[i]\)
推得
\(F[i][j]=max(F[i-1][j],F[i][j-v]+w)\quad s=j/v[i]\)
时间复杂度优化版本
时间复杂度\(O(NV)\)
空间复杂度\(O(NV)\)
for(int i=1;i<=N;i++)
for(int j=0;j<=V;j++)
{
f[i][j]=f[i-1][j];
if(j-v[i]>=0)
f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);//因为j-v[i]需要不小于0,否则越界
}
进一步发现当j>=v[i]时都可能由F[i] [j-v]+w的分支转移过来,若从大到小遍历容积j则每次使用的状态是比当前j小的f[i] [j-v],则可以优化为一维数组且且转移过程不会覆盖掉需要的f[i] [j-v]状态,又能与之前存在f[j]中的f[i-1] [j]直接对比
最终优化版本
时间复杂度\(O(NV)\)
空间复杂度\(O(V)\)
for(int i=1;i<=N;i++)
for(int j=v[i];j<=V;j++)//j<v[i]的会直接继承f[i-1][j]的状态
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
多重背包
多重背包一面是数量更大的01背包,一面又是数量有限的完全背包
多重背包二进制优化法
将某种物品的数量s首先尽量拆分成一个二进制等比数列每个数是看做单独的物品,减去这个等比数列和,最后会剩余下不是刚好2^k数量作为单独一个物品,同时体积和价值翻倍到与数量同倍
理论基础
当x表示成一系列二进制数的和时,从这些二进制数中选取数可以组成0~x的所有数
例:数10可以表示为
\((1010)_B=(0111)_B+(0011)_B=7+3\)
在二进制优化时会拆分\(7=(0111)_B=(0001)_B+(0010)_B+(0100)_B\)
即\(10=(1010)_B=(0001)_B+(0010)_B+(0100)_B+(0011)_B\)
1.可以选择不同的数位相加组成0~7的数
2.用上面的0~7加上3可以表示
\((0111)_B+(0011)_B=7+3=10\)
\((0110)_B+(0011)_B=6+3=9\)
\((0101)_B+(0011)_B=5+3=8\)
表示了8~10的数
则可以表示0~10的数
所有正数都可以拆分成\(s=a+b\),\(a\)是0s中二进制数位从最低位到最高位都是1且最大的数,这样可以用它表示成0a的数,而a+1s的数都可以用0a的数加上b得到
证明:
即证a+b>=s且0+b<=a+1
1.a+b>=s:a+b=s,则a+b>=s成立
2.0+b<=a+1:反证法,假设b>a+1,则b本应该成为新的最高数位,这样a就不满足前提,则0+b<=a+1
#include <bits/stdc++.h>
using namespace std;
int w[1005], v[1005], s[1005], nw[20005], nv[20005], num = 0, f[2005];
int main()
{
int N, V;
scanf("%d%d", &N, &V);
for (int i = 1; i <= N; i++)
{
scanf("%d%d%d", &v[i], &w[i], &s[i]);
int t = s[i], countn = 1, sum = 0;
while (countn * 2 - 1 <= s[i])
{
nv[++num] = countn * v[i];
nw[num] = countn * w[i];
countn *= 2;
}
if( (s[i] - countn + 1))
{nv[++num] = (s[i] - countn + 1) * v[i];
nw[num] = (s[i] - countn + 1) * w[i];}
}
for (int i = 1; i <= num; i++)
{
// cout << i << " " << nv[i] << " " << nw[i] << endl;
for (int j = V; j >= nv[i]; j--)
{
f[j] = max(f[j - nv[i]] + nw[i], f[j]);
// if (f[j] == 100)
// cout << i << " " << j << endl;
// cout << f[j] << endl;
}
}
cout << f[V] << endl;
return 0;
}
优化代码
while(cnt<=t)
{
nv[++num]=v[i]*cnt;
nw[num]=w[i]*cnt;
t-=cnt;
cnt*=2;
}
if(t)
{
nv[++num]=v[i]*t;
nw[num]=w[i]*t;
}
多重背包单调队列优化
切入点:我们知道完全背包中的状态\(F[i][j]\)可以用\(F[i][j-v]+w[i]\)和\(F[i-1][j]\)
转移过来,即可以利用已经计算出的信息同为前i个物品中选择的但体积更小的状态\(F[i][j-v]\)来减少对比的运算次数:
\(F[i][j]=max(F[i-1][j],F[i-1][j-v]+w,...,F[i-1][j-kv]+kw,...,F[i-1][j-sv]+sw)\quad s=j/v[i]\)
\(F[i][j-v]=max(F[i-1][j-v],F[i-1][j-2v]+w,...,F[i-1][j-kv]+(k-1)w,...,F[i-1][j-sv]+(s-1)w)\quad s=j/v[i]\)
这里因为每个数同时加上一个数不会影响大小关系,所以可以
\(F[i][j]=max(F[i-1][j],F[i][j-v]+w)\quad s=j/v[i]\)
但是多重背包的不像完全背包那样所有类型的物品都能单独填满背包,它的数量是有限的,因此没法直接计算出每种类型最多多少物品,即\(F[i][j-v]\)可能不会完全等于\(F[i][j]\)的后半部分,比如假设第i个物品最多为s个,而背包最多放t(t>s)个,于是比较得到\(F[i][j-v]\)会比\(F[i][j]\)多比较\(F[i][j-(s+1)v]+sw\)
通过观察发现当j变化时最多可以放下i种物品的数量m也会发生变化,当体积\(j<s*v[i],m<s;j>=s*v[i],m=s\)
且发现当\(F[i][j]\)和\(F[i][j-v]\)虽然末尾和开头不一样,但是中间的部分都一致,且这种规律使用于除了边界条件以外的所有j,这是在一个固定大小的窗口中求最大值,则可以用单调队列优化(单调队列可以求从窗口大小0不断放入元素直到等于上限以及达到上限之后滑动的最大值,所以处理体积不到能放下所有该类物品时也可以)
\(k=j/v[i],r=j\%v[i]\),我们从\(F[i][r]\)开始求状态,
\(F[i][r]=max(F[i-1][r])\)
\(F[i][r+v]=max(F[i-1][r+v],F[i-1][r]+w)\)
\(F[i][r+2v]=max(F[i-1][r+2v],F[i-1][r+v]+w,F[i-1][r]+2w)\)
\(...\)
\(F[i][r+kv]=max(F[i-1][r+kv],F[i-1][r+(k-1)v]+w,...,F[i-1][r+v]+(k-1)w,F[i-1][r]+kw)\)
\(F[i][r+(k+1)v]=max(F[i-1][r+(k+1)v],F[i-1][r+kv]+w,...,F[i-1][r+2v]+(k-1)w,F[i-1][r+v]+kw)\)
\(...\)
\(F[i][j-v]=max(F[i-1][j-v],F[i-1][j-2v]+w,...,F[i-1][j-kv]+(k-1)w,...,F[i-1][j-(s+1)v]+sw)\quad s=j/v[i]\)
\(F[i][j]=max(F[i-1][j],F[i-1][j-v]+w,...,F[i-1][j-kv]+kw,...,F[i-1][j-sv]+sw)\quad s=j/v[i]\)
在状态转移的过程中不同的j和i导致r不同,对于背包容积j,前i种物品决策第i种选几个时,\(j\%v[i]\)相等的j的状态\(F[i][j]\)都位于由余数\(r\)分割的数列\(F[i][r+kv],k=0,1,...\)上,每次将将\(F[i-1][j]\)放入单调队列中,并与单调队列中的元素比较(需要加上对应的w[i])得到\(F[i][j]\)
则在动态规划时可以将 for (int j = V; j >=0; j--)
变成for (int j = 0; j < v[i]; j++)
即按照余数划分体积,并且通过循环每次体积\(+v[i]\)得到所有余数为该数的体积j前i种物品中选择的最大值\(F[i][r+kv]\) \((F[i][j])\)
#include <bits/stdc++.h>
#define MAXN 20005
using namespace std;
int w[1005], v[1005], s[1005], f[20005];
//id是目前是同余数r数列(下成为r数列)中第几个,通过id与单调队列中的元素在r数列中的下标相差与w积求实际的队列元素大小
long long dddl(int &head, int &tail, int x, int id, int b[], int q[], int k, int w)
{
while (head < tail && b[tail - 1] + (id - q[tail - 1]) * w < x)
{
tail--;
}
b[tail] = x;
q[tail++] = id;
while (head < tail && q[head] < id - k)//单调队列中实际是放k+1个数,则队列中数列下标最小的不能小于
head++;
return b[head] + (id - q[head]) * w;
}
int main()
{
int N, V;
scanf("%d%d", &N, &V);
for (int i = 1; i <= N; i++)
{
scanf("%d%d%d", &v[i], &w[i], &s[i]);
}
for (int i = 1; i <= N; i++)
{
for (int j = 0; j < v[i]; j++)
{
int head = 1, tail = 1, b[MAXN], q[MAXN]//b是单调队列里的价值(不加w),q表示同余数r数列中第几个;
for (int k = 0; j + k * v[i] <= V; k++)
{
long long t = dddl(head, tail, f[j + k * v[i]], k + 1, b, q, s[i], w[i]);
f[j + k * v[i]] = t;
}
}
}
cout << f[V] << endl;
return 0;
}
本文来自博客园,作者:多巴胺不耐受仿生人,转载请注明原文链接:https://www.cnblogs.com/VoidCoderTF/articles/15944627.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号