贪心模型

最少点覆盖问题等价于最大不相交集合数问题

在二分图匹配，以及贪心算法里面可以体现

原因：最少点覆盖，每组两两有交集的区间构成一个等价类集合，点数就是集合数，集合之间的区间不相交，集合内部区间相交

最大不相交的数量==最少覆盖的点数

最少覆盖的点数是上述定义的不相交的集合数量

因为若最大不相交的数量 <最少覆盖的点数,则存在等价类之间区间相交的，矛盾

若最大不相交的数量 >最少覆盖的点数 则存在集合内部存在不相交，矛盾

#include<bits/stdc++.h>
#define INF (int)(1e9+5)
using namespace std;
struct S
{
int l,r;
}s[100005];
bool cmp(S a,S b)
{return a.l<b.l;}
int main()
{
    int n,countn=0;
    cin>>n;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d%d", &s[i].l,&s[i].r);
    }
    
    sort(s+1,s+1+n,cmp);//左端点小到大排列
    s[0].r=-INF;
    int t=-INF;
    for (int i = 1; i <= n; i ++ )
    {
        
        if(s[i].l>t)//若左端点大于当前交集的右端点，则点增加
        {
            countn++;
            // cout << s[i].l<<" "<<s[i-1].r<<endl;
                 t=s[i].r;
            
        }
        else t=min(s[i].r,t);//更新交集右端点
   
        
    }
    cout << countn<<endl;
    return 0;
}

区间分组

方法1：求最大冲突组数

设要最小被分为k组

若最大冲突数为n，则最多时有n个区间有交集，则最小组数k=n组，因为少于有重叠，非可行解；

可以通过给起点终点离散化后，加入特定的标志，使其能够辨别是终点还是起点，得遍历每次遇到起点cnt++，遇到终点cnt--，求cnt过程的最大值

方法2：贪心

区间左端点从小到大排列，若当前区间左端点与当前最小右端大，则删除堆顶，然后将当前区间右端点加入堆，否则组增加(待证明)

#include <bits/stdc++.h>
using namespace std;
struct edge
{
    int l, r;
} a[100005];
bool cmp2(edge a, edge b)
{
    return a.l < b.l;
}
int main()
{
    int n, ans = 1;
    cin >> n;
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &a[i].l, &a[i].r);
    sort(a + 1, a + 1 + n, cmp2);

    priority_queue<int, vector<int>, greater<int>> qp;

    for (int i = 1; i <= n; i++)
    {
        if (qp.empty() || a[i].l > qp.top())
        {

            if (!qp.empty())
            {
                qp.pop();
            }

            qp.push(a[i].r);
        }
        else
        {
            ans++;
            qp.push(a[i].r);
        }
    }
    cout << ans << endl;
    return 0;
}

区间覆盖

性质：该问题符合最优子结构（反证法可证）:区间覆盖最小区间数可由区间右端点左移的覆盖最小区间数推出

思路：

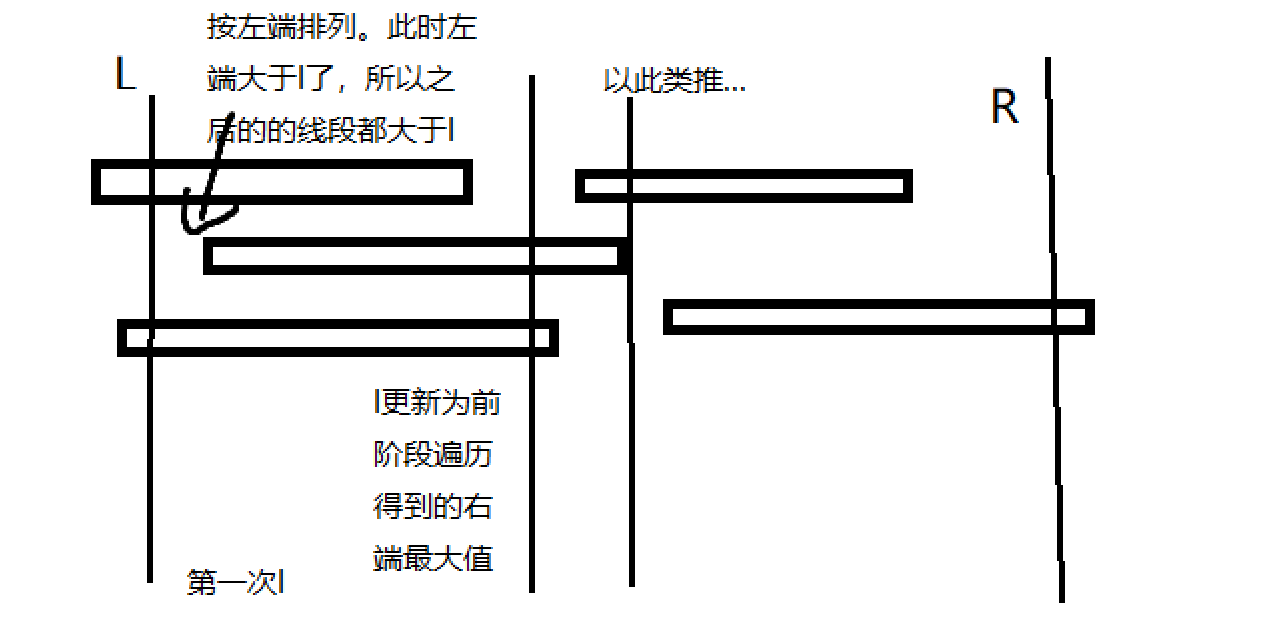
左端点从小到大排列，判断最小的是否小于等于当前左边界，若否则无解，若有则求满足该条件区间集合右端点最大值（左边界以左的可以消去，结果是满足条件的区间左边界以右部分的比较），直到左端点大于该边界，此时是覆盖从此时将左边界赋值为前集合右端点最大值，得到覆盖从左边界到此右端点的最优解，转换为判断新区间覆盖的最小区间数。

#include <bits/stdc++.h>
using namespace std;
struct s
{
    int l, r;
} a[100005];
bool cmp(s a, s b)
{
    return a.l < b.l;
}
int main()
{
    int s, t, n, ans = 0;
    cin >> s >> t;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d%d", &a[i].l, &a[i].r);
    }
    sort(a + 1, a + 1 + n, cmp);

    int l = s, r = -INT_MAX, i = 1, last = 1;
    while (r < t && i <= n&&l >= a[i].l)
    {
        while (l >= a[i].l && i <= n)
        {
            r = max(r, a[i].r);
            i++;
        }
        l = r;
        ans++;
    }
    if (r >= t)
        cout << ans << endl;
    else
        cout << -1 << endl;
    return 0;
}