GPLT_L2选集P1

L2-004 这是二叉搜索树吗？（dfs/并查集)

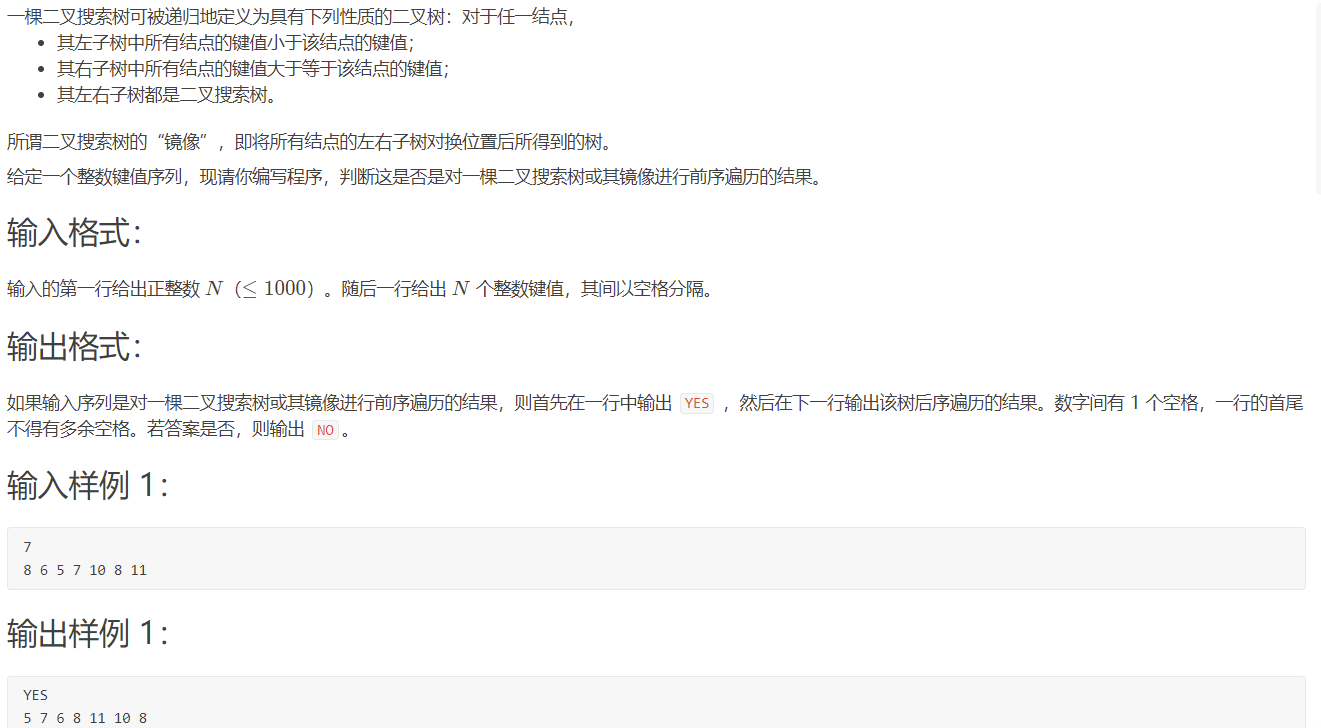
解法1：前序和中序求后续

方法：从中序遍历中找前序的首字符，得到求树根分割中序遍历字符串，继续分割得左右子树然后递归查找（使用双指针分割两个序列[l，r]）

原理：按照题意，右子树都是等于大于根节点的节点，若中序遍历是从小到大的，则查找第一个相等字符作为根节点，该节点左侧都是左子树，右侧是右子树，递归查找。

同理若中序遍历是从大到小，则查找最后一个相等的数，左侧是右子树，右侧左子树。

边界：当中序指针l>r时,即分割得到某子树是空树时，返回1，因为此时该子树遍历完毕，否则要一直递归。l<=r时都可以正常查找

判定是否是二叉树：若在中序查不到前序首字符则返回0

#include <bits/stdc++.h>
using namespace std;
// struct tree
// {
//     int l, r, data;
// } t[1005];
int pre1[1005], in1[1005], in2[1005], last[1005], cnt;
int judge(int pre[], int &prel, int prer, int in[], int inl, int inr)
{
    if (inl > inr)
    {
        return 1;
    }

    int x = -1;
    for (int i = inl; i <= inr; i++)
    {
        if (in[i] == pre[prel])
        {
            x = i;
            prel++;

            break;
        }
    }
    if (x == -1)
        return 0;
    else
    {
        int a = judge(pre, prel, prer, in, inl, x - 1);
        int b = judge(pre, prel, prer, in, x + 1, inr);
        last[++cnt] = in[x];
        return a && b;
    }
}
int judge2(int pre[], int &prel, int prer, int in[], int inl, int inr)
{
    if (inl > inr)
    {
        return 1;
    }

    int x = -1;
    for (int i = inl; i <= inr; i++)
    {
        if (in[i] == pre[prel])
        {
            x = i;
        }
    }
    if (x == -1)
        return 0;
    else
    {
        prel++;
        int a = judge(pre, prel, prer, in, inl, x - 1);
        int b = judge(pre, prel, prer, in, x + 1, inr);
        last[++cnt] = in[x];
        return a && b;
    }
}
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> pre1[i];
        in1[i] = pre1[i];
    }
    sort(in1 + 1, in1 + n + 1);
    for (int i = 1; i <= n; i++)
    {
        in2[i] = in1[n - i + 1];
    }
    int l = 1;
    if (judge(pre1, l, n, in1, 1, n))
    {
        cout << "YES" << endl;
        for (int i = 1; i <= cnt; i++)
        {
            cout << last[i];
            if(i!=cnt)
                cout<< " ";
        
        }
    }
    else
    {
        cnt = 0;
        l = 1;
        if (judge2(pre1, l, n, in2, 1, n))
        {
            cout << "YES" << endl;
            for (int i = 1; i <= cnt; i++)
                       {
            cout << last[i];
            if(i!=cnt)
                cout<< " ";
        
        }
        }
        else
            cout << "NO" << endl;
    }
    return 0;
}

解法2:构造二叉排序树

结论：按照二叉排序树的前序遍历顺序插入构造二叉排序树时，得到的树前序遍历与插入时的顺序一致，且逆命题成立，则可以通过检查构造后的前序遍历是否与插入时一致判断是否是二叉排序树的前序遍历

若前序遍历是镜像树的，其插入结果为原二叉排序树，此时查前序遍历要反过来遍历

L2-005 集合相似度 (25 分)(STL/复杂度优化)

题目思路

在输入集合元素时构造集合并求出该集合与已经出现的集合的交并集，之后在查询语句中调用

使用STL简化\(∩\)和\(∪\)操作

set_intersection(A.begin(),A.end(),B.begin(),B.end(),inserter(C,C.begin()));

set_union(A.begin(), A.end(), B.begin(), B.end(), inserter(D, D.begin()));

时间复杂度优化过程

1.\(O(KM)≈1.2e^8\)

每条查询语句插入元素STL构造集合

TLE

2.\(O(KM)≈0.8e^8\)

在输入每个集合元素时使用STL构造集合，查询语句中构造交并集

TLE

3.\(O(N^2M)≈0.5e^8\)

事先在插入构造集合时，求所有集合的交或并集，之后在k条查询语句时可以以O(1)的复杂度直接输出

AC

之所以3能够AC但2不能是因为2会有反复构造的交并集，这是已经计算出的信息，可以被存储

#include <bits/stdc++.h>
using namespace std;
set<int> a[55];
double ans[55][55];
int main()
{
    int n, k;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        int m;
        scanf("%d", &m);

        for (int j = 1; j <= m; j++)
        {
            int t;
            scanf("%d", &t);
            a[i].insert(t);
        }
        for (int j = 1; j <= i; j++)
        {
            int inter, uni;
            set<int> C, D;
            set_intersection(a[i].begin(), a[i].end(), a[j].begin(), a[j].end(), inserter(C, C.begin()));
            set_union(a[i].begin(), a[i].end(), a[j].begin(), a[j].end(), inserter(D, D.begin()));
            inter = C.size();
            uni = D.size();
            ans[j][i] = ans[i][j] = inter * 1.0 / uni * 100;
        }
    }
    scanf("%d", &k);
    while (k--)
    {
        int a1, b1;
        scanf("%d%d", &a1, &b1);

        printf("%.2lf%\n", ans[a1][b1]);
    }

    return 0;
}

L2-007 家庭房产 (25 分)(DFS)

题目思路

定义结构体：人与家庭，人包括父母孩子和房产套数和房产面积，家庭为总房产套数和房产面积以及最小编号

注意在在读入语句时同时更新其父母的孩子和孩子的父母的信息

记录读入过的编号，遍历0~9999，对未访问过的连通块进行访问并设置为家庭并更新家庭数量

每访问一个人则更新其家庭的信息，结构体排序输出

本题原本是并查集，但是我用dfs也做出来了（调了很久）

读题错误：没有读出编号有为0000的情况

#include <bits/stdc++.h>
using namespace std;
struct p
{
    int a[15], k, f, m;
    long long num, area;
} pp[10005];
struct fam
{
    long long num, area;
    int peo, minn;
} fam[10005];
int h[10005], vis[10005];
int n, cnt = 0;
bool cmp(struct fam a, struct fam b)
{
    if (a.area * 1.0 / a.peo > b.area * 1.0 / b.peo)
        return 1;
    else if (a.area * 1.0 / a.peo == b.area * 1.0 / b.peo)
    {
        return a.minn < b.minn;
    }
    else
        return 0;
}
void dfs(int now)
{
    vis[now] = 1;
    fam[cnt].minn = min(fam[cnt].minn, now);
    fam[cnt].num += pp[now].num;
    fam[cnt].area += pp[now].area;
    fam[cnt].peo++;
    if (pp[now].f != -1)
    {
        if (!vis[pp[now].f])
            dfs(pp[now].f);
    }
    if (pp[now].m != -1)
    {
        if (!vis[pp[now].m])
            dfs(pp[now].m);
    }
    for (int i = 1; i <= pp[now].k; i++)
    {
        if (!vis[pp[now].a[i]])
            dfs(pp[now].a[i]);
    }
}
int main()
{
    for (int i = 0; i <= 9999; i++)
    {
        pp[i].f = pp[i].m = -1;
    }
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        int t, f, m, k;
        scanf("%d%d%d", &t, &f, &m);
        scanf("%d", &pp[t].k);
        h[t] = 1;
        pp[t].f = f;
        pp[t].m = m;

        if (f != -1)
        {
            h[f] = 1;
            pp[f].k++;
            pp[f].a[pp[f].k] = t;
        }

        if (m != -1)
        {
            h[m] = 1;
            pp[m].k++;
            pp[m].a[pp[m].k] = t;
        }

        for (int j = 1; j <= pp[t].k; j++)
        {
            scanf("%d", &pp[t].a[j]);
            h[pp[t].a[j]] = 1;
            if (pp[pp[t].a[j]].f != t && pp[pp[t].a[j]].m != t)
            {
                if (pp[pp[t].a[j]].f == -1)
                    pp[pp[t].a[j]].f = t;
                else
                    pp[pp[t].a[j]].m = t;
            }
        }

        scanf("%lld%lld", &pp[t].num, &pp[t].area);
    }

    for (int i = 0; i <= 9999; i++)
    {
        if (h[i])
        {
            if (!vis[i])
            {
                cnt++;
                fam[cnt].minn = 100000;
                fam[cnt].peo = 0;
                fam[cnt].num = 0;
                fam[cnt].area = 0;
                dfs(i);
            }
        }
    }
    printf("%d\n", cnt);
    sort(fam + 1, fam + cnt + 1, cmp);
    for (int i = 1; i <= cnt; i++)
    {
        printf("%04d %d %.3lf %.3lf\n", fam[i].minn, fam[i].peo, fam[i].num * 1.0 / fam[i].peo, fam[i].area * 1.0 / fam[i].peo);
    }
    return 0;
}

L2-010 排座位 (25 分)（并查集/邻接矩阵）

题目思路

使用邻接矩阵和并查集同时维护朋友圈和死对头关系

因为朋友的朋友还是盆友，则有一个拟序关系（满足自反传递的关系)可用并查集维护

而敌人只是一个直接的关系，可用邻接矩阵

#include <bits/stdc++.h>
using namespace std;
int p[105], gx[105][105];
int find(int x)
{
    if (p[x] != x)
    {
        return p[x] = find(p[x]);
    }
    else
        return x;
}
void merge(int a, int b)
{
    int x = find(a);
    int y = find(b);
    if (x != y)
        p[y] = x;
}
int main()
{
    int n, m, k;
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++)
    {
        p[i] = i;
    }
    for (int i = 1; i <= m; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        if (c == -1)
            gx[a][b] = gx[b][a] = -1;
        if (c == 1)
            merge(a, b);
    }
    for (int i = 1; i <= k; i++)
    {
        int a, b, x, y;
        cin >> a >> b;
        x = find(a);
        y = find(b);
        if (x == y && gx[a][b] != -1)
            cout << "No problem" << endl;
        if (x != y && gx[a][b] != -1)
        {
            cout << "OK" << endl;
        }
        if (x == y && gx[a][b] == -1)
        {
            cout << "OK but..." << endl;
        }
        if (x != y && gx[a][b] == -1)
        {
            cout << "No way" << endl;
        }
    }
    return 0;
}

L2-008 最长对称子串 (25 分)（双指针)

L2-008 最长对称子串 (25 分)

对给定的字符串，本题要求你输出最长对称子串的长度。例如，给定Is PAT&TAP symmetric?，最长对称子串为s PAT&TAP s，于是你应该输出11。

输入格式：

输入在一行中给出长度不超过1000的非空字符串。

输出格式：

在一行中输出最长对称子串的长度。

输入样例：

Is PAT&TAP symmetric?

输出样例：

11

看样例思考一会得到可以遍历每一个字符向两边判断是否是对称,分类讨论子串长度是偶数与奇数的情况

时间复杂度:\(O(n^2)\)

反思：在得到解题直觉时不妨多斟酌一下是否可行，考虑是否遗漏其他情况，第一次WA是因为忘记考虑子串长度是偶数情况

#include <bits/stdc++.h>
using namespace std;
string s;
int main()
{
    int maxx = 1;
   getline(cin, s);
    for (int i = 0; i < s.size(); i++)
    {
        int j = i, k = i;
        while (j > 0 && k < s.size() - 1 && s[j] == s[k])
        {
            j--, k++;
        }
        if (s[j] != s[k])
        {
            j++, k--;
        }
        maxx = max(maxx, k - j + 1);
    }
    
    for (int i = 0; i < s.size()-1; i++)
    {
            int j = i, k = i+1;
        while (j > 0 && k < s.size() - 1 && s[j] == s[k])
        {
            j--, k++;
        }
        if (s[j] != s[k])
        {
            j++, k--;
        }
        maxx = max(maxx, k - j + 1);
        
    }
    cout << maxx << endl;
    return 0;
}

L2-013 红色警报 (25 分)(并查集/dfs暴力)

并查集

逆向：逆向读攻城编号

判定关节点方式：去边后连通块增量

邻接表读入边，攻下的城市序号记录并且标记，逆向读攻城编号，当前未被标记的点的相关边才能被采用并merge(),使用ans[]数组记录当前连通块情况，k2,k1为merge后前的连通块数量，若k2<k1-1（即有非被攻下的城市的连通块被连成一块)则该城市并是关节点，否则不是，ans[i]记录是否是关节点情况，并按照这个正序输出语句，若攻下城市总数量等于n则Game Over.

#include <bits/stdc++.h>
using namespace std;
int a[505], p[505], cnt, mark[5005], kk[5005], ans[5005];
vector<int> v[505];
void init(int n)
{
    for (int i = 0; i < n; i++)
    {
        p[i] = i;
    }
}
int find(int x)
{
    if (p[x] != x)
        return p[x] = find(p[x]);
    else
        return x;
}
void merge(int a, int b)
{
    int x = find(a);
    int y = find(b);
    if (x != y)
    {
        p[y] = x;
    }
}
int check(int n)
{
    int c = 0;
    for (int i = 0; i < n; i++)
    {
        if (p[i] == i)
            c++;
        // cout << p[i] << ' ';
    }
    // cout << endl;
    return c;
}
// void merge(int x,int )
int main()
{
    int n, m, k;
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int t, t2;
        cin >> t >> t2;
        v[t].push_back(t2);
        v[t2].push_back(t);
    }
    init(n);
    cin >> k;
    for (int i = 1; i <= k; i++)
    {
        cin >> kk[i];
        mark[kk[i]] = 1;
    }

    for (int i = 0; i < n; i++)
    {
        if (!mark[i])
        {
            for (int j = 0; j < v[i].size(); j++)
            {
                if (!mark[v[i][j]])
                {
                    merge(v[i][j], i);
                }
            }
        }
    }

    cnt = check(n);
    for (int i = k; i >= 1; i--)
    {
        int t = kk[i], last = cnt;
        for (int j = 0; j < v[t].size(); j++)
        {
            if (!mark[v[t][j]])
            {
                merge(v[t][j], t);
            }
        }

        cnt = check(n);
        mark[kk[i]] = 0;

        if (cnt < last - 1)
        {
            ans[i] = 1;
        }
    }
    for (int i = 1; i <= k; i++)
    {
        if (ans[i] == 1)
        {
            printf("Red Alert: City %d is lost!\n", kk[i]);
        }

        if (ans[i] == 0)
        {
            printf("City %d is lost.\n", kk[i]);
        }

        if (i == n)
            printf("Game Over.\n");
    }
    return 0;
}

dfs暴力

判定关节点方式同上

每次重新建立并查集，但是不merge()当前已经被攻下的城市，判定对比连通块数量是否k2<=k1+1（有不是被攻下的城市被分割成新的连通块),若是则不是关节点，否则是。更新k1。

Tarjan直接求关节点其实也可以，不过我不会（