Tire字典树

Tire

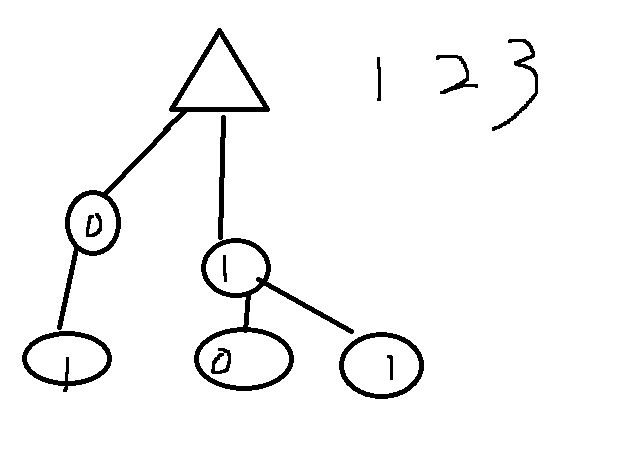
图为插入 1 2 3二进制的Tire字典树

概念：Tire字典树是一种存储字符的数据结构，可用于统计字符串，也可处理字符串之间的关系

字符包括数字等有字符性质的数据

构造（插入）：有序地遍历字符串，从根节点开始查询树中是否有字符串当前字符a[i]

若有则从该字符向子树继续查询，若无则插入该字符作为新节点

（统计字符串时，对每个末尾打上cnt标记，实现统计功能时若插入完成后末尾节点cnt++)

查询：从根节点开始查询，对字符串有序遍历查询字符

若有该字符则从该字符向子树继续查询，直到字符串所有字符都查询成功返回末尾节点cnt为字符串出现次数

若过程中某个字符串查询失败则直接返回0

Tire字典树的应用

ACW143 最大异或对

思路：将所有数字按照31位二进制插入（取决于输入范围，最大的二进制位数31；若最大数x<2^n / 2^n<=x<2(n+1) 则需要从1开始计数的n / n+1位数,），每一位算一层后进行查询，求最大异或对

剪枝：则可以只走当前”层次“可以得到异或结果1的子树，异或结果为0的子树必然小于结果1的子树

划分：

若当前字符有2个分支，则必然有一个子树下一位能得到异或结果1，则转移至该字符

若当前字符有1个分支，且能够得到异或结果1，则转移至该字符

若当前字符有1个分支，不能得到异或结果1，仍然转移至该字符，继续进行查询

#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN (3200005)
using namespace std;
int a[MAXN][2],idx,b[MAXN];
long long maxx=-1;
void insert(int now)
{
    
    int p=0,t=now;
    for (int i = 30; i>=0; i-- )
    {
        int  num=(t>>i)&1;
        if(!a[p][num])
        a[p][num]=++idx;
        p=a[p][num];
    }
}
void query(int b)
{
    int p=0,t=b;
    long long ans=0;
    for (int i = 30; i>=0; i-- )
    {
        
    int num=(t>>i)&1;
    ans<<=1;
    if(a[p][1-num])
    {
    ans=ans|1;
    p=a[p][1-num];
    }
    else
    {
        p=a[p][num];
    }
    
    }
    maxx=max(maxx,ans);
}
int main()
{
    int n;
    cin>>n;
    for (int i = 1; i <= n; i ++ )
    {
     scanf("%d", &b[i]);
     insert(b[i]);
    }
      for (int i = 1; i <= n; i ++ )
      {
          query(b[i]);
      }
      cout << maxx<<endl;
    return 0;
}