差分与前缀和|双指针算法|离散化|单调队列

差分与前缀和

差分与前缀和的关系

ps：图片来源网络，内容自己原创的
这个是图片来源：
https://blog.csdn.net/Sommer001/article/details/121019319

设 An，Bn，Cn三个数组

An差分得到An的差分数组Bn
An求前缀和得到An前缀和数组Cn

1.差分与前缀和互为逆运算

Bn--->(前缀和)An--->(前缀和)Cn

Bn<---(差分)An<---(差分)Cn

2.二维差分与前缀和的公式

推导前缀和的式子
将b单独移到一边得到推导差分的式子
b是a的差分
通用于原数组（b)与前缀和(a)，差分(b)与原数组(a)中前缀和/原数组的推导

区间操作

由当前已求得的前缀和和原数组元素推出新前缀和

1.区间求和（一维）

模板

#include <bits/stdc++.h>
#define MAXN 100005
using namespace std;
int a[MAXN], m, n,s[MAXN];
int main()
{
     cin>>n>>m;
     for(int i=1;i<=n;i++)
     {
         cin>>a[i];
         s[i]=a[i]+s[i-1];
     }
     for(int i=1;i<=m;i++)
     {
         int l,r;
         scanf("%d%d",&l,&r);
         printf("%d\n",s[r]-s[l-1]);
     }

return 0;
}

2.区间求和（二维）

①初始化前缀和

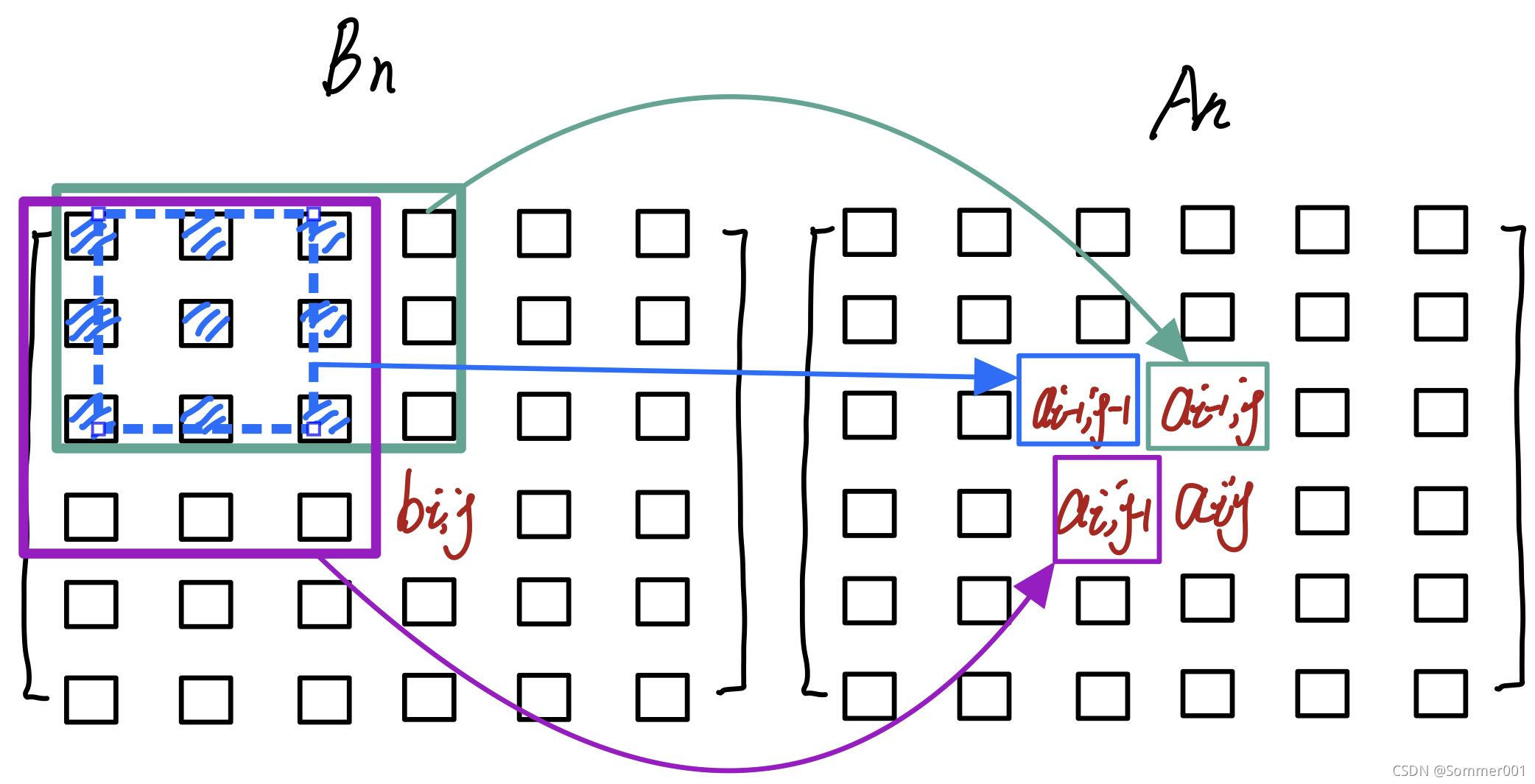
该图左图求a_i_j，由差分求原数组，也可看做由原数组求前缀和，其中b_ij为原数组该位置的元素，a_i-1_j,a_i_j-1,都是该位置上差分数组和的结果和简化

②区间求和公式

\[x_1,y_1,x_2,y_2区间的和\\ s[x_2][y_2]-s[x_2][y_1-1]-s[x_1-1][y_2]+s[x_1-1][y_1-1] \]

解释：将s [x_2] [y_2]部分减去两个区域后由于多减一次再加上多减的部分

#include<bits/stdc++.h>
#define MAXN 1005
using namespace std;
int a[MAXN][MAXN],s[MAXN][MAXN];
int sum(int x,int y)
{
    s[x][y]=s[x-1][y]+s[x][y-1]+a[x][y]-s[x-1][y-1];//求前缀和
}
int cal(int x1,int y1,int x2,int y2)
{
    
    return s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];//求区间求和
}
int main()
{
    int n,m,q;
    cin >> n>>m>>q;
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    {
        scanf("%d",&a[i][j]);
      sum(i,j);
    }
    for(int i=1;i<=q;i++)
    {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
    printf("%d\n",cal(x1,y1,x2,y2));    
    }
    return 0;
}

区间更新求结果

更新差分数组将单个修改时间复杂度优化成O（1）

通过对差分数组求前缀求得结果

1.区间更新（一维）

#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 100005
using namespace std;
int d[MAXN],a[MAXN];
int main()
{
     int n,m;
     cin>>n>>m;
     cin>>a[1];
     d[1]=a[1];
     for(int i=2;i<=n;i++)
     {
         cin>>a[i];
         d[i]=a[i]-a[i-1];//求差分数组
     }
     for(int i=1;i<=m;i++)
     {
         int l,r,c;
         cin>>l>>r>>c;
         d[l]+=c;//对区间开头+c，意为着i>=l之后的原数组都+c，因为得到这些数求和时都加了d[l]
         d[r+1]-=c;//i>=r+1的原数组-c
         		//i>=l&&i<r+1的原数组+c
     }
     
     a[1]=d[1];
     cout<<a[1]<<' ';
     for(int i=2;i<=n;i++)
     {
        a[i]=a[i-1]+d[i];
        cout<<a[i]<<' ';
     }
     
    return 0;
}

2.区间更新（二维）
①更新

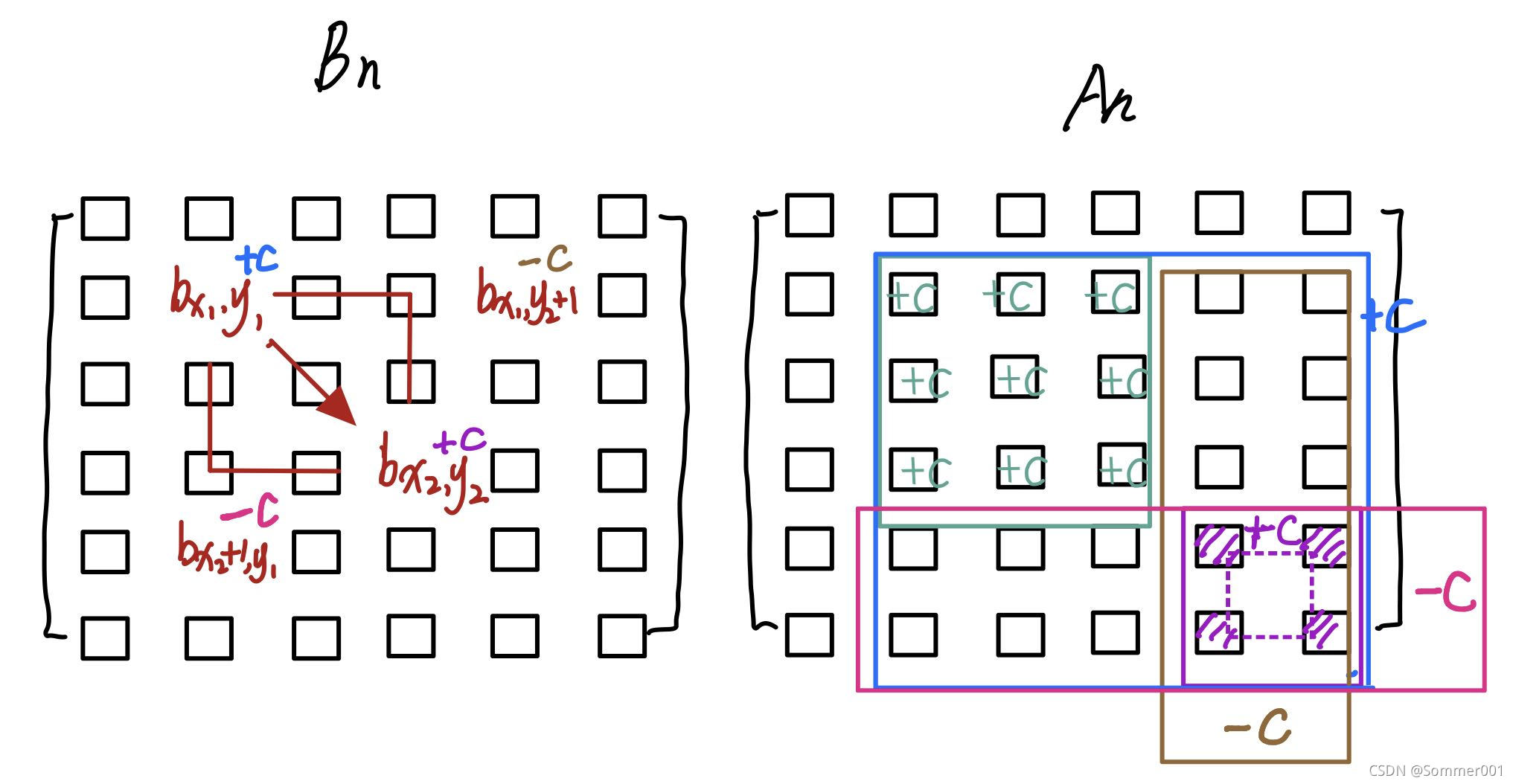
由于b是差分数组，a_i0j0是由所有1=<i<=i0,1<=j<=j0的b数组元素相加得到，则修改b_i0j0值会改变所有i0=<i<=n,j0<=j<=m的a数组元素的值（如图）
则为了删去正方形中如图的两个“长方形”，然后加上小正方形，就要对差分数组的b_{i1}{j1}+c,b{j2+1}+c,b{y1}-c,b_{y2+1}-1，
②求和
按照上面所给的公式求和

#include<bits/stdc++.h>
#define MAXN 1005
using namespace std;

int a[MAXN][MAXN],b[MAXN][MAXN];
void oper(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
    
}
int  cal(int x,int y)
{
    int t=0;
     if(x>1)//防止越界
     t+=a[x-1][y];
     if(y>1)
     t+=a[x][y-1];
     if(x>1&&y>1)
     t-=a[x-1][y-1];
    return  a[x][y]=b[x][y]+t;
    
}
int main()
{
    int n,m,q;
    scanf("%d%d%d", &n,&m,&q);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    {
        int x;
       scanf("%d", &x);
        oper(i,j,i,j,x);
    }

    for(int i=1;i<=q;i++)
    {
        int x1,y1,x2,y2,c;
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
           oper(x1,y1,x2,y2,c);
         
    }
    for(int i=1;i<=n;i++)
    {
    for(int j=1;j<=m;j++)
    printf("%d ",cal(i,j));
    printf("\n");
        
    }
    
    return 0;
}

双指针算法

用途:通过运用特殊性质优化具有“单调性”的暴力循环

大致两种

指向不同序列
指向相同序列，维护一段区间

单调性解释:

例子1. 求最长不重复区间（下称为区间），维护元素区间，若该区间以a[j-1]结尾的区间为a[i~(j-1)],则以a[j]元素作为区间结尾的区间，其左端不小于i，因为若小于i，则最大区间左端不是i，因此j移动过程中i不会往回走，所以是”单调的“
例子2. 数组元素的目标和，a[i]+b[j]>=x题中，因为i>i0时的a[i]>a[i0]，a[i0]+b[j0]>x,则(i>i0 j>j0)a[i]+b[j]>x，则i在向右移动的时候，j只能往左移动，先筛出a[i]+b[j]=<x的临界值，然后再将i右移，此时的j不能右移，因为a[i-1]+b[j]已经>x，a[i]>a[i-1],a[i]+b[j]不可能<=x

优化解释：

例子1.i不会回移，则可以将时间复杂度降为O(n),只遍历大约两遍的数组，可以优化原暴力解中的多次左端点从开头开始循环，再加上使用哈希表和while循环求维护区间内的元素的出现次数，可以将判断是否重复的复杂度降为O(1)

例子2.j只需要左移一遍，可以优化原暴力解中多次遍历b数组的情况

时间复杂度O(n+m)

#include<bits/stdc++.h>
using namespace std;
int a[100005], n, l=1,r=1,maxx=1;
int s[100005];
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        ++s[a[i]];
        while(s[a[i]]>1)
        {
            --s[a[l]];
            l++;
            
        }
        maxx=max(maxx,i-l+1);
    }
    cout << maxx<<endl;
    return 0;
}

#include <bits/stdc++.h>
#define MAXN 100005
using namespace std;
int a[MAXN], b[MAXN];
int main()
{
  
    int n, m, x,l=0,r;
    cin >> n >> m >> x;
    r=m-1;
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    for (int i = 0; i < m; i++)
    {
        cin >> b[i];
    }
    
    for(int i=0;i<n;i++)
    {
         while(r>=1&&b[r]+a[i]>x)r--;
         if(b[r]+a[i]==x)
         {
             cout << i<<" "<<r<<endl;
             break;
         }
    }
    
    
    return 0;
}

离散化

将单调离散的数字按照单调连续的顺序排序

如：

1 25 66 70 1000

1 2 3 4 5

第一行数据存到以第二行为下标的数组中

1.结构体排序

先用结构体数组存储，存储原id和原数据，对结构体以原id增序排序得新id

2.二分查找单调

通过原id查离散后的id是通过二分查找的方式，因为原id随着新id增长而单调递增，二分每次比较离散后id的结构体变量中保存的原id数据

#include <bits/stdc++.h>
int a[100005], sum[100005], countn;
using namespace std;
struct s
{
    int val, id;
} p[100005];
bool cmp(s a, s b)
{
    return a.id < b.id;
}//本题查询原id区间[l,r]之和，而离散化后有原id重复的变量，二分时求原id等于l的最左变量下标，原id等于r的最右变量下标，以解决此问题
int bs(int l, int r, int id)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (p[mid].id == id)
        {
            r = mid;
        }
        if (p[mid].id > id)
            r = mid;
        if (p[mid].id < id)
            l = mid + 1;
    }
    return l;
}
int bs2(int l, int r, int id)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (p[mid].id == id)
        {
            l = mid;
        }
        if (p[mid].id > id)
            r = mid - 1;
        if (p[mid].id < id)
            l = mid;
    }
    return l;
}
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &p[i].id, &p[i].val);

    sort(p + 1, p + 1 + n, cmp);
    for (int i = 1; i <= n; i++)
        sum[i] = sum[i - 1] + p[i].val;
    for (int i = 1; i <= m; i++)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        //要求的区间与有输入值的区间的关系分为五种，下面是[l,r]在区间左边之外和右边之外的情况，和为0
        if (l > p[n].id || r < p[1].id)
        {
            printf("0\n");
            continue;
        }
        int ll = bs(1, n, l);
        int rr = bs2(1, n, r);
        //剩下三种都可以通过二分得到边界
        //要求区间若有一边超过有输入值的区间，则此边会二分得边界点1或n而，而在区间内但查不到的会查到[l,r]内的最近点，即l点查不到查到l右边最近点，这样算出来的区间和才正确，若在l左边则可能加上不该加的值
        printf("%d\n", sum[rr] - sum[ll - 1]);
        // printf("%d  %d\n", rr, ll);
    }

    return 0;
}

单调队列

单调队列求最值

思想：

1.固定“窗口”移动时的最值存在关系，可以从前一个位置的单调队列变化得到

2.单调队列求最小值

若a[i]>a[j],(i<j)，则a[i]在a[j]存在期间不能成为最小值，因此可以从区间里去掉a[i],从而下标比j小的“窗口”中的值都小于a[j],得到单调递增的队列

#include<bits/stdc++.h>
#define MAXN 1000005
using namespace std;
int a[MAXN],q[MAXN],head=1,tail=1;//[head,tail)队列范围
//q存储下标
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    
    for(int i=1;i<=n;i++)
    {
    while(head<tail&&a[q[tail-1]]>a[i])//若尾元素比当前要插入的大，破坏单调递增，无法成为之后最小值的元素需删除
        tail--;
    q[tail++]=i;
    if(head<tail&&q[head]<i-k+1) head++;//需要保持窗口大小k，下标超出范围的不符合条件
    
    if(i>=k) printf("%d ",a[q[head]]);//需要判断的是k大小窗口的最小值，因此需要插入过的元素达到k个时输出，否则不是需要判断的是k大小窗口的最小值
    
    }
    //下面是求最大值，主要是大于小于符号变化了
    printf("\n");
    head=1,tail=1;
    for(int i=1;i<=n;i++)
    {
    while(head<tail&&a[q[tail-1]]<a[i])
        tail--;
        
    q[tail++]=i;
    
    if(head<tail&&q[head]<i-k+1) head++;
    
    if(i>=k) printf("%d ",a[q[head]]);

    }
    
    return 0;
}

相似的还有单调栈

#include <iostream>
#include <cstring>
#include <algorithm>
#include<stack>
using namespace std;
int a[100005];
stack<int>st ;
int main()
{
    int n;
    cin>>n;
    st.push(-1);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d",&a[i]);
    while (st.top()>=a[i])
    st.pop();
        printf("%d ",st.top());
    st.push(a[i]);
    }
    return 0;
}

posted @ 2022-01-12 23:01 多巴胺不耐受仿生人阅读(66) 评论(0) 收藏举报

刷新页面返回顶部

多巴胺不耐受仿生人

差分与前缀和|双指针算法|离散化|单调队列